---

理想気体の状態方程式

---

• 「気体」というものの特徴
  • 分子が十分に大きな運動エネルギーを持っているために、広い空間を、大きな速度で移動している。
    したがって、分子同士が接近する可能性は極めて小さいと考えてよい。
    分子間力はさまざまな要因で生じるが、その本質は、「静電引力」である。静電引力は距離の2乗に反比例する（逆2乗法則）。だから、分子同士がよほど接近しないかぎりその影響は無視できる。
  • 容器の形によって、形を変える。分子のまったくランダムな運動によって、容器の隅々までまったく均等に広がる。
    二種類以上の分子からなる「混合気体」の場合にも、
    1. それぞれの成分気体が、容器の全体積を占め、
    2. かつ、他の気体が存在することの影響を、相互にまったく受けない、
    と考えてよい。
    したがって、「混合気体」の「分圧」は、その容器にその気体が単独で存在したときに示す圧力と、まったく同じと考えられる。(ドルトンの「分圧の法則」)

    成分気体1	成分気体2	混合気体

  • 気体の「圧力」とは、運動する分子が容器の壁面に衝突するときに、壁面に加える力を、その壁面の面積で割ったものである。[Pa=N/m²]
    したがって、「圧力」は、
    1. 分子が壁面に衝突する頻度（確率）が高いほど、
    2. 衝突する分子が大きな運動エネルギーを持っているほど、
    大きくなる。
    熱力学によれば、
    1. 気体の「内部エネルギー」（運動エネルギーの総和にほぼ等しい）は、絶対温度に比例する。
    2. 運動エネルギーは、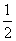mv²、すなわち、速度の2乗に比例する。
    したがって、温度が高いほど、速度は大きくなり、速度が大きいと、
    1. 容器の壁の間を往復して、再び衝突する時間が短くなるから、衝突確率は高くなり、
    2. 衝突の際に壁面に加える力も、大きくなる。
    
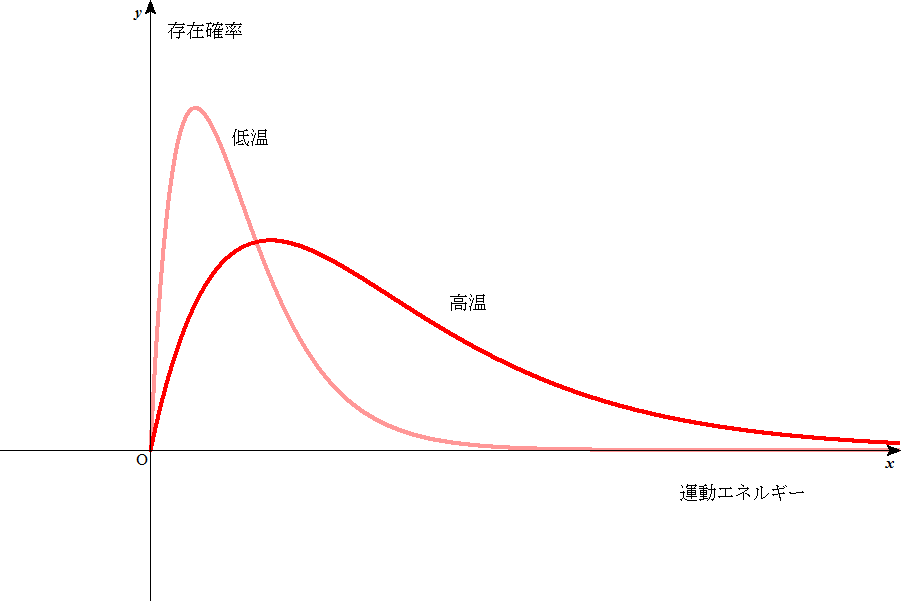
    マックスウェル・ボルツマン分布（気体分子のもつエネルギーの分布）
    
    
• ボイルの法則
  温度が一定の条件の下では、気体の圧力(P)と、体積(V)は、反比例する
• シャルルの法則（シャルル／ゲイ・リュサックの法則）
  圧力一定の条件の下では、気体の占める体積は、温度が1上昇するごとに、0のときの体積の1/273だけ増加する。
  
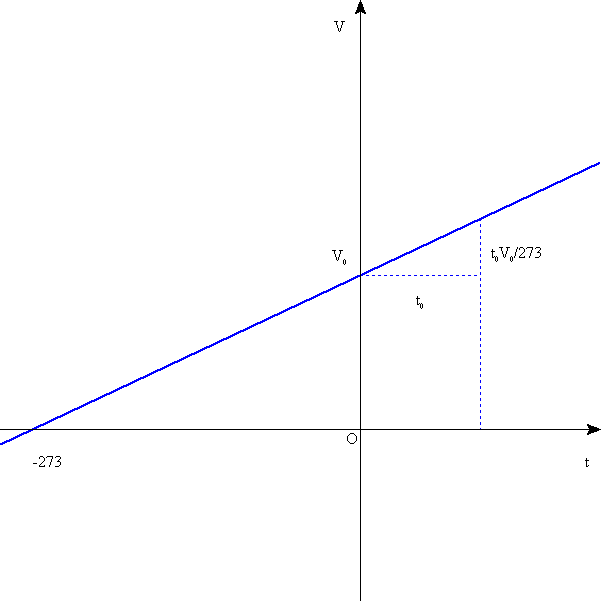
  横軸に「摂氏（セルシウス）温度」、縦軸に体積をとってグラフを描くと、原点を通らない1次関数で、その傾きは0のときの体積をV₀とすると、V₀/273、
  原点を通らない、つまり「比例関係」ではない法則は、何かと不便なので、このグラフが横軸と交わるポイント、すなわち、摂氏マイナス273度を、原点とする新たな座標軸を採用することにした。
  これを「絶対温度」といい、その単位は[K]ケルビン。
  こうして、シャルルの法則は、次のように言い換えることができる。
  圧力一定の条件の下では、気体の体積(V)は、絶対温度(T)に比例する。
• ボイル・シャルルの法則
  上の二つの法則から、当然に、次のように言える。
     （一定）
  
  
• 理想気体とは？
  1. 分子間力を無視する。
  2. 分子自身の大きさを無視する。
• 理想気体の状態方程式
  • 「アボガドロの法則」によれば、「同温、同圧、同体積の気体には、気体の種類にかかわらず、同数の分子が存在する」。
       
    ならば、ボイル・シャルルの法則の右辺のcは、一定量を決めれば、気体の種類にかかわらず定数となるはずである。
  • 質量数12の炭素(¹²₆C)は、ほぼ質量が等しい、6個の陽子と、6個の中性子でできている。
    その質量は、「何か」の12倍のはずだ。そこで、この炭素原子がいったいいくつ集まれば、質量12gとなるかを調べた。
    これが「アボガドロ数」N_A=6×10²³であり、その「アボガドロ数」個の集団を、「モル」molと名付けた。
  • nmolの気体に対して、次の式が成り立つ。
    PV=nRT
    P[Pa]:圧力
    V[L]:体積
    n[mol]:物質量（モル数）
    T[K]:絶対温度
    気体定数:R=8.31×10³

    ---

    0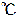すなわち273K、一気圧(1013hPa、1.013×10⁵Pa)で、1molの気体が占める体積は、
    
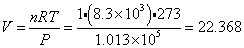
    約22.4Lとなる。
  
  
  
• 実在気体の、理想気体からのずれ
  理想気体とは、
  1. 分子間力を無視する。
  2. 分子自身の大きさを無視する。
  であるから、当然、分子間力も分子自身の大きさもある実在気体では、厳密には状態方程式が成り立たないことになる。その「ずれ」をどう評価すべきだろうか？
  1. 分子間力が無視できない状況とは？
     分子間の距離が非常に小さい、すなわち、非常に狭い空間に分子が押し込められている。
     温度が一定なら、ものすごく高圧、または、圧力一定なら、ものすごく低温という状況であろう。
  2. 分子自身の大きさを無視できない状況とは？
     分子がさらに接近して、ほとんど重なりあいが生じているような状況、きわめて高圧、または、絶対零度に近い超低温。
  ここで「圧縮率因子」Zというものを考える。
  
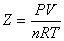
  理想気体であるならば、この値は当然1になるはずである。1より大きくなったり、小さくなったりする要因は何か？
  圧力P、温度T、もちろん物質量n一定で考えると、この値は体積Vに比例する。
  1. Zが1より大きいということは、「体積増加要因」が「体積減少要因」より大きな影響を持っている、
  2. Zが1より小さいということは、「体積減少要因」が「体積増加要因」より大きな影響を持っている、
  といえる。
  1. 本当は分子間力があって、気体分子が引き合っているのに、これを無視したのだから、分子間力の存在は、「体積減少要因」である。
  2. 本当は分子に大きさがあるのに、これを無視したのだから、分子の大きさは、「体積増加要因」である。
  
  
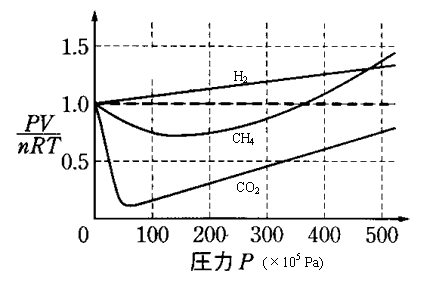
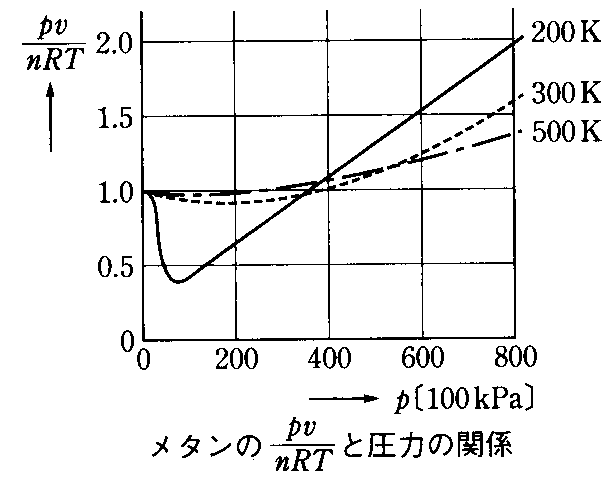
  • 上の左のグラフでは、水素H₂、メタンCH₄、二酸化炭素CO₂の0=273Kでの「圧縮率因子」を比較したものである。
    一般に、分子間力は、極性の大きいものの方が大きく、極性が同じくらいならば、分子量が大きいものほど大きい。
    これら3種の分子はいずれも無極性であり、分子量はH₂=2、CH₄=16、CO₂=44であるから、この順に分子間力が大きくなる。
    圧力が比較的小さいエリアでは、「体積減少」側へのずれていて、中でも分子間力が最も大きい二酸化炭素のずれが激しい。
    しかし、圧力があまりに大きくなると、どの気体も「体積増加」側へずれはじめる。
  • 右のグラフは、同一の気体、メタンCH₄について、温度条件を変えてみた結果である。
    摂氏0度よりも低い200Kのときのみ、大きく「体積減少」側にずれているて、温度が高くなるにつれて、その傾向は小さくなる。。
    しかし、圧力があまりに大きくなると、どの温度条件でも「体積増加」側へずれはじめる。