正の実数x,y,zが
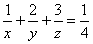
をみたすとき、
x+2y+3zの最小値を求めよ。
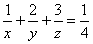
zを、定数z0とみなして、
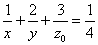
 ・・・(1)
・・・(1)
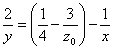
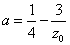 とおくと、a>0
とおくと、a>0
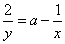
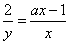
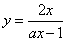
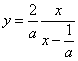
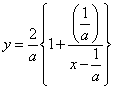
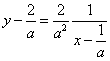 ・・・(1')
・・・(1')

これは、漸近線
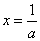 ,
,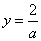
とする分数関数である。
x+2y+3z0=Aとおく。
これは傾き-
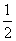 の直線である。
の直線である。
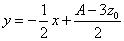 ・・・(2)
・・・(2)

これら(1)(2)が第1象限で、共有点をもつ条件の下で、Aが最小となるのは、両者が接するときであろう。
|
【問題】
正の実数x,y,zが 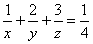
をみたすとき、 x+2y+3zの最小値を求めよ。 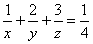
zを、定数z0とみなして、 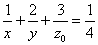
 ・・・(1) ・・・(1)
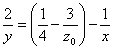
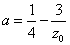 とおくと、a>0 とおくと、a>0
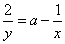
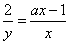
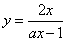
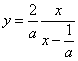
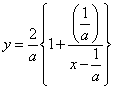
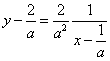 ・・・(1') ・・・(1')
|

これは、漸近線 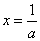 , ,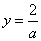 とする分数関数である。 x+2y+3z0=Aとおく。 これは傾き- 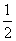 の直線である。 の直線である。
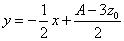 ・・・(2) ・・・(2)

これら(1)(2)が第1象限で、共有点をもつ条件の下で、Aが最小となるのは、両者が接するときであろう。 |
そこで、(1)の微分係数が、-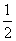 となるような となるような(1)上の点を求めることになる。 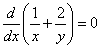
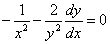
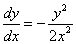
これが、- 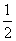 に等しいから、 に等しいから、
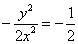
y2-x2=0 (y-x)(y+x)=0 求める点は第1象限にあるから、y=x・・・(3) (1')(3)の交点が、求める接点である。 

(2)にこれを代入して、 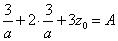
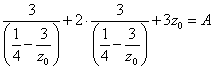
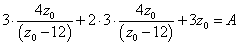
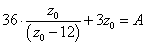

|
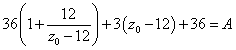
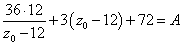
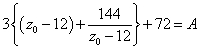
ふたたび、定数z0を変数zと読み直して、 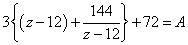
ここで、 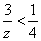 すなわちz>12だから、 すなわちz>12だから、
相加平均・相乗平均の関係より、 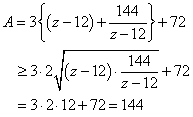
等号が成立するのは、 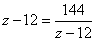
すなわち、 (z-12)2=144 (z-12)2-122=0 {(z-12)-12}{(z-12)+12}=0 z(z-24)=0 z>12だから、z=24 一方、接点は、 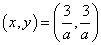 であるから、 であるから、
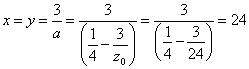
以上から、x=y=z=24のとき、最小値144をとる。 【注】陰関数微分のところは、「判別式」による処理も可能。そうすれば、かつかつ、文系の範囲、とも言えるか? |