1. センターIIB2012本1_2



  3. cos5θ+cos3θ=0  を満たすθを求めよ。


  4. センターIIB2010本1_2




1[IIB2012本1_2]
 1[IIB2012本1_2]
1[IIB2012本1_2]
 1[IIB2012本1_2]

1[IIB2012本1_2]
 1[IIB2012本1_2]
2
 4[IIB2010本1_2]

5
 5
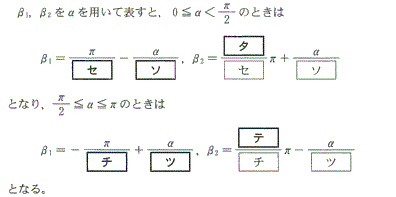
[3]
cosα=cosβを満たすα,βの関係は、
β=α+2nπ   (ただし、nは任意の整数)  
または、
β=-α+2nπ   (ただし、nは任意の整数)  
となる。
cos5θ=-cos3θ
cos5θ=cos(π-3θ)
上の結論から、
5θ=(π-3θ)+2nπ  (ただしnは任意の整数)
または、
5θ=-(π-3θ)+2nπ  (ただしnは任意の整数)
すなわち、
8θ=(2n+1)π  (ただしnは任意の整数)
または、
2θ=(2n-1)π  (ただしnは任意の整数)
もちろん後者は、
2θ=(2n+1)π  (ただしnは任意の整数)
でかまわない。

よって、
θ=(2n+1)π/8  (ただしnは任意の整数)
または、
θ=(2n+1)π/2  (ただしnは任意の整数) 		[別解]
cos5θ+cos3θ=0
2cos4θcosθ=0
cos4θcosθ=0
すなわち、
cos4θ=0または、cosθ=0

4θ=(2n+1)π/2  (ただしnは任意の整数)
または、
θ=(2n+1)π/2  (ただしnは任意の整数)

よって、
θ=(2n+1)π/8  (ただしnは任意の整数)
または、
θ=(2n+1)π/2  (ただしnは任意の整数)