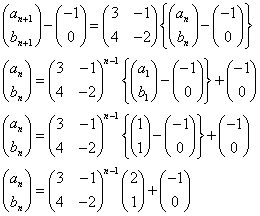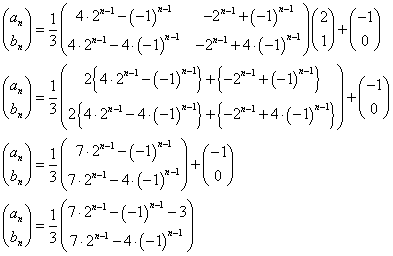• 漸化式
  a_n+1=3a_n-b_n+2      a₁=1
  b_n+1=4a_n-2b_n+4    b₁=1
  
  
  すなわち
  
  を解きたい。

  ---

• まず、
  
  に対して、Aⁿを求める。
  
  
  
  • 「固有値」、「固有ベクトル」を求める。
    
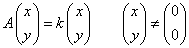
    すなわち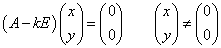
    
    このような列ベクトル(x,y)が存在する必要十分条件は、(A-kE)が逆行列をもたない（非正則である）ことである。
    
    (3-k)(-2-k)-(-1)4=0
    (k-3)(k+2)+4=0
    k²-k-2=0
    (k-2)(k+1)=0
    k=2,-1  (固有値)
    
    
  • k₁=2に対して、
    
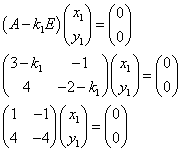
    すなわち、
    x₁-y₁=0
    これをみたすx₁,y₁は無数に存在するが、それらのうち、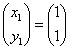
    
    とする。
    
    
  • k₂=-1に対して、
    
    すなわち、
    4x₂-y₂=0
    これをみたすx₂,y₂は無数に存在するが、それらのうち、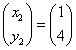
    
    とする。
    
    
  • したがって、
    
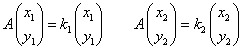
    すなわち、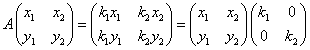
    
    行列P,Bを以下のように定めると、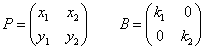
    
    AP=PB
    ここに、固有ベクトル(x₁,y₁),(x₂,y₂)は、互いに1次独立であるから、Pは逆行列P^-1をもつ。
    A=PBP^-1
    したがって、
    Aⁿ=PBⁿP^-1
    
    
    ここで、対角行列Bのn乗は容易に計算できて、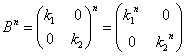
    
    
    
  • 具体的に計算すると、
    
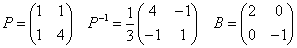
    であるから、
    
  
  
  

  ---

• 次に、
  1. 任意の2次元ベクトルは、1次独立な2個のベクトルの1次結合として一意的に表現できること
  2. 異なる2個の固有値に対応する固有ベクトルは互いに1次独立であること
  から、
  
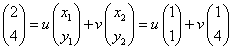
  をみたす(u,v)を一組、定めることができる。
  u+v=2
  u+4v=4
  u=4/3  v=2/3
  
  
• 与えられた漸化式は、
  
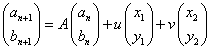
  と書けることになるから、これを次のように変形できれば、
  
  次のように、一般項が得られるであろう。
  
  
  
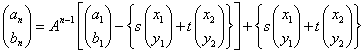
  そこで、このような定数s,tを定めよう。
  
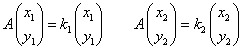
  であるから、
  
  
  
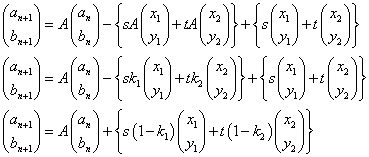
  したがって、
  s(1-k₁)=u    t(1-k₂)=v
  
  
  
• 具体的に計算すると、
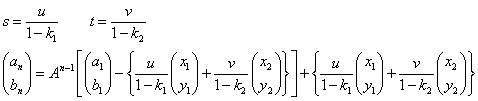
  (a₁,b₁)=(1,1)    (k₁,k₁)=(2,-1)    (x₁,y₁)=(1,1)    (x₂,y₂)=(1,4)
  u=4/3  v=2/3
  であるから、
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  

  ---

• ここでは、「一般解」を得る方法を考えたが、実用的には、単に係数比較を行うだけで、解くことが出来る。
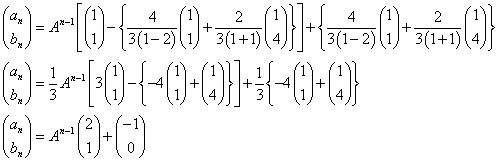
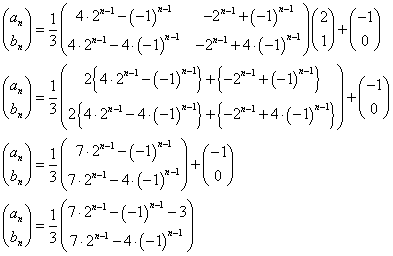
  つまり、次のように列ベクトル(p,q)を仮定して、
  
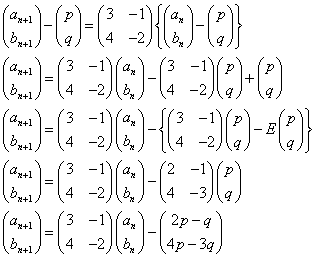
  これを、
  
  と比較し、
  2p-q=-2
  4p-3q=-4
  すなわち、
  
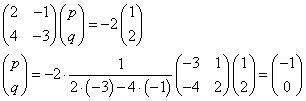
  こうして、同じ結果が得られる。