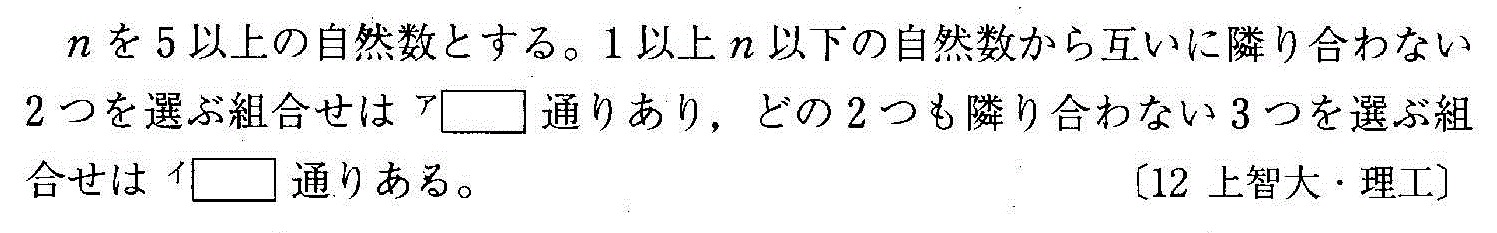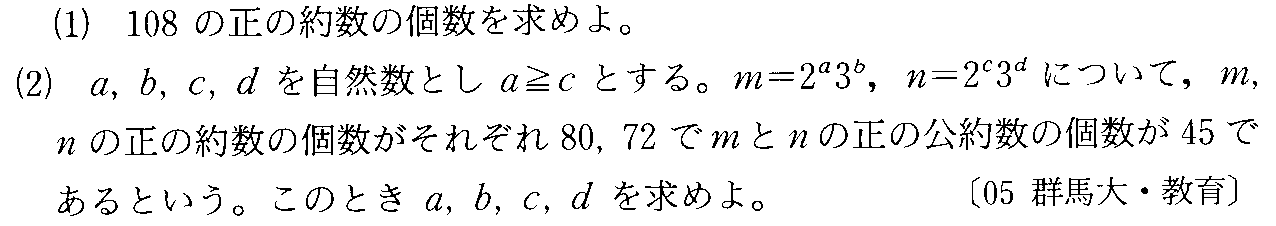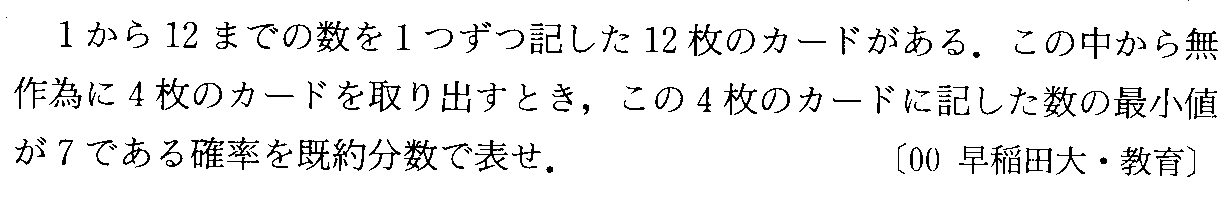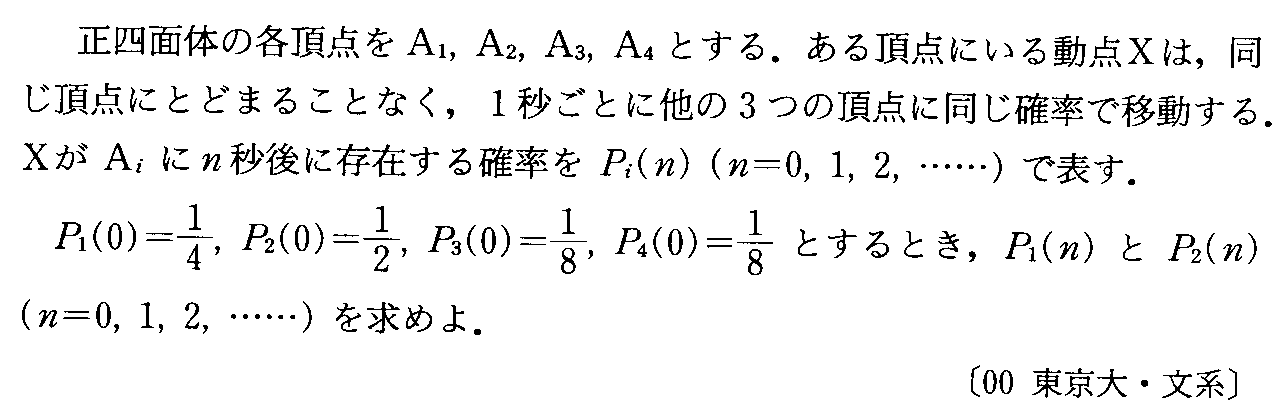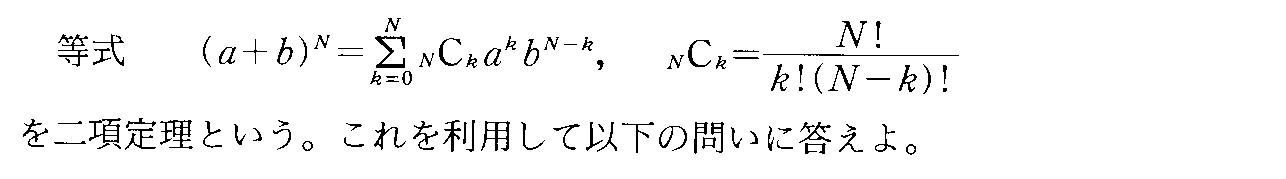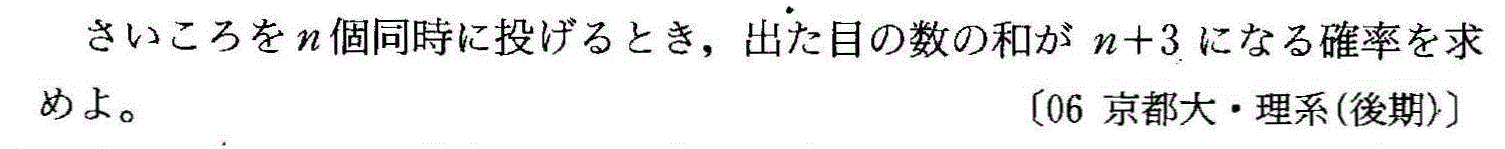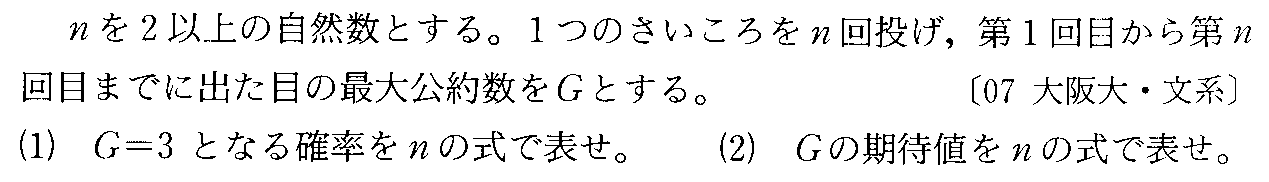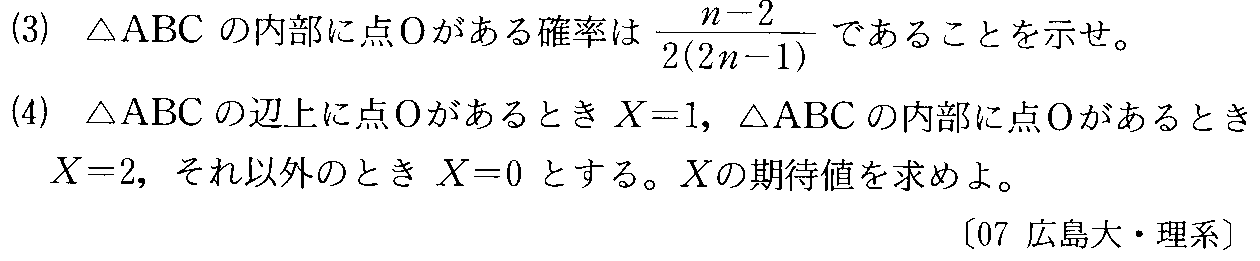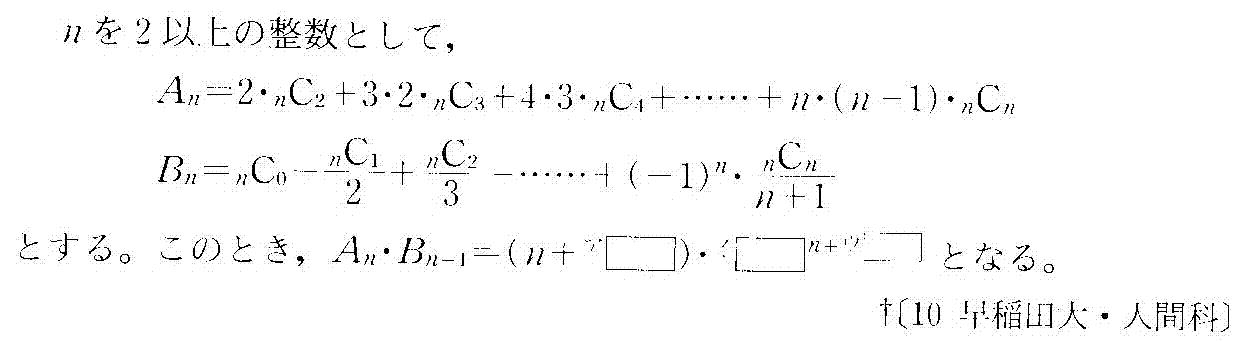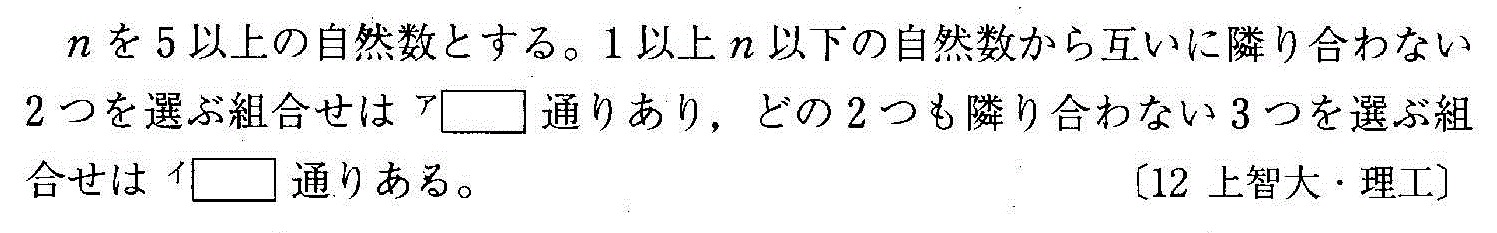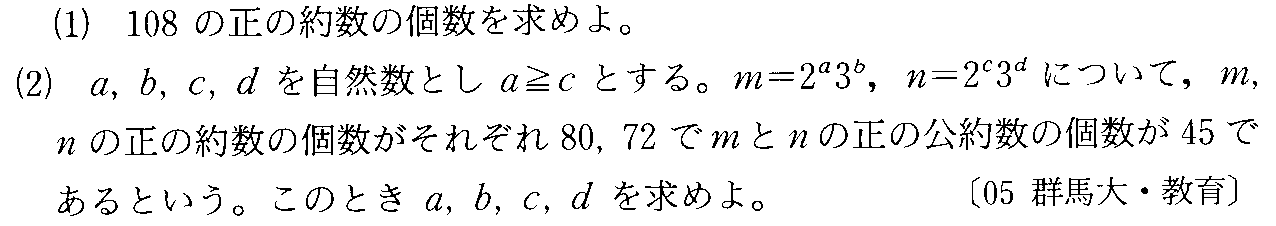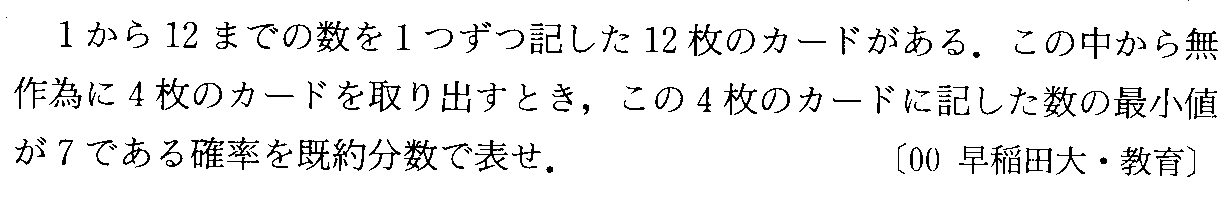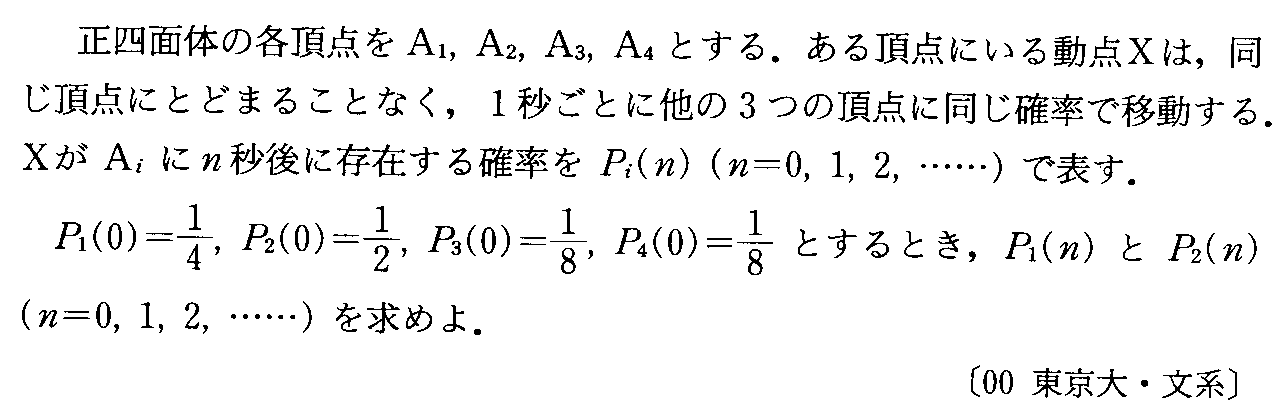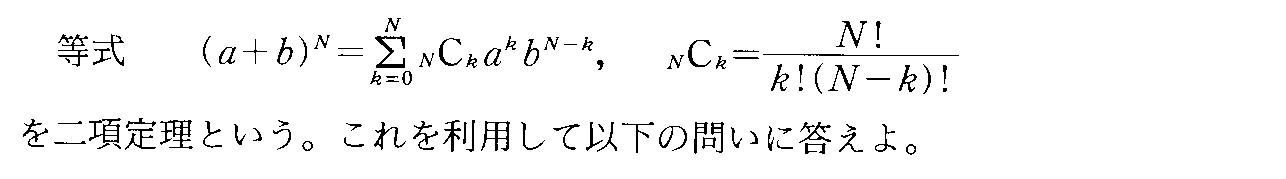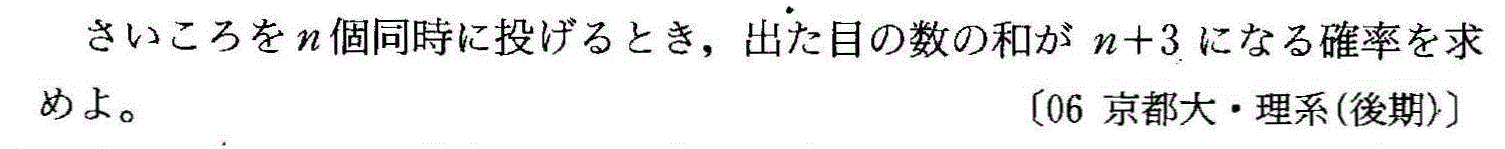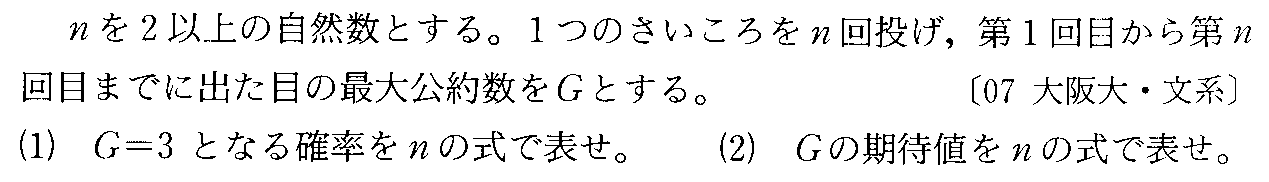場合の数・順列・組み合わせ

  1. [2000b265]*円順列の立体化


  2. [2000b269]円順列・じゅず順列


  3. [2000b255]1次不定方程式・同じものを含む順列


  4. [2002b243]**組み合わせ・二項定理の利用


  5. [2002b244]*区別のつく「もの」を、区別のつかない「容器」に分ける


  6. [2002r245]*区別のつかない「もの」を、区別のつく「容器」に分ける


  7. [2003b232_2]*円順列の立体化


  8. [2003b238]区別のつく「もの」を、区別のつかない「容器」に分ける


  9. [2003r236]**「一対一対応」をつける


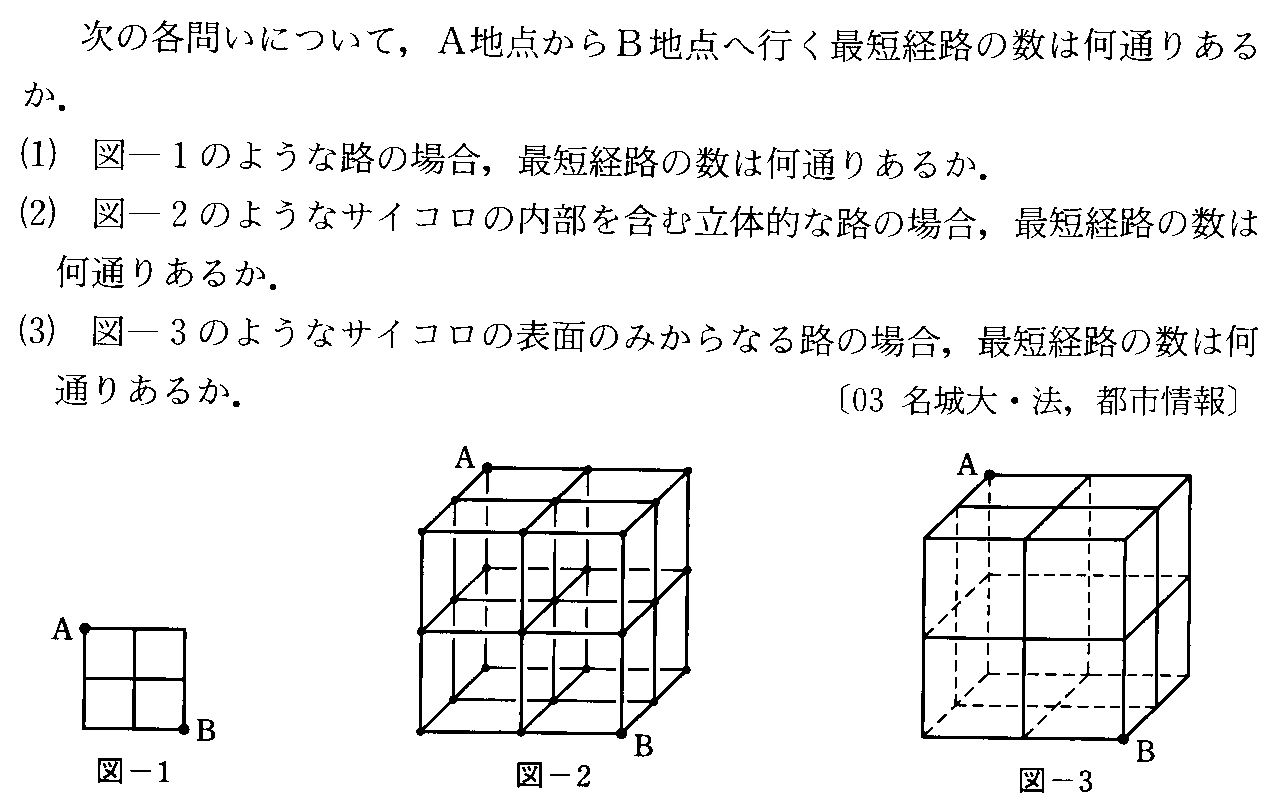
  10. [2003r241]3次元最短経路問題・同じものを含む順列


  11. [2004b241_3]正多角形の頂点を結んで三角形を作る


  12. [2004b246]二項定理の利用・数列の増減は、「階差数列」が教えてくれる


  13. [2004r242_2]*nからn+1への変化を見る


  14. [2005r080]凸多角形の対角線


  15. [2006b078]円順列・じゅず順列


  16. [2006b081]最短経路・同じものを含む順列


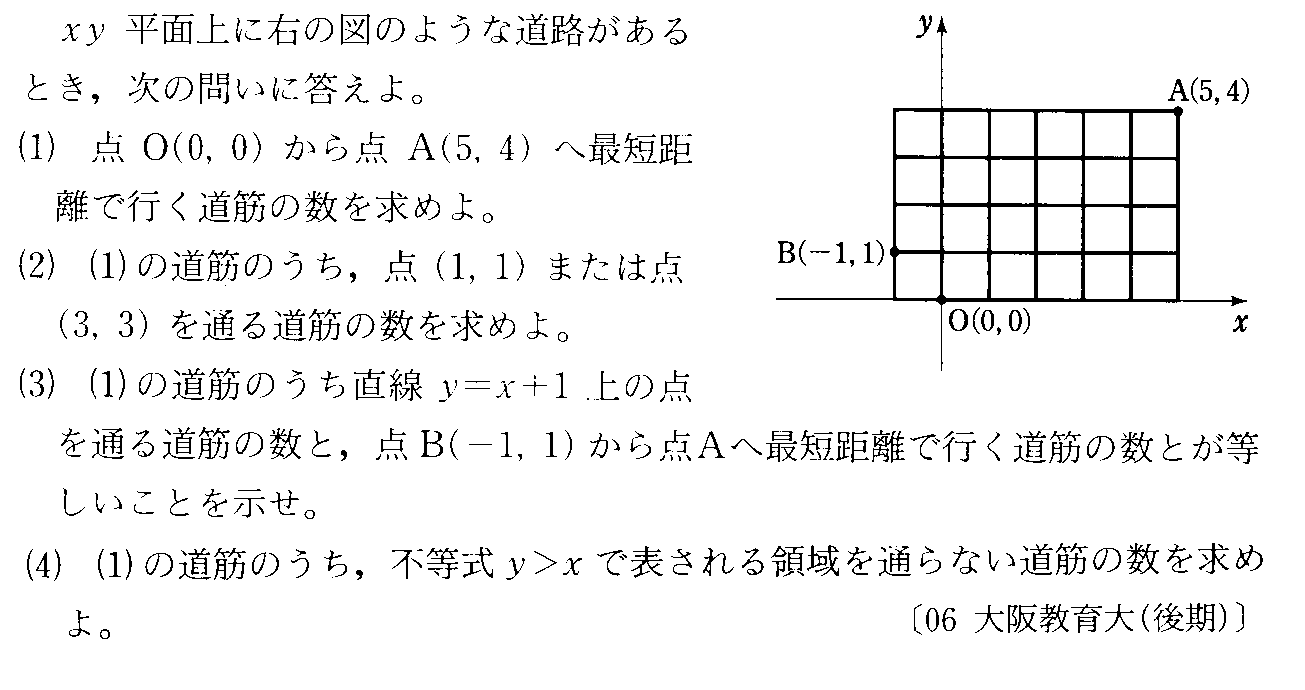
  17. [2006r084]最短経路・同じものを含む順列


  18. [2006r086]*「重複組み合わせ」という考え方・「一対一対応」を発見する


  19. [2007b079]nからn+1への変化を見る


  20. [2007r078]組み合わせ・余事象の利用


  21. [2007r079]*「重複組み合わせ」という考え方・パスカルの三角形


  22. [2008r082]**3次元最短経路問題・同じものを含む順列・包除原理


  23. [2010r079]*3次元最短経路問題・同じものを含む順列・包除原理


  24. [2011b080]**｢重複組み合わせ｣という考え方


  25. [2012b077]*｢重複組み合わせ｣という考え方


  26. [2012r075]直線の交点の個数


  27. [2012r077]同じものを含む順列


  28. [2012r079]小さな自然数から、類推によって「一般化」する


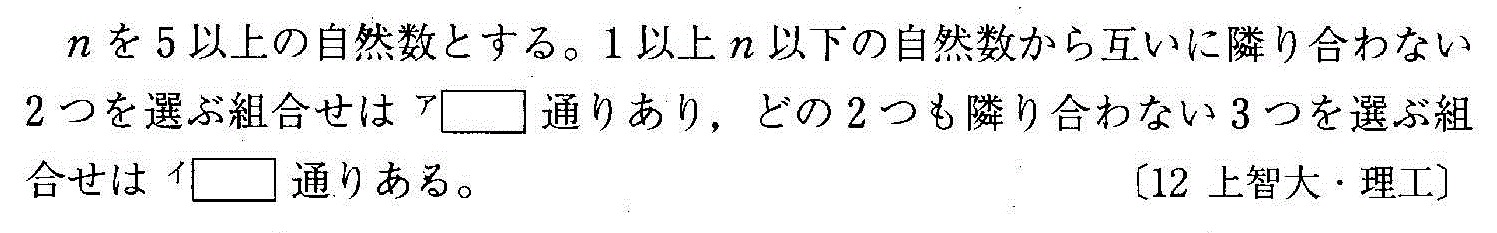
  29. [2012r080]一対一対応を発見する


    集合の要素の個数

  30. [2005r077]約数の個数


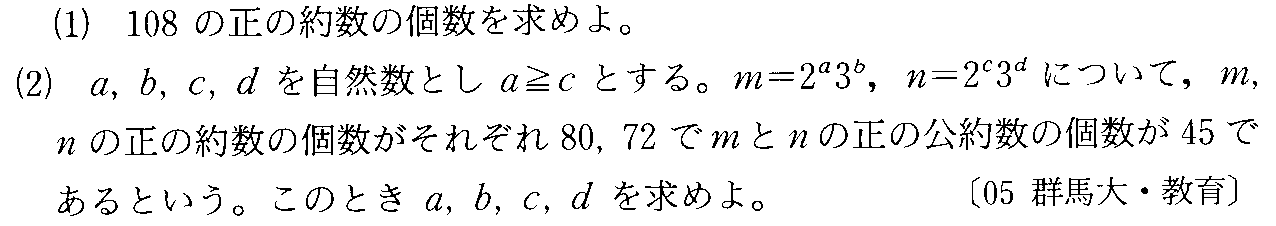
  31. [2009b080]*ものを並べる話にすりかえる・自然数とは端からつけた番号である


  32. [2009b082]*二項定理の応用・n人の旅人が2部屋に泊まる


  33. [2010b075]*素数は｢否定文｣でしか定義できない


    確率

  34. [2000b274_3]取り出す集合を性格の異なるカテゴリーに分類する


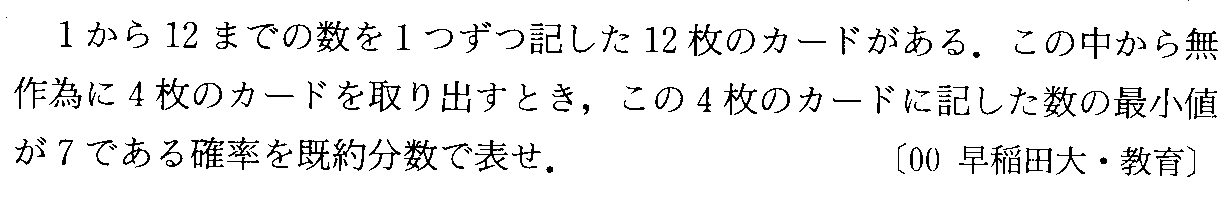
  35. [2000b275]「区別がつく」のか「区別がつかない」のか？、Pなのか？、Cなのか？


  36. [2000b276]取り出す集合を性格の異なるカテゴリーに分類する


  37. [2000b285]包除原理・数学的帰納法


  38. [2000r283]「余事象」の使い方


  39. [2000r291]nからn+1への変化を見る


  40. [2000r293]相互に独立な試行を多数回反復する


  41. [2000r295]相互に独立な試行を多数回反復する


  42. [2000r298]正四面体の頂点移動・n回目に「いる」ならからn+1回目には「いない」


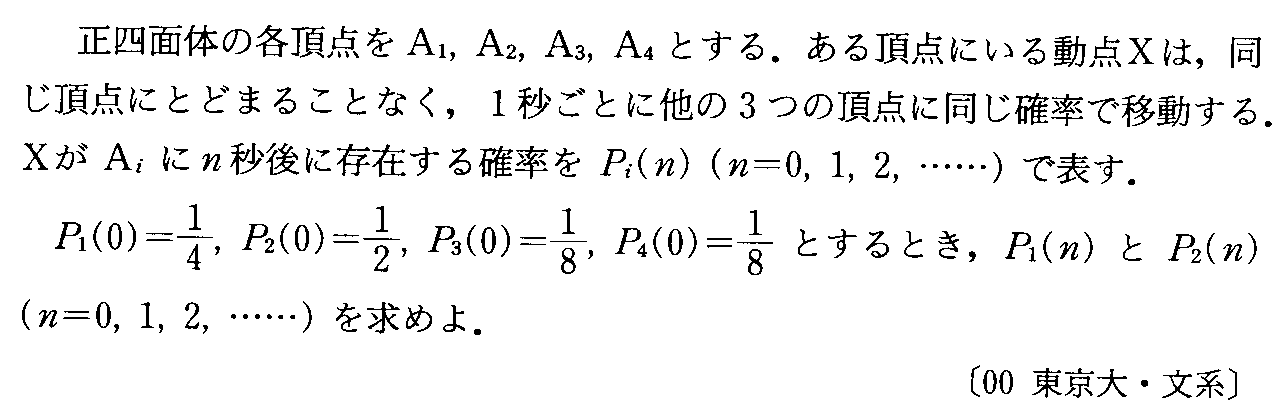
  43. [2000r300]nからn+1への変化を見る・連立漸化式


  44. [2000r304]正多角形の頂点を結んで三角形を作る


  45. [2001b277]相互に独立な試行を多数回反復する・同じものを含む順列


  46. [2001b282]期待値・復元抽出と非復元抽出の違い


  47. [2001b284]期待値・「余事象」の使い方・(「和の期待値」と「期待値の和」)


  48. [2002b258]**「余事象」の使い方


  49. [2002b263]正多角形の頂点を結んで三角形を作る


  50. [2003b246]*勝負が決まったらあとのゲームはしなくてよい、でも、してもよい


  51. [2003b248]数列の増減は、「階差数列」が教えてくれる


  52. [2003b256]**「累積確率(・・・以下である確率)」という考え方


  53. [2003b258]*数直線上の移動を「最短経路」の問題にすりかえる


  54. [2003r249]*数列の増減は、「階差数列」が教えてくれる


  55. [2004b259]*「3人から1人勝ち」と「2人から1人勝ち」では確率が異なる


  56. [2004r248_3]「累積確率(・・・以下である確率)」という考え方


  57. [2004r251]*SnとPnを含む漸化式([2008r099]と同じ)


  58. [2004r267]**連立漸化式


  59. [2004r268]*二項定理を用いた期待値計算


  60. [2005b092]*包除原理


  61. [2005b100](期待値の和と和の期待値)


  62. [2005b105]「選んだ」段階で「順序」は自動的に決まっている？


  63. [2005r088]正多角形の頂点を結んで三角形を作る


  64. [2005r089]凸多角形の対角線


  65. [2005r096]二項定理の利用




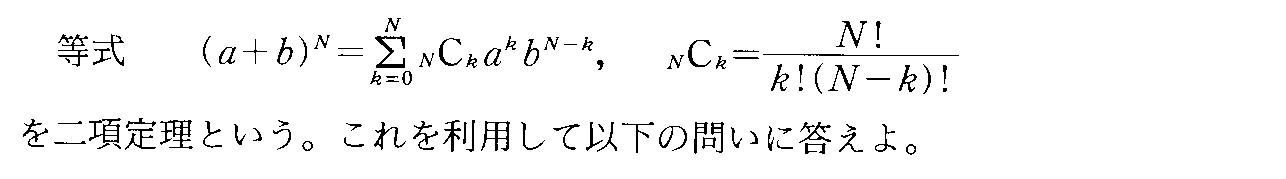
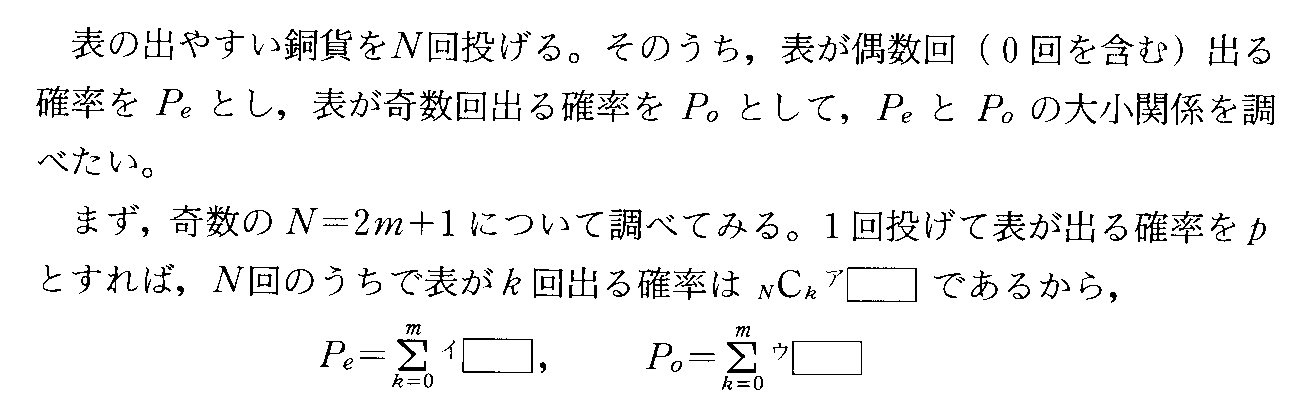
  66. [2005r097]「先攻」が有利なのか？


  67. [2005r105]期待値・2次関数の最大値


  68. [2005r106]**二項定理を用いた期待値計算


  69. [2006b096]*小さな自然数から、類推によって「一般化」する


  70. [2006b098]**「重複組み合わせ」という考え方・包除原理


  71. [2006b099]数列の増減は、「階差数列」が教えてくれる


  72. [2006b101]nからn+1への変化を見る・漸化式


  73. [2006r091]確率が「推計学」に応用される場面


  74. [2006r093]*「重複組み合わせ」という考え方


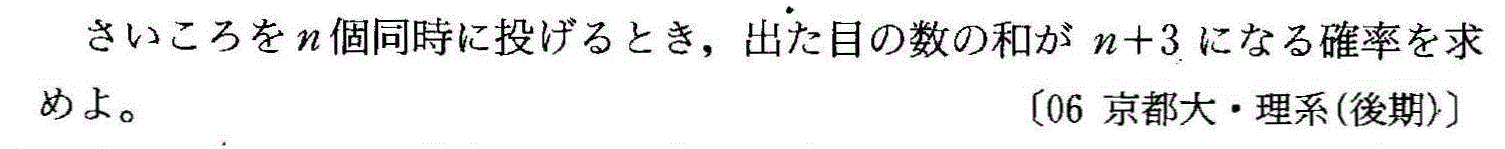
  75. [2006r096]*「同値関係」の証明・整数には偶数か奇数か、どちらかしかない


  76. [2006r099]3次元経路問題・同じものを含む順列


  77. [2006r102]いびつなサイコロ・漸化式


  78. [2006r106](回転行列の利用)・漸化式


  79. [2006r109]等比数列的な増殖・漸化式


  80. [2007b088]pkがkの2次式になるとき([2008r094]と同じ)


  81. [2007b089]和がとりうる値、積がとりうる値


  82. [2007b092]*等確率でない試行を繰り返すと世界に偏りが生じるという話


  83. [2007b093]サンプルが増えると、誤差が大きくなってしまうという話


  84. [2007b094]*四角錐だから、頂点Oだけが非対称だ


  85. [2007b096]*引かれるくじの立場で考える（期待値の和と和の期待値）


  86. [2007b099]*包除原理


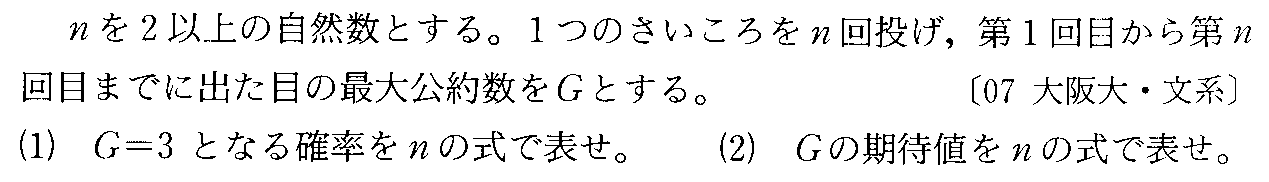
  87. [2007r101]*小さな自然数から、類推によって「一般化」する


  88. [2007r105]正多角形の頂点を結んで三角形を作る



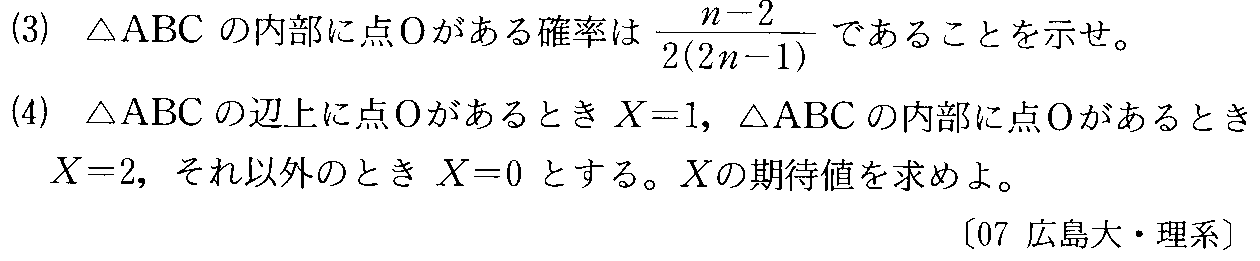
  89. [2007r106]相互に独立な試行を多数回反復する


  90. [2008b087]包除原理


  91. [2008b088]順序を問題にする


  92. [2008b090]数列の増減は、「階差数列」が教えてくれる・全事象は何かと考える


  93. [2008b093]包除原理


  94. [2008b097]**数直線上の移動を「最短経路」の問題にすりかえる


  95. [2008b098]**連立漸化式・どちらにしかいないのだから、その和は1だ


  96. [2008b104]競技の途中で競技者の確率論的判断が関与する場合


  97. [2008r094]*「累積確率(・・・以下である確率)」という考え方([2007b088]と同じ)


  98. [2008r099]**SnとPnを含む漸化式([2004r251]と同じ)


  99. [2008r100]**包除原理(「少なくとも1回」の処理)


  100. [2008r107]小さな自然数から、類推によって「一般化」する


  101. [2009b085]包除原理


  102. [2009b086]余事象を考える・具体的な数値を代入して検討する


  103. [2009b091]｢じゃんけん｣の公平性について考えさせられる


  104. [2009b093]**正四面体の頂点を移動する・漸化式・どこかにかならずいるから合計は1


  105. [2009b095]漸化式([2009r096]に含まれる)


  106. [2009b096]*小さな自然数から、類推によって「一般化」する


  107. [2009b099]すべての場合を列挙する


  108. [2009b101]競技者に｢優劣｣が設定されているから、複雑な値になる


  109. [2009r096]**漸化式([2009b095]を含む)


  110. [2009r098]*偶数と奇数で形が異なる漸化式が出来る


  111. [2010b095]*現象の｢対称性｣・余事象の使い方


  112. [2010b096]余事象の使い方


  113. [2010b097]**数直線上の移動を「最短経路」の問題にすりかえる


  114. [2010b100]*数直線上の移動を「最短経路」の問題にすりかえる


  115. [2010b102]偶数でも奇数でも結局同じ式になる


  116. [2010b103]引かれるくじの立場で考える（期待値の和と和の期待値）


  117. [2010b104]1次不定方程式の整数解


  118. [2010b105]確率がkの1次式である場合の期待値


  119. [2010b106]*xy平面上の移動をカードを並べる問題にすりかえる


  120. [2010b107]二項定理を用いた期待値計算


  121. [2010r091]数列の増減は、「階差数列」が教えてくれる


  122. [2010r092]小さな自然数から、類推によって「一般化」する


  123. [2010r093]「先攻」が有利なのか？


  124. [2010r095]相互に独立な試行を多数回反復する


  125. [2010r098]連立漸化式・合計は必ず1だ


  126. [2010r102]引かれるくじの立場で考える（期待値の和と和の期待値）


  127. [2010r104]勝負が決まったらあとのゲームはしなくてよい、でも、してもよい


  128. [2010r107]競技の途中で競技者の確率論的判断が関与する場合


  129. [2011b075]立方体の各辺の中点でできる多角形


  130. [2011b096]連立漸化式


  131. [2011b097]連立漸化式


  132. [2012b085]区別がつかないものを数えるには、まず区別がつくと考える


  133. [2012b087]同じものを含む順列・最短経路問題へのすり替え


  134. [2012b091]数列の増減は、「階差数列」が教えてくれる


  135. [2012b092]*｢重複組み合わせ｣という考え方


  136. [2012b093]**「累積確率(・・・以下である確率)」という考え方


  137. [2012b098]数列の増減は、「階差数列」が教えてくれる


  138. [2012r088]確率がkの2次関数となる


  139. [2012r093]競技者に｢優劣｣が設定されていると、長期的には劣位者が不利になる


  140. [2012r097]パスカルの三角形の対称性


  141. [2012r100]*「累積確率(・・・以下である確率)」という考え方


  142. [2012r104]nからn+1への変化を見る・初項のみが異なる漸化式


    二項定理・パスカルの三角形

  143. [2006b084]パスカルの三角形


  144. [2006b086]二項定理・剰余の問題


  145. [2006r088]*パスカルの三角形・二項定理の利用


  146. [2008b085]二項定理・剰余の問題


  147. [2008r086]**二項定理は恒等式だから、a,bに何を代入してもよい


  148. [2009r084]*二項定理を用いた不等式の証明


  149. [2010b086]二項定理・変数変換の技法


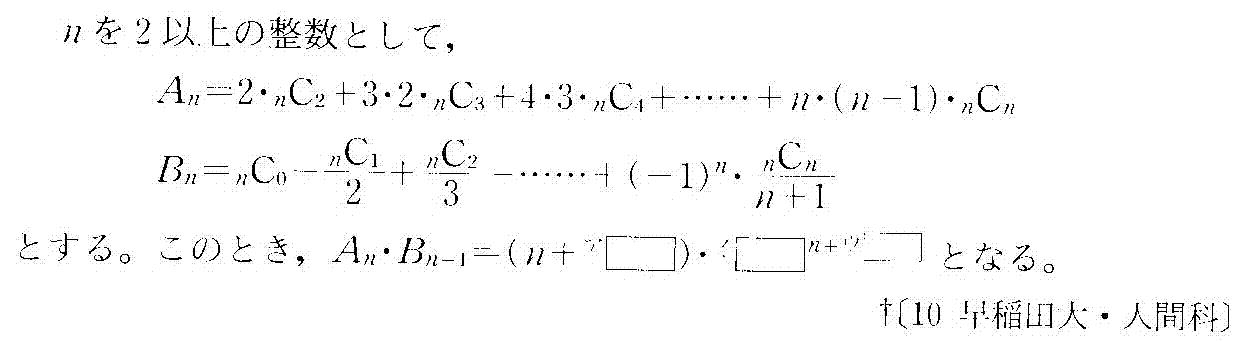
  150. [2010r085]*二項定理・剰余の問題


  151. [2011b083]二項定理・変数変換の技法


  152. [2012r083]二項定理・変数変換の技法・(1+x)nの微分


  153. [2012r084]二項定理・剰余の問題


  154. [2012r085]二項定理・剰余の問題