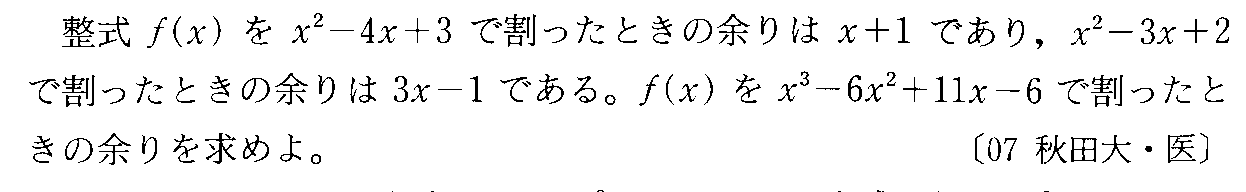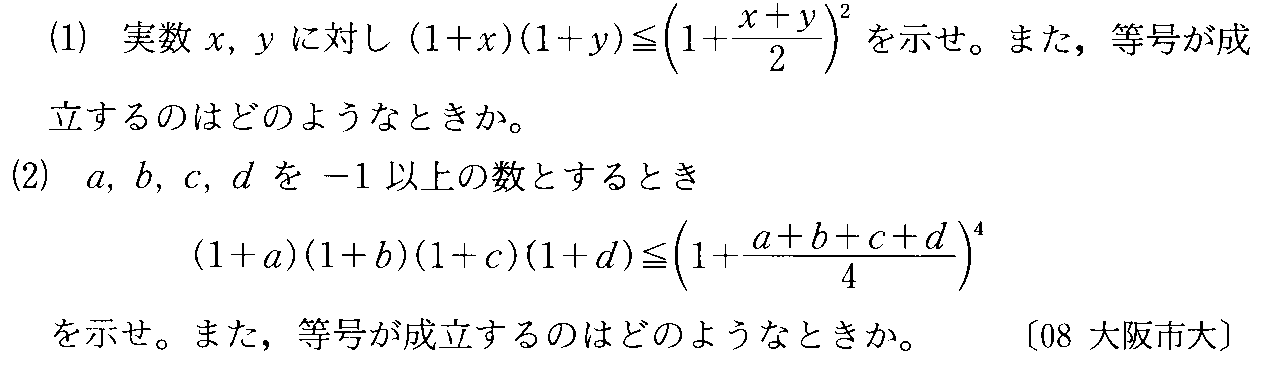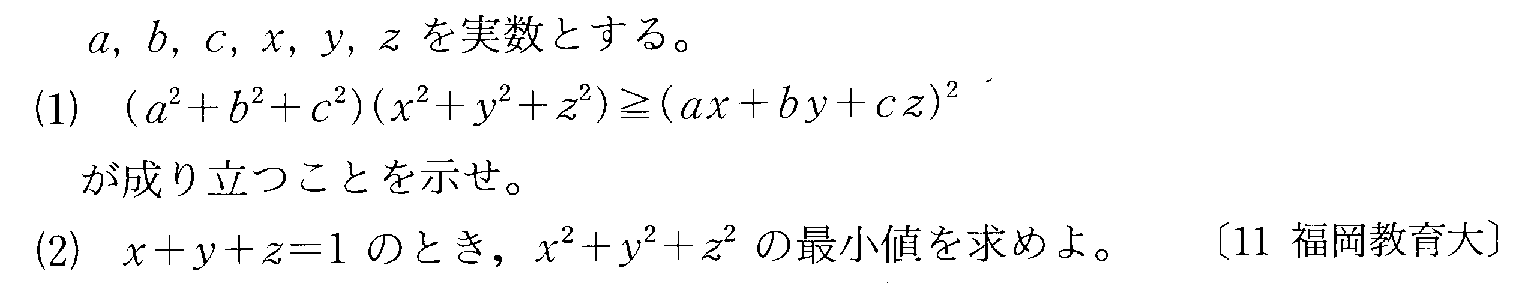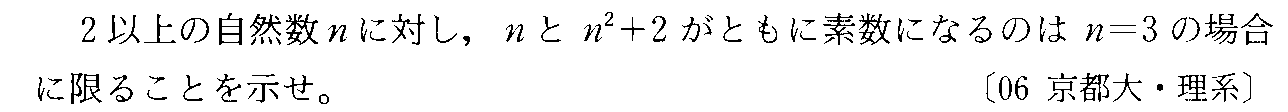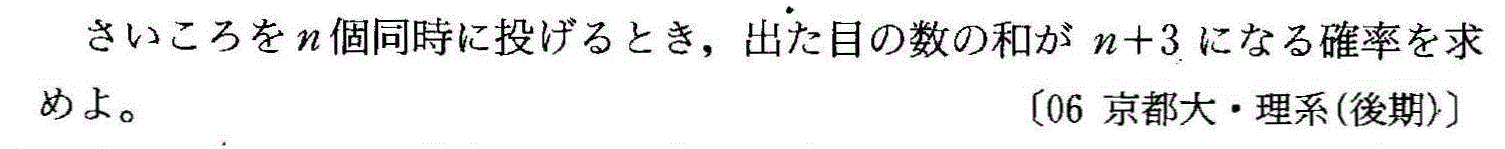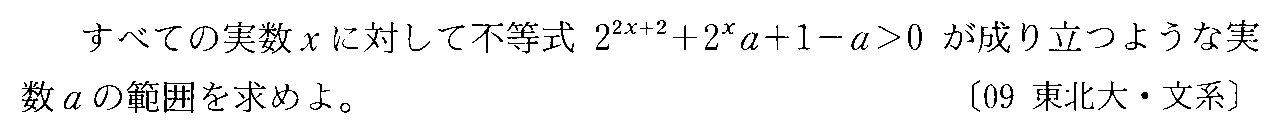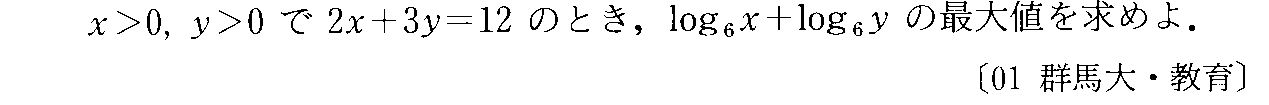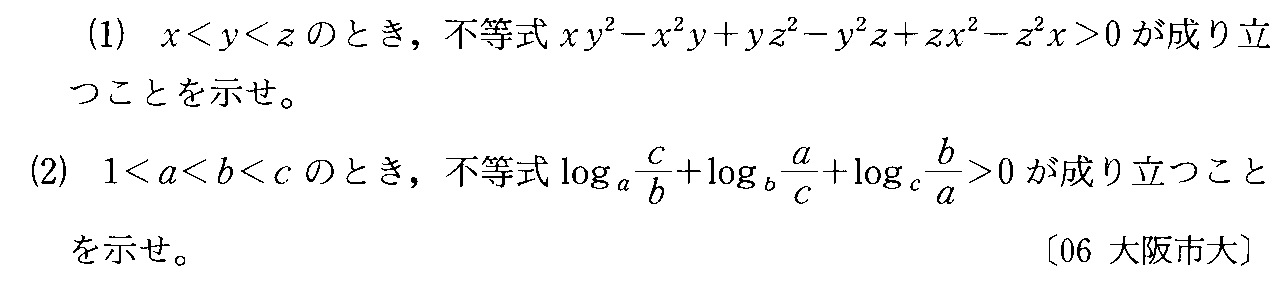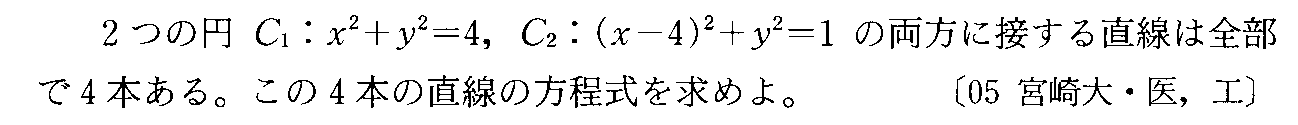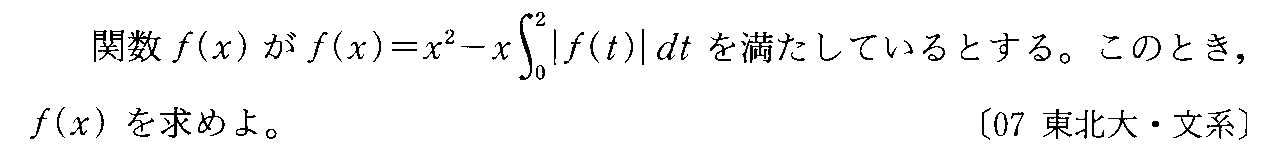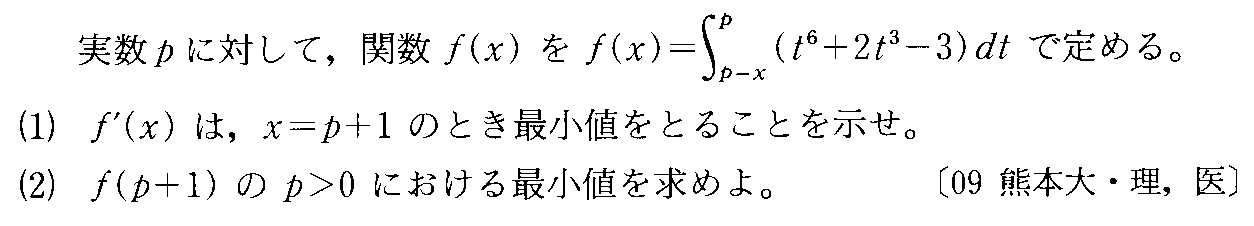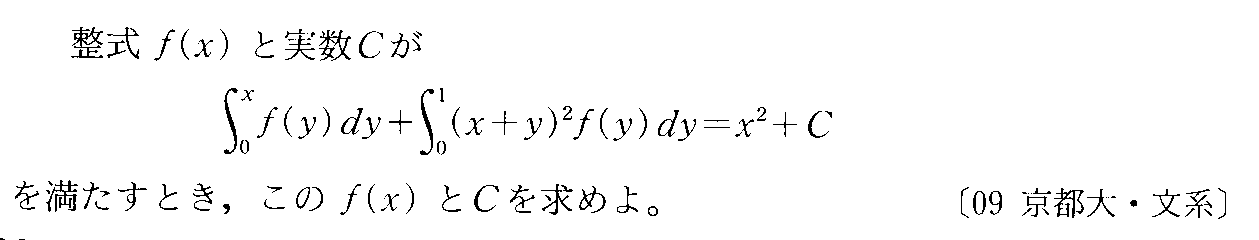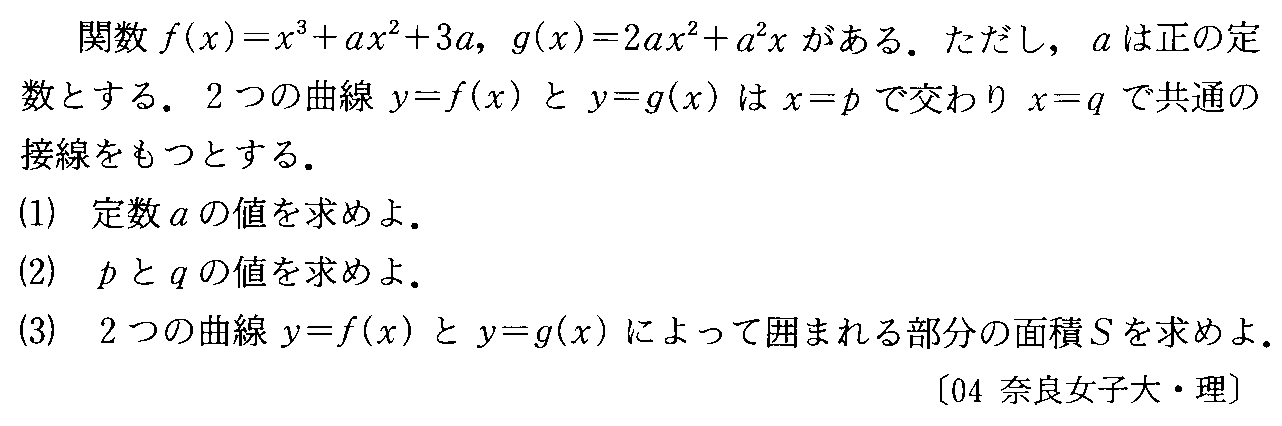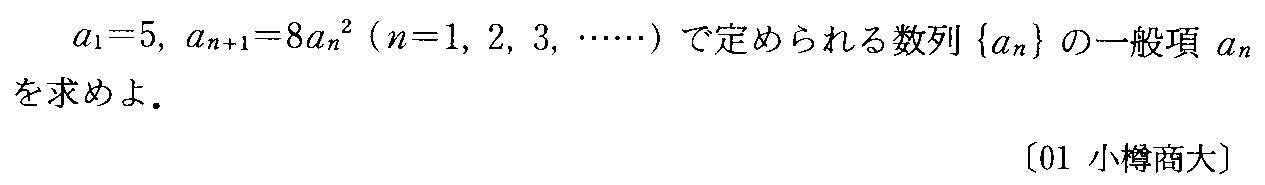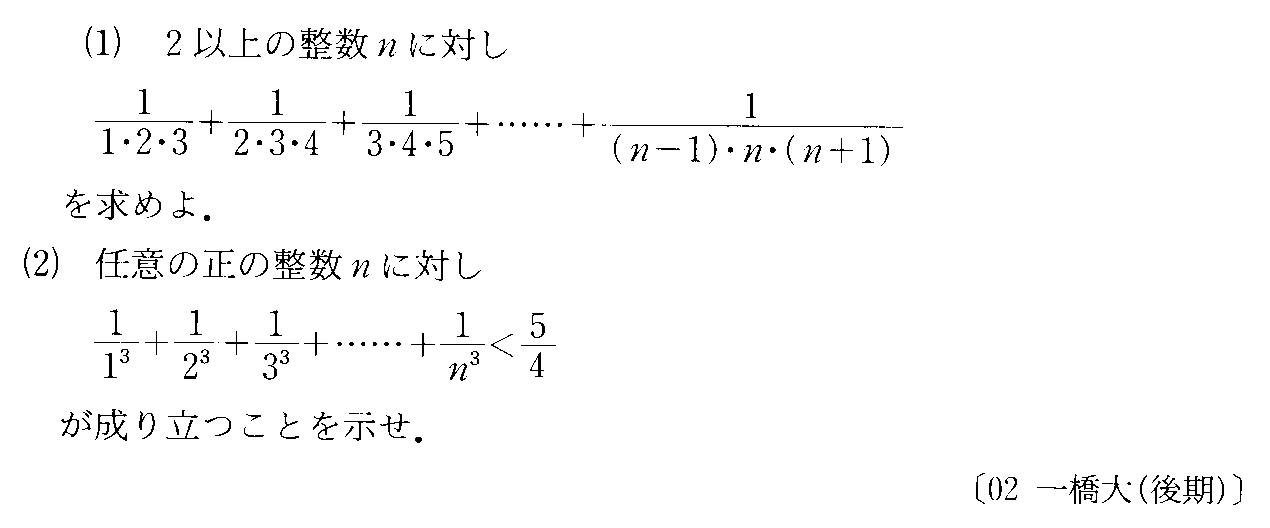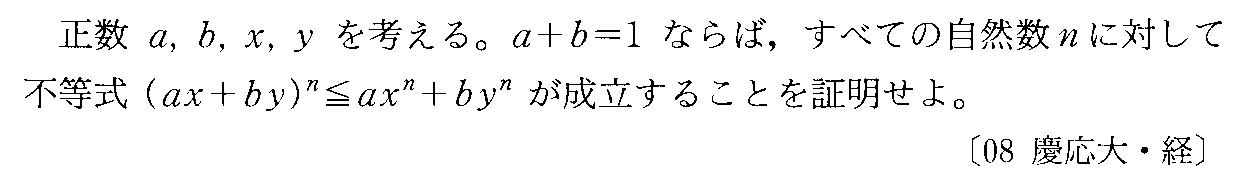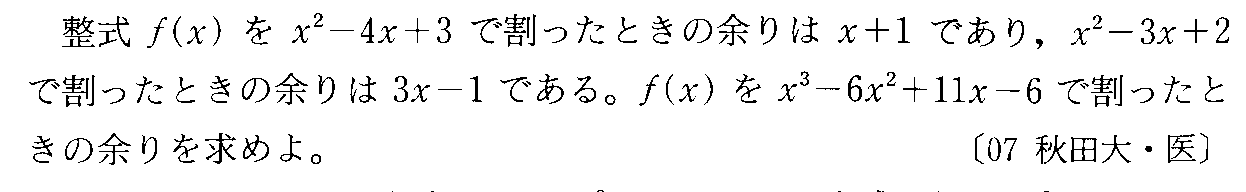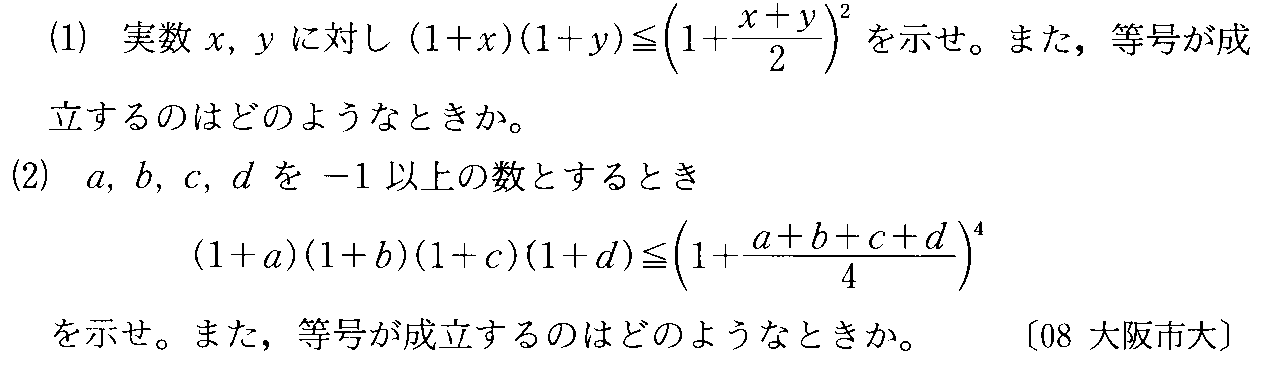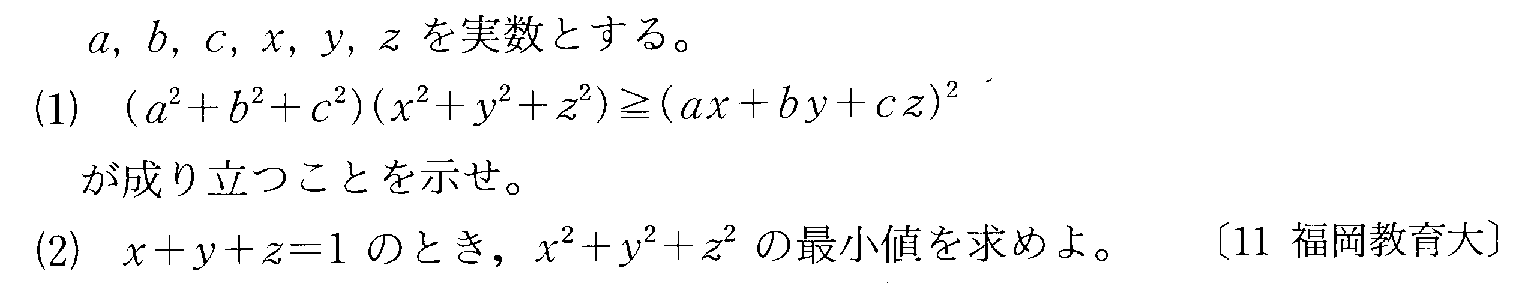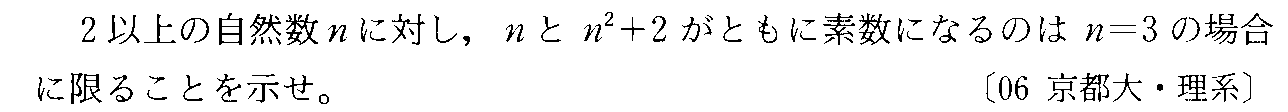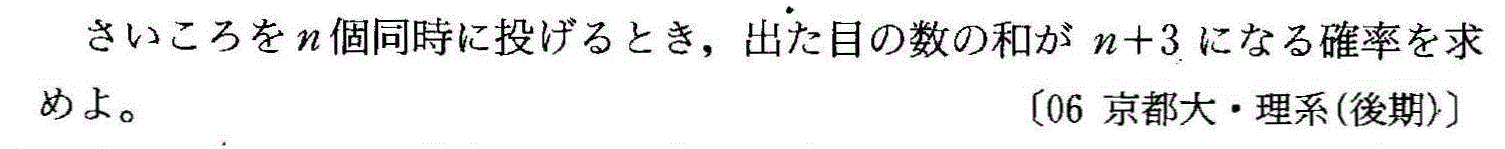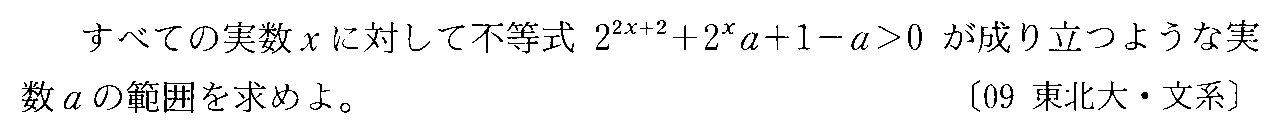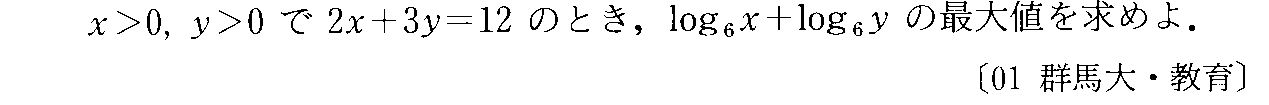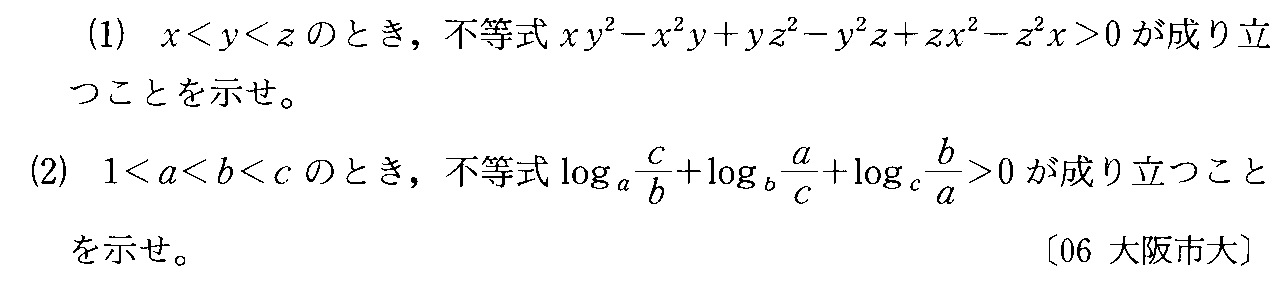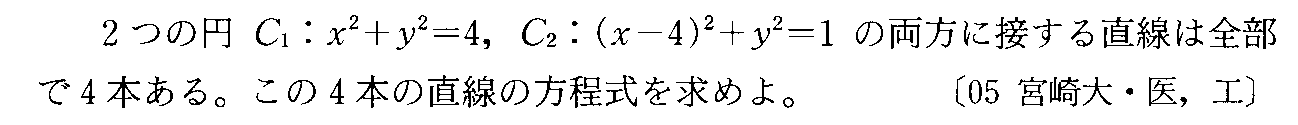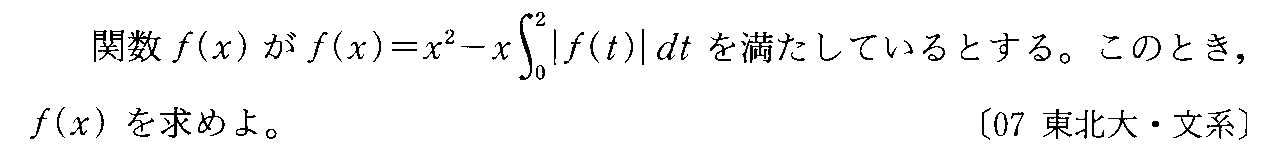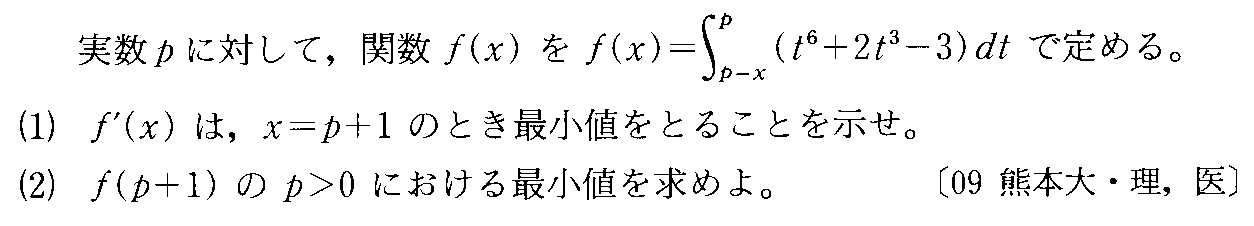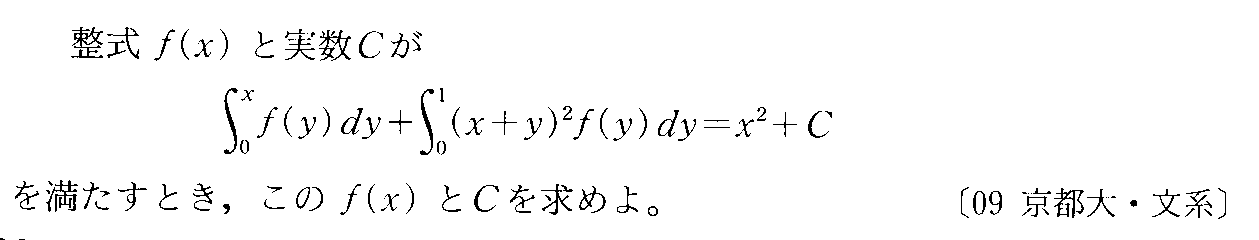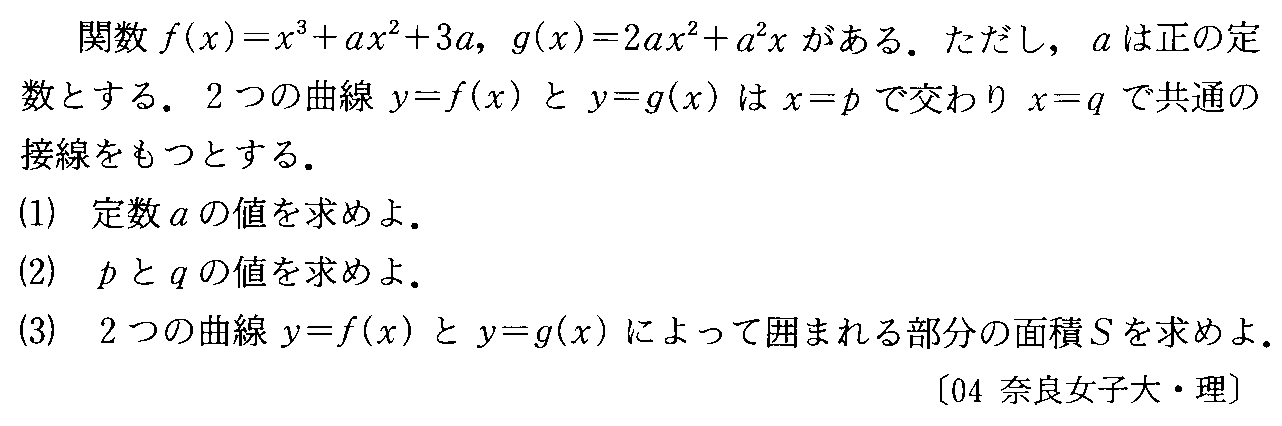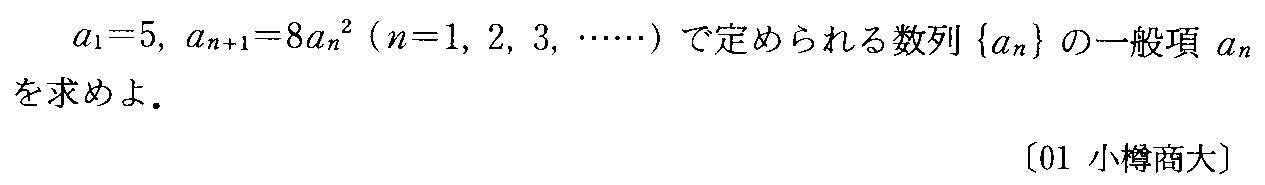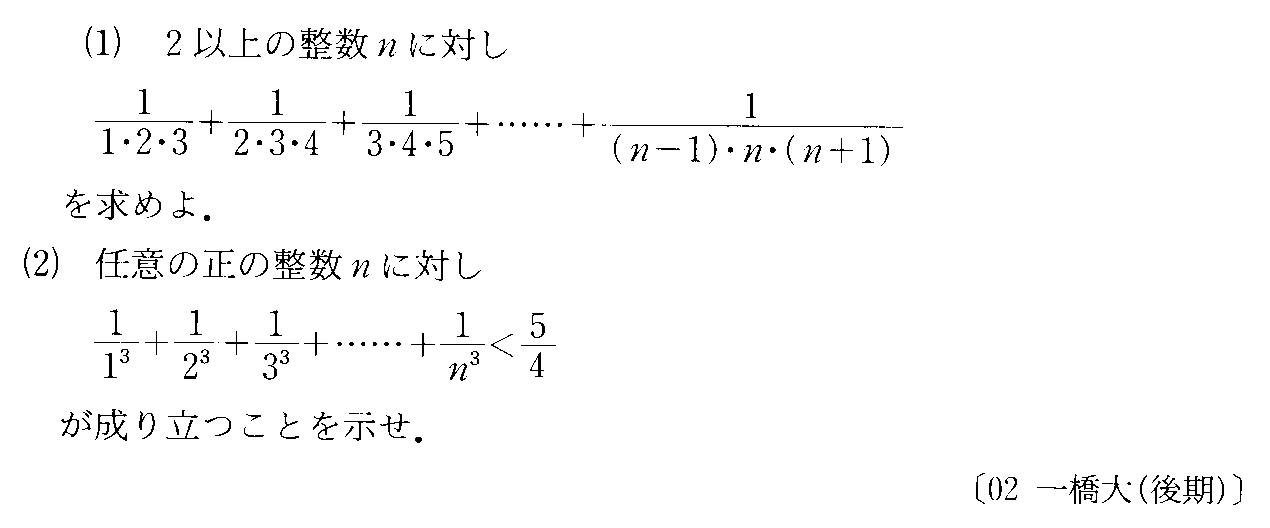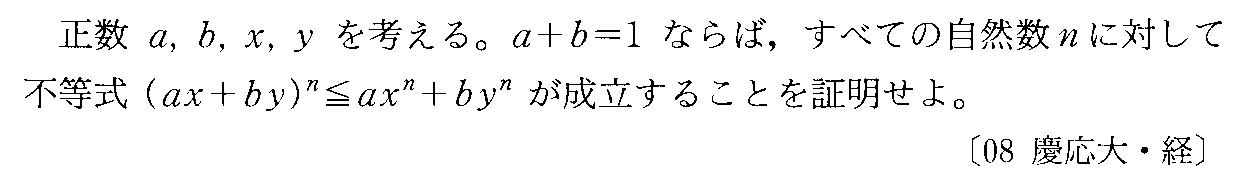命題と論証、数に関する問題
2次関数など
- 2次方程式の解の配置

- 文字係数を含む不等式

- 「あるexist」と「すべてall」

- 2次関数の最大最小・変数の変換

- 多項式の剰余
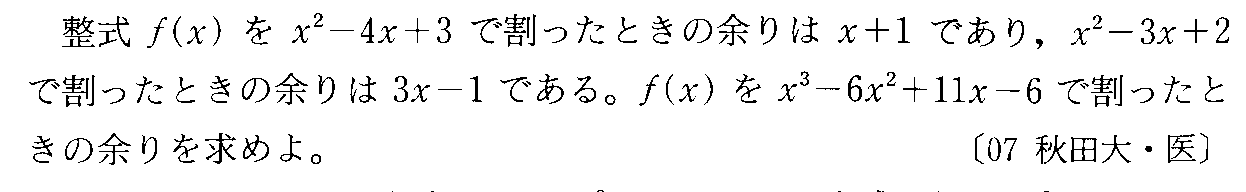
- 複素数の相等

- 不等式の証明・等号成立の条件
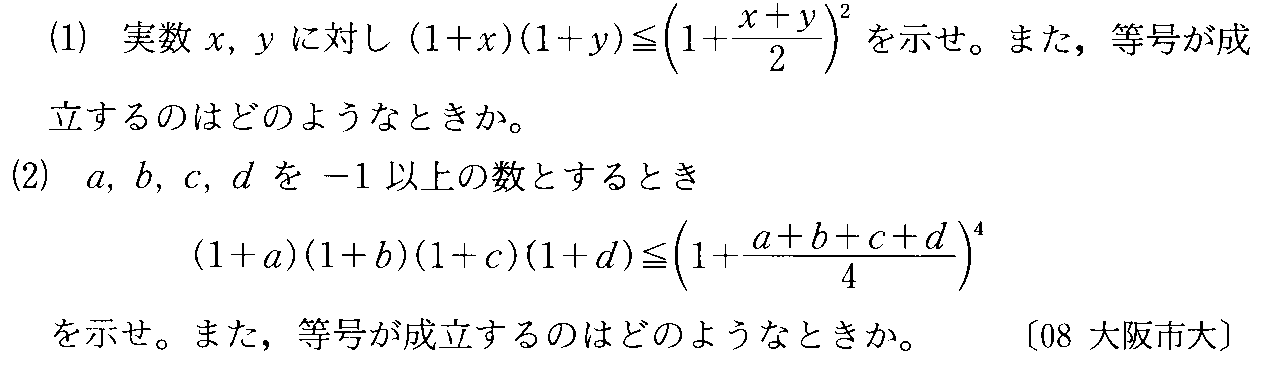
- 不等式の証明
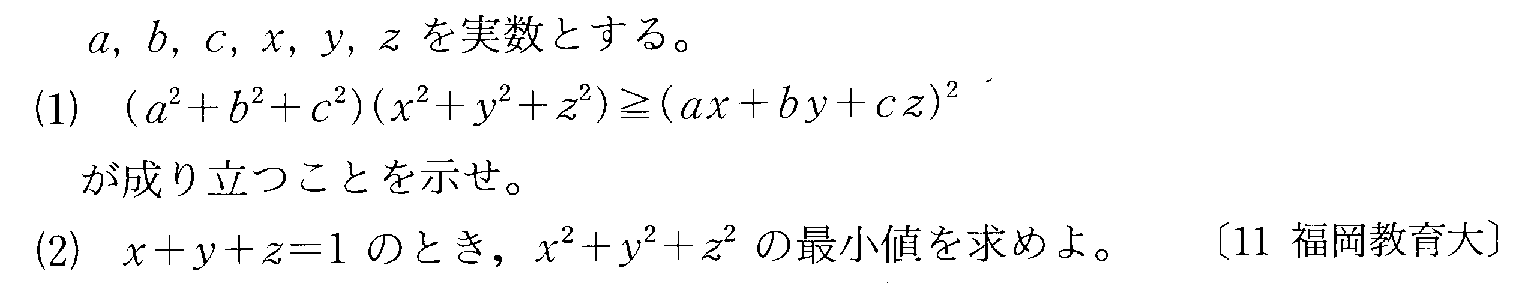
- 相加平均相乗平均

命題と論証
- 必要条件・十分条件

- 必要条件・十分条件

- 必要条件・十分条件

- 必要条件・十分条件

- 背理法

- 背理法

- 背理法

- 集合の演算

数に関する問題
- 無理数であることの証明

- 背理法・「素数」は、否定文でしか定義できない

- 排反事象の和に分ける
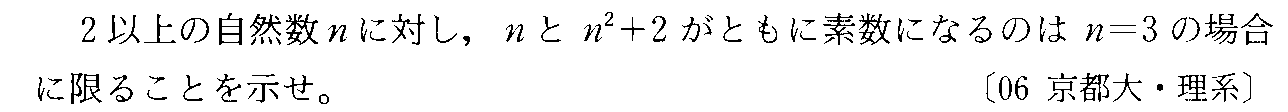
- 不定方程式の自然数解

- 不定方程式の整数解

- 不定方程式の整数解・剰余系による分類

場合の数、確率
場合の数・順列・組み合わせ
- 円順列の立体化

- 区別のつく「もの」を、区別のつかない「容器」に分ける

- 区別のつかない「もの」を、区別のつく「容器」に分ける

- 円順列の立体化

- nからn+1への変化を見る

- 「重複組み合わせ」という考え方・「一対一対応」を発見する

- 「重複組み合わせ」という考え方・パスカルの三角形

- 3次元最短経路問題・同じものを含む順列・包除原理

- 「重複組み合わせ」という考え方

集合の要素の個数
- ものを並べる話にすりかえる・自然数とは端からつけた番号である

- 二項定理の応用・n人の旅人が2部屋に泊まる

- 素数は「否定文」でしか定義できない

確率
- 勝負が決まったらあとのゲームはしなくてよい、でも、してもよい

- 数直線上の移動を「最短経路」の問題にすりかえる

- 数列の増減は、「階差数列」が教えてくれる

- 「3人から1人勝ち」と「2人から1人勝ち」では確率が異なる

- SnとPnを含む漸化式([2008r099]と同じ)

- 二項定理を用いた期待値計算

- 包除原理

- 小さな自然数から、類推によって「一般化」する

- 「重複組み合わせ」という考え方
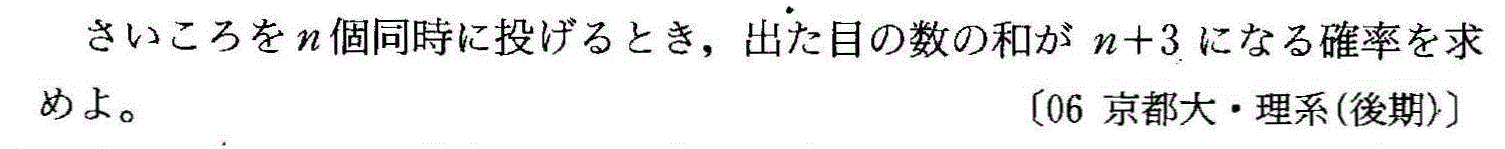
- 「同値関係」の証明・整数には偶数か奇数か、どちらかしかない

- 等確率でない試行を繰り返すと世界に偏りが生じるという話

- 四角錐だから、頂点Oだけが非対称だ

- 引かれるくじの立場で考える(期待値の和と和の期待値)

- 小さな自然数から、類推によって「一般化」する

- 「累積確率(・・・以下である確率)」という考え方([2007b088]と同じ)

- 偶数と奇数で形が異なる漸化式が出来る

- 現象の「対称性」・余事象の使い方

- 数直線上の移動を「最短経路」の問題にすりかえる

- xy平面上の移動をカードを並べる問題にすりかえる

- 「重複組み合わせ」という考え方

- 「累積確率(・・・以下である確率)」という考え方

二項定理・パスカルの三角形
- パスカルの三角形・二項定理の利用

- 二項定理を用いた不等式の証明

- 二項定理・剰余の問題

三角関数・指数関数・対数関数
三角関数
- 重心の定義・「ヘロンの公式」の証明

- 正四面体の2面のなす角

- 「和→積」が有効である場面

- 3倍角から得られる3次方程式・正五角形と「黄金比」

- 4倍角から得られる4次方程式・正多角形

- 減少である区間と増加である区間

- 置き換え、2次関数、3次関数の最大最小(←「微分・積分」)

- 三角関数の合成・置き換え、定数項に未知数を含む3次方程式の解の個数(←「微分・積分」)

指数関数・対数関数
- 置き換えをすると当然、定義域が変わる
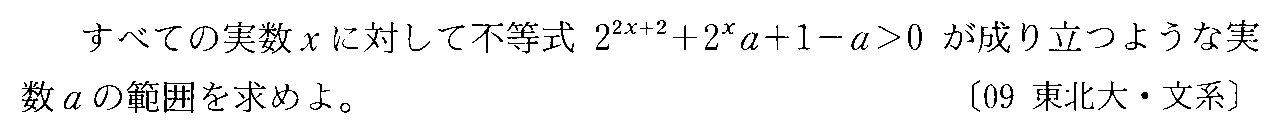
- 「相加平均と相乗平均の関係」の最大最小問題への流用
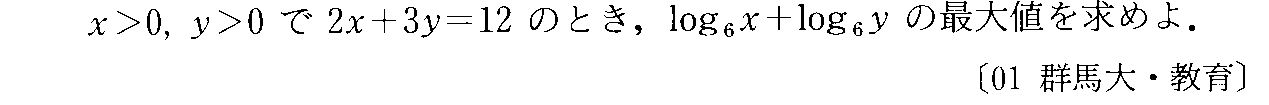
- 不等式の証明、底が1より大きいことの意味
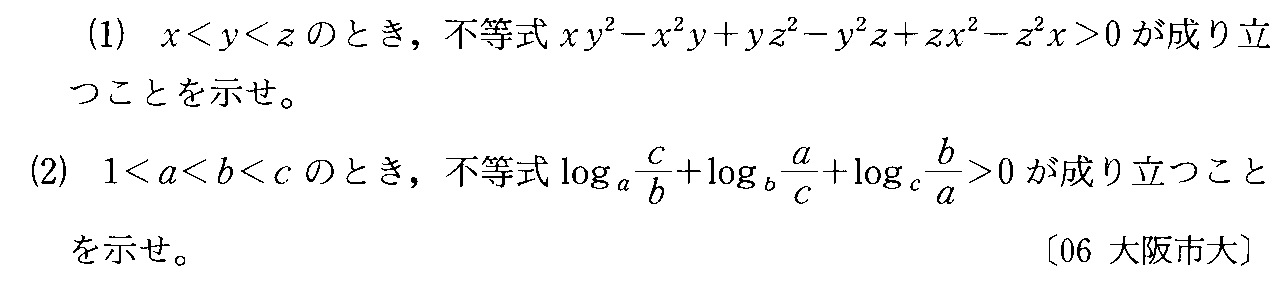
- 常用対数、桁数の問題

- 置き換え、合成関数・方程式の解の個数・相加平均と 相乗平均

- 対数関数と1次関数のグラフの交点?

- log23が無理数であることの証明・小数第1位の数字は、10倍したときの1の位の数字

図形と方程式
直線・円
- 円外の1点から引いた円の接線
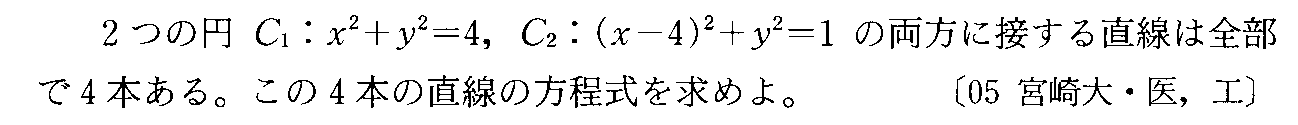
- 円と直線の位置関係・弦の長さ

軌跡・領域
- 接点を指定された場合の円の接線・2曲線の共有点を通る図形

- 恒等式の利用・直線のなす角・同じ変数を含む2曲線の交点の軌跡

- 垂心・文字のかたまりに「名前をつける」ことの効用

- 円外の1点から引いた円の接線・直線の「陰関数表示」の効用

- 軌跡(変換と逆変換が同じ?)

- 領域と最大最小・変数を自在に換えてしまうこと

微分・積分
微分
- 3次関数に曲線外の1点から引く接線の本数

- 3次関数に曲線外の1点から引く接線

- 3次関数の点対称性

- 3次関数の点対称性

- 3次関数の点対称性

- 3次関数、極大値と同じ値をとる点を求めるには?

- 最大最小

積分
- 絶対値記号を含む定積分・定積分を含む式で定義された関数
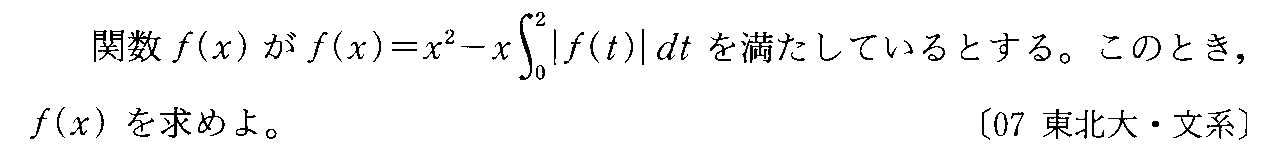
- 原始関数に名前をつける(ニュートンの公式)
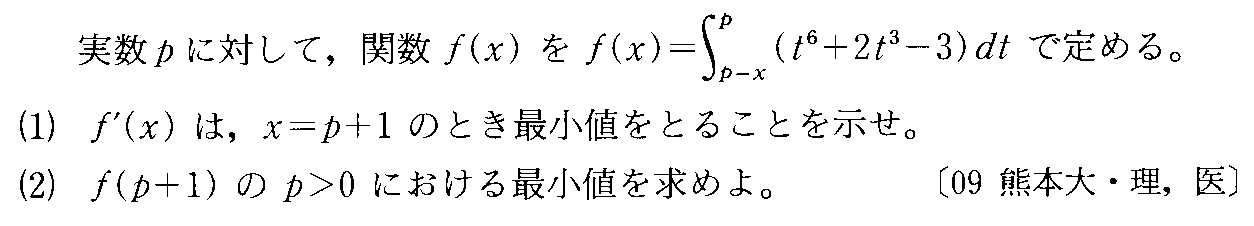
- ニュートンの公式・定積分を含む式で定義された関数
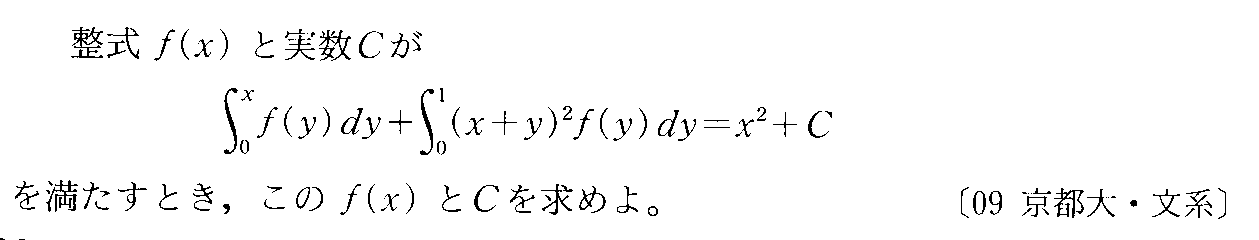
- 「6分の1」の面積公式の利用

- 放物線とその接線で囲まれた図形の面積

- 接線を共有する3次関数と2次関数で囲まれた面積
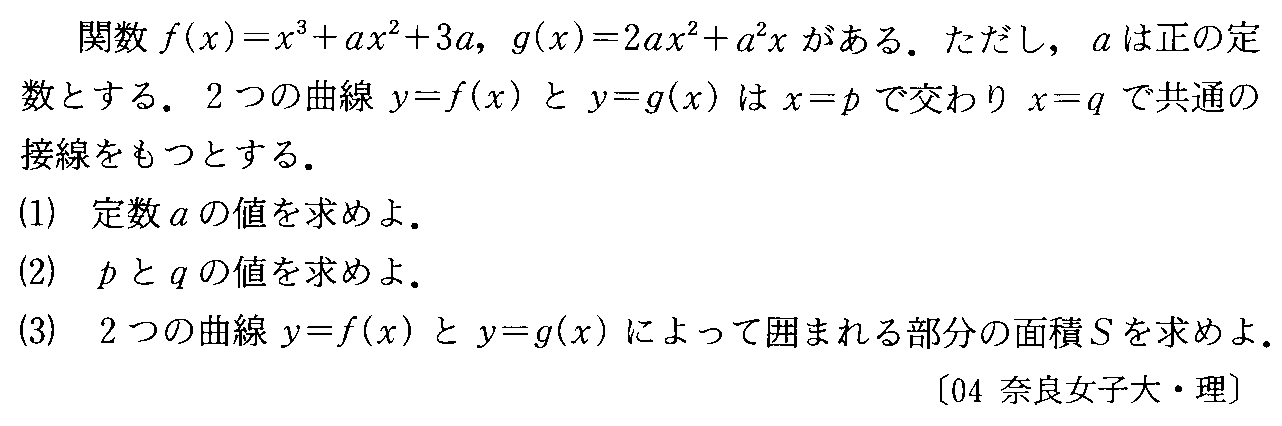
- 定数項に未知数を含む3次方程式の解の個数・曲線とその接線で囲まれた図形の面積

ベクトル
内積を用いない平面ベクトル
- 2個の1次独立ベクトルの1次結合が表す領域

内積を用いる平面ベクトル
- 始点をどこに設定するか?

- 重心、外心、垂心が同一直線上に並ぶこと

- 正五角形と黄金比

内積を用いない空間ベクトル
- 空間直線同士が交わる条件

- 直線と平面の交点

- 共面条件

- 1次独立性、始点をどこに設定するか?・2次元から3次元への拡張

- 平面直線の交点の求め方・共面条件

内積を用いる空間ベクトル
- 空間の2直線の最短距離

- 平面外の点から平面に下ろした垂線の足

数列
数列に関する様々な問題
- 「等差」×「等比」型数列の和

- 自然数の累乗の和の公式の導出

- すべての項が正の数列ならば、対数をとってもよい
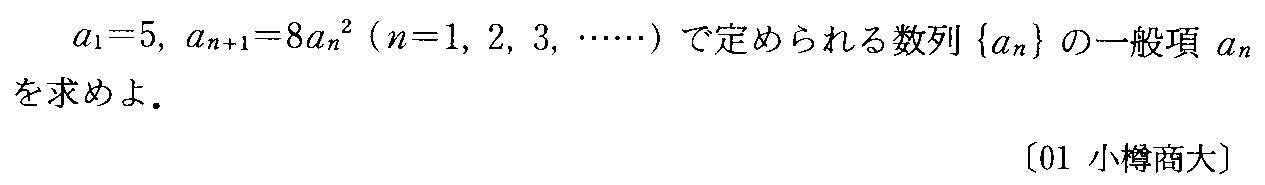
- 部分分数の差に展開する
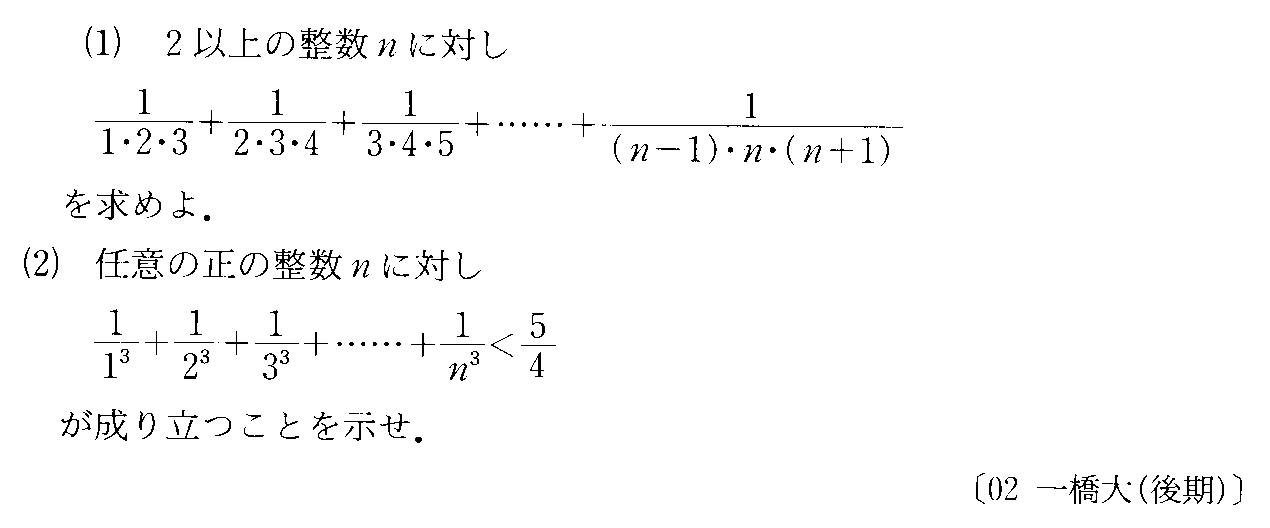
- 「余事象」の考え方

- 整数の正の約数の個数、その和

群数列
- 群数列

- 群数列として扱うことが出来る問題
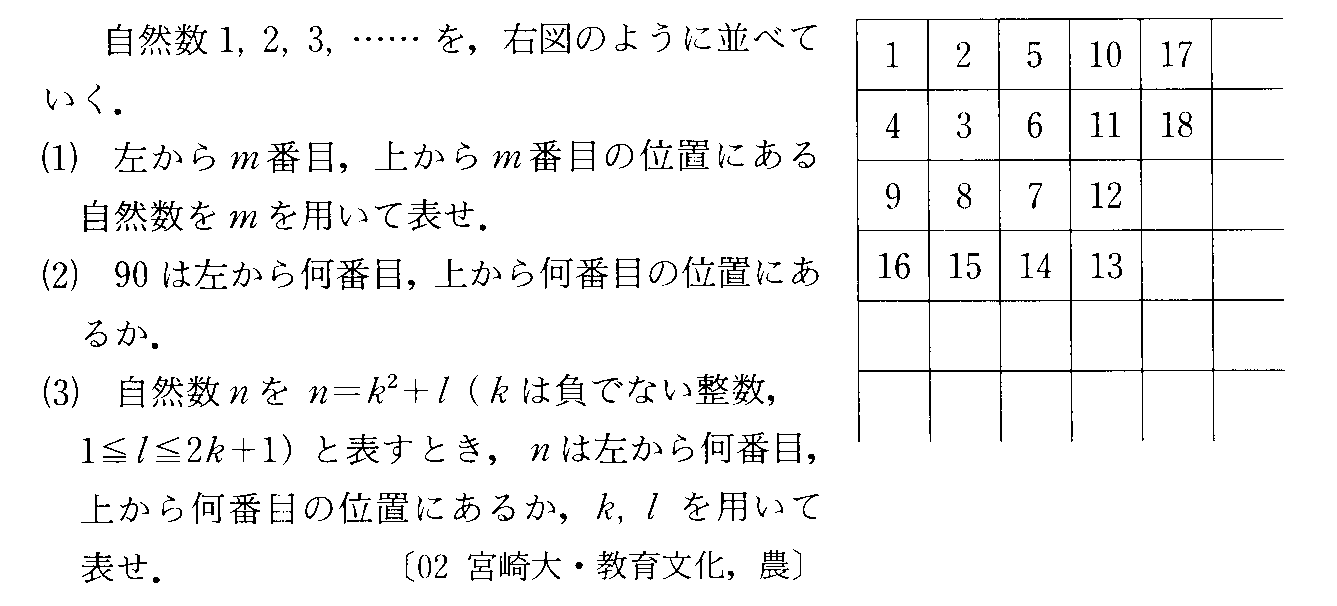
- 意外なところから群数列が現れた

漸化式
- 隣接3項間漸化式(特性方程式の解がいずれも1でない場合)・和から一般項を求める

- 隣接3項間漸化式、定数項を含む場合

- 連立漸化式・特性方程式が重解をもつ隣接3項間漸化式

- 連立漸化式

- 分数関数型漸化式

数学的帰納法
- 数学的帰納法
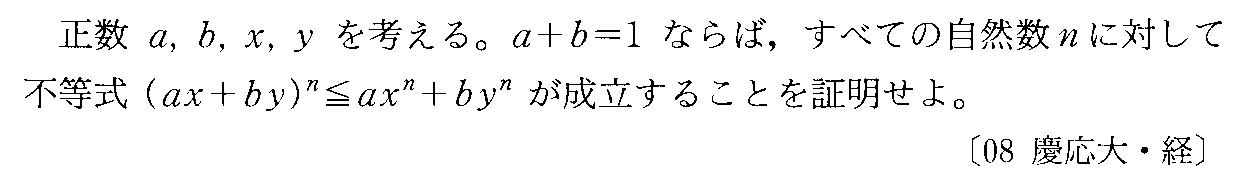
- 数学的帰納法、等号成立の条件

- 一般項の推定と帰納法による証明

格子点問題
- 格子点問題

- 3次元格子点問題