接点が与えられた場合の円の接線の公式

円C : x²+y²=r²上の点(x₁ , y₁)におけるCの接線の方程式は、
x₁x+y₁y=r² と表されることを証明せよ。
円C' : (x-x₀)²+(y-y₀)²=r²上の点(x₂ , y₂)におけるC'の接線の方程式は、
(x₂-x₀)(x-x₀)+(y₂-y₀)(y-y₀)=r²
と表されることを証明せよ。

[証明1]・・・｢法線ベクトル｣を用いて
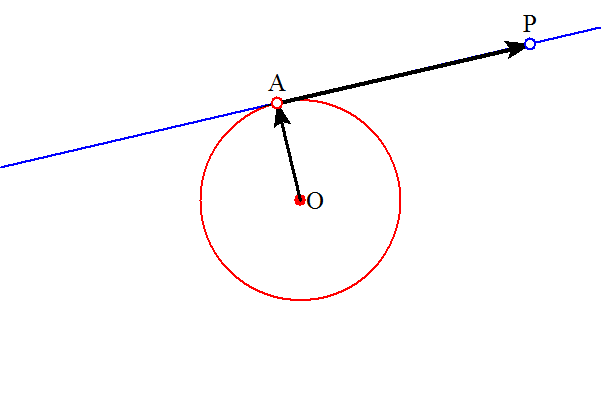
1. 求める直線は、点Aを通り、直線OAに垂直、すなわち、点Aを通り、法線ベクトルを  とする直線であるから、直線上の動点をPとすると、
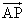    ・  =0・・・(1)
  一方、Aは、円C上の点であるから、
    ・  =r²・・・(2)
  (1)より、
    ・ ( - )=0
  すなわち、
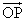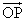    ・  -  ・ =0
  (2)を代入して、
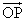    ・  = r²
  よって求める直線の方程式は、x₁x+y₁y=r²
2. B(x₀,y₀),A(x₂,y₂)として、
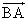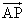    ・  =0・・・(1)
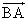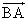    ・  =r²・・・(2)
  (1)より、
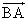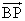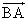    ・ ( - )=0・・・(1)
  (2)を代入して、
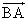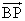    ・  = r²
  (x₂-x₀)(x-x₀)+(y₂-y₀)(y-y₀)=0
1. x₁(x-x₁)+y₁(y-y₁)=0・・・(1)
  x₁²+y₁²=r²・・・(2)
  (1)(2)より、x₁x+y₁y=r²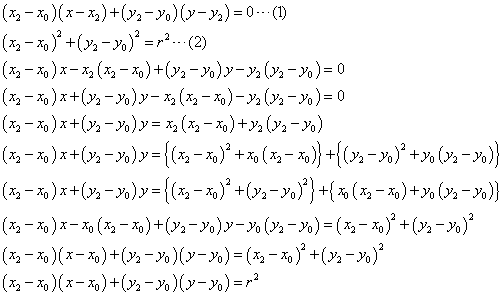
[証明2]・・・｢陰関数の微分｣(数学III)
1. x²+y²=r²の両辺をxで微分する。
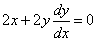
  1. y=0でないとき、
    
    したがって、点(x₁,y₁)におけるCの接線は、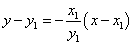
    
    これを順次変形し、(x₁,y₁)がC上の点である条件を加味すれば、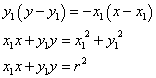
  2. y=0のとき、C上の点(-r,0),(r,0)におけるCの接線は、
    明らかに、それぞれ、x=-r,x=rである。これらは、上式を満たしている。
  よって、求める接線は、x₁x+y₁y=r²
i から ii の証明
円Cを円C'に写す変換(x軸方向にx₀、y軸方向にy₀平行移動)

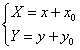
によって、(x₁ , y₁)が(x₂ , y₂)に移されたとする。すなわち、

C上の(x₁ , y₁)における接線も、C'上の(x₂ , y₂)における接線に移されるから、
x₁x+y₁y=r²  は、
(x₂-x₀)(X-x₀)+(y₂-y₀)(Y-y₀)=r²  に移される。
したがって、求める接線は、
(x₂-x₀)(x-x₀)+(y₂-y₀)(y-y₀)=r²
[例題]
- （1）上で得た「公式」によれば、
  (x₂-x₀)(x-x₀)+(y₂-y₀)(y-y₀)=r²
  に対して、(x₀ , y₀) = (4,3) , (x₂ , y₂) = (3,2) , r = √2 であるから、
  (3-4)(x-4)+(2-3)(y-3)=2
  -(x-4)-(y-3)=2
  -x+4-y+3=2
  x+y-5=0
- ところが、
  B(x₀,y₀),A(x₂,y₂)として、すなわち、
  B(4,3),A(3,2)として、
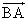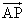    ・  =0
  (3-4)(x-3)+(2-3)(y-2)=0
  -(x-3)-(y-2)=0
  x+y-5=0
  としていけないかしら？、「公式」のほうが「速い！」かしら？
- つまり、この「公式」は、いらない、のである。
  - それがなければ解けない！
    または、
  - それ以外の方法では著しく煩雑である！
  という事情がない限り「公式」の「存在意義」は、ないのである。
  その意味で、この「公式」の適用場面を想定することは一切出来ず、したがって、「存在意義」が、ない！