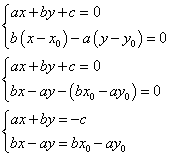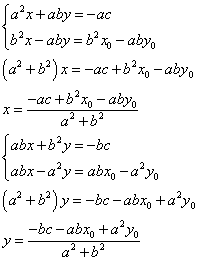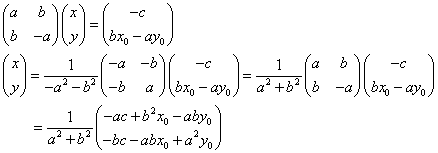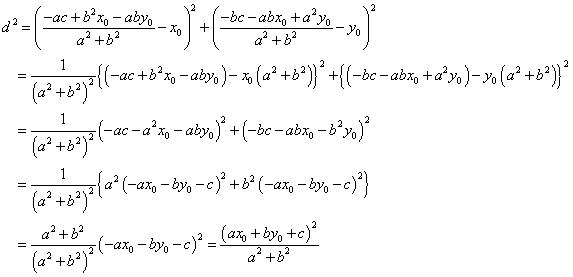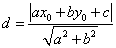直線 l : a x+b y+c = 0 に、この直線外の点 (x0 , y0) から引いた垂線の長さ d は、次の式で表されることを示せ。
- [証明1]・・・「ベクトル」を用いて(「垂線の足」Hの座標を決して求めることなく!)
- 準備
- 直線を決定するには、(i) 通過する一点と、(ii) 方向を定めることで十分である。
直線 l を、(i) 点B (x1 , y1) を通り、(ii) 法線ベクトルの一つを  = (a , b) とする直線であるとする。すなわち、 l 上の動点P(x,y)に対して、
= (a , b) とする直線であるとする。すなわち、 l 上の動点P(x,y)に対して、
 ・
・  =0・・・(1)
=0・・・(1)
- これを成分表示することによって、 x1 , y1 , c の関係が得られる。
a(x-x1)+b(y-y1)=0・・・(1')
これが、 a x+b y+c = 0 と同一の直線を表していることから、
c = - ax1 - by1 ・・・(2)
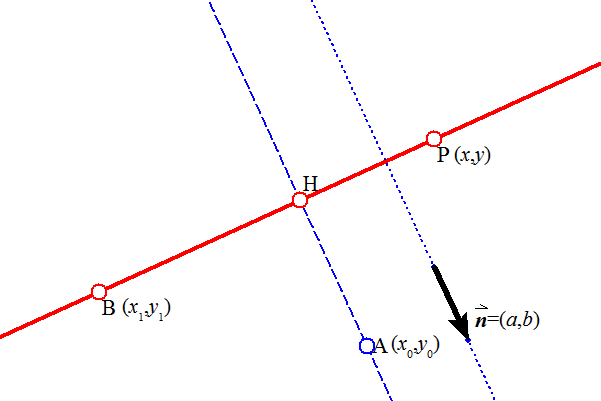
- A (x0 , y0) 、Aから直線 l に下ろした垂線の足をHとすると、求める長さ d は、
d = | 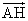 |
|
である。
- まず、Hは l 上の点であるから、(1)をみたす。すなわち、
 ・
・ 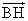 =0
=0
これをAを始点に書き直すと、
 ・ (
・ (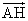 -
-  ) =0
) =0
すなわち、
 ・
・ 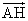 =
=  ・
・  ・・・(3)
・・・(3)
- 一方、直線AHは直線 l と垂直であるから、
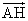 = k
= k  ・・・(4)
・・・(4)
を満たす定数 k が存在する。
(Aと直線 l との位置関係によって、 k は正の値も負の値もとりうることに注意を要する!)
- (3)(4)から、
k  ・
・  =
=  ・
・ 
すなわち、
k |  |2 =
|2 =  ・
・  ・・・(3')
・・・(3')
- また(4)から、求める長さ d は、
d = | 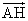 | =| k | |
| =| k | |  | ・・・(4')
| ・・・(4')
(右辺の2つの「絶対値記号」の意味の違いに注意。 | k | は、定数 k が正負いずれの値もとりうることから必要となった「絶対値」、 |  | は法線ベクトル
| は法線ベクトル  の「大きさ」である。)
の「大きさ」である。)
- したがって、(3')(4')から、
d = | 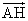 | =| k | | | =| k | |  | = | = | |  ・ ・  | | | ・・・(5) |
 |
|  | | |
(内積  ・
・  は、2つのベクトルのなす角が鋭角か鈍角であるかによって、正の値も負の値もとりうることから、「絶対値」を取る必要があるのである。)
は、2つのベクトルのなす角が鋭角か鈍角であるかによって、正の値も負の値もとりうることから、「絶対値」を取る必要があるのである。)
- こうして、すべての準備が整った。
- まず、
 ・
・  = a (x1-x0) + b (y1-y0)
= a (x1-x0) + b (y1-y0)
(2)を用いて、
 ・
・  = a (x1-x0) + b (y1-y0) = - ax0 - by0 -c
= a (x1-x0) + b (y1-y0) = - ax0 - by0 -c
したがって、
|  ・
・  | = | a (x1-x0) + b (y1-y0) | = | - ax0 - by0 -c | = | ax0 + by0 +c |
| = | a (x1-x0) + b (y1-y0) | = | - ax0 - by0 -c | = | ax0 + by0 +c |
- 一方、
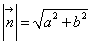
- よって、
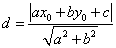
が得られた。
- 補足: | ax0 + by0 +c | の、「絶対値記号」の意味・・・「直線の『正領域』、『負領域』」
一般に、直線 l : a x+b y+c = 0 に対して、点 (X , Y) が、
- l 上の点であるとき、 a X+b Y+c = 0 である。
- l 上の点でないときは、
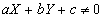 すなわち、
すなわち、
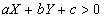 または
または 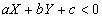 のいずれかである。
のいずれかである。
-
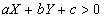 となる点 (X , Y) の集合を、直線 l の「正領域」、
となる点 (X , Y) の集合を、直線 l の「正領域」、
-
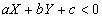 となる点 (X , Y) の集合を、直線 l の「負領域」、
となる点 (X , Y) の集合を、直線 l の「負領域」、
と呼ぶ。
- 例えば、直線 l : 2x+3y-6 = 0 に対して、
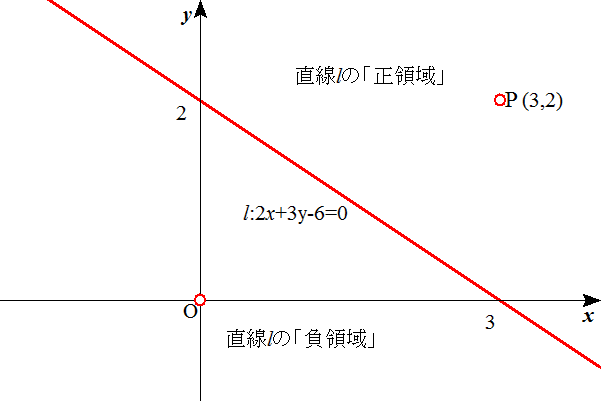
- (0,0)は、2・0+3・0-6=-6であるから、「負領域」である。(0,0)と同じ側、すなわち l の「下側」は、「負領域」である。
- (3,2)は、2・3+3・2-6=6であるから、「正領域」である。(3,2)と同じ側、すなわち l の「上側」は、「正領域」である。
- [注意]上の例で、直線 l の式を、: -2x-3y+6 = 0 と書くことも可能である。このとき「正領域」と「負領域」は逆転する。
「陰関数表示」の直線は表現方法が無数にあり、直線のどちら側が「正領域」、「負領域」であるかは、その表現方法に依存する!
- [証明2]・・・xy座標の方程式を用いて(「垂線の足」Hの座標を求めて!)
- 直線 l : a x+b y+c = 0 に対して、これと直交し、点A (x0 , y0) を通る直線 m は、
直線 m : b (x-x0)-a (y-y0) = 0
と書くことが出来る。これら2直線の交点が、Hであるから、
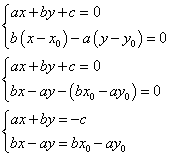
この連立方程式を解いて、
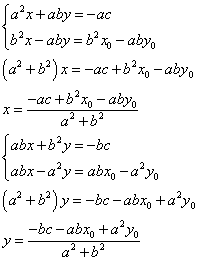
これがHの座標である。
- 行列(数学C)を用いれば、
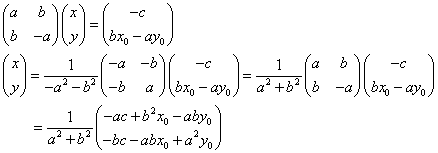
- したがって、AHの長さ d は、
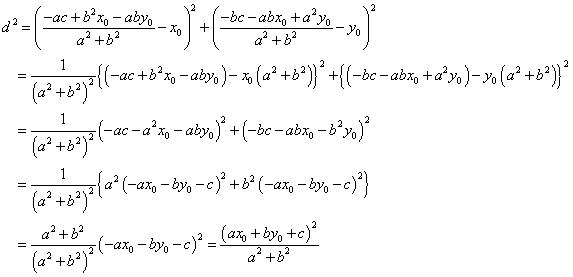
- こうして、
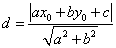
が得られた。
 = (a , b) とする直線であるとする。すなわち、 l 上の動点P(x,y)に対して、
= (a , b) とする直線であるとする。すなわち、 l 上の動点P(x,y)に対して、
 ・
・ 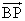 =0・・・(1)
=0・・・(1)

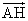 |
|
 ・
・ 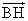 =0
=0
 ・ (
・ (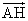 -
-  ) =0
) =0
 ・
・ 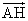 =
=  ・
・  ・・・(3)
・・・(3)
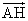 = k
= k  ・・・(4)
・・・(4)
 ・
・  =
=  ・
・ 
 |2 =
|2 =  ・
・  ・・・(3')
・・・(3')
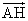 | =| k | |
| =| k | |  | ・・・(4')
| ・・・(4')
 | は法線ベクトル
| は法線ベクトル  の「大きさ」である。)
の「大きさ」である。)
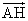 | =| k | |
| =| k | |  | =
| =  ・
・  |
|
 |
|  ・
・  は、2つのベクトルのなす角が鋭角か鈍角であるかによって、正の値も負の値もとりうることから、「絶対値」を取る必要があるのである。)
は、2つのベクトルのなす角が鋭角か鈍角であるかによって、正の値も負の値もとりうることから、「絶対値」を取る必要があるのである。)
 ・
・  = a (x1-x0) + b (y1-y0)
= a (x1-x0) + b (y1-y0)
 ・
・  = a (x1-x0) + b (y1-y0) = - ax0 - by0 -c
= a (x1-x0) + b (y1-y0) = - ax0 - by0 -c
 ・
・  | = | a (x1-x0) + b (y1-y0) | = | - ax0 - by0 -c | = | ax0 + by0 +c |
| = | a (x1-x0) + b (y1-y0) | = | - ax0 - by0 -c | = | ax0 + by0 +c |
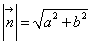
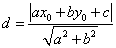
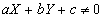 すなわち、
すなわち、
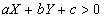 または
または 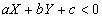 のいずれかである。
のいずれかである。
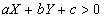 となる点 (X , Y) の集合を、直線 l の「正領域」、
となる点 (X , Y) の集合を、直線 l の「正領域」、
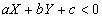 となる点 (X , Y) の集合を、直線 l の「負領域」、
となる点 (X , Y) の集合を、直線 l の「負領域」、