1. x2+y2+ax+by+c=0
    が円をあらわす必要十分条件を求めよ。
  2. 2つの円
    C1:(x-x1)2+(y-y1)2=r12
    C2:x2+y2=r22
    に対して、
    1. C1,C2が、「外接する」条件を求めよ。
    2. C1,C2が、「内接する」条件を求めよ。
    3. C1,C2が、「交わる」条件を求めよ。
  3. 2つの円
    C1:(x-x1)2+(y-y1)2=r12
    C2:x2+y2=r22
    に対して、
    C:{(x-x1)2+(y-y1)2-r12}+k(x2+y2-r22)=0
    という図形を考える。
    上のi,ii,iiiの各場合について、Cは、どのような図形をあらわすか？































  1. x2+y2+ax+by+c=0
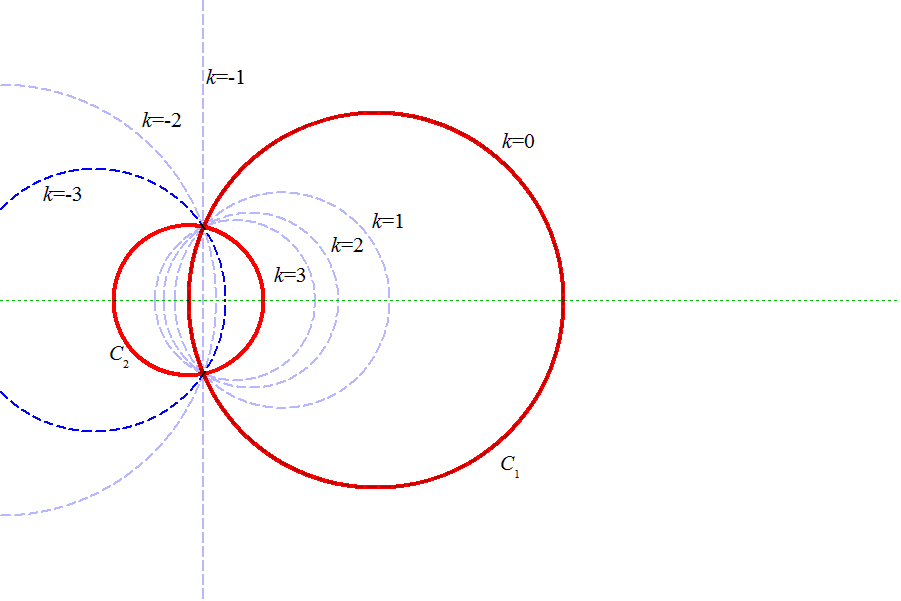
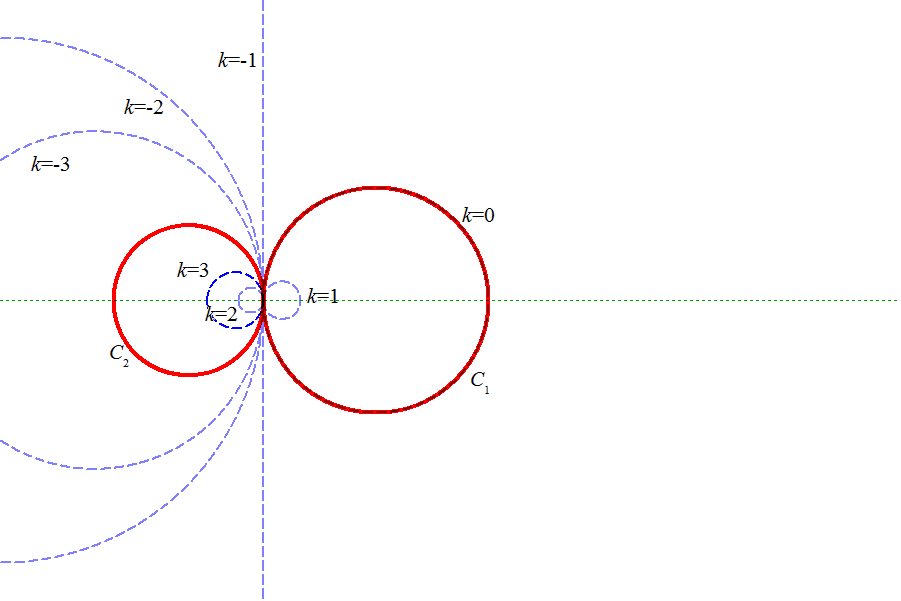
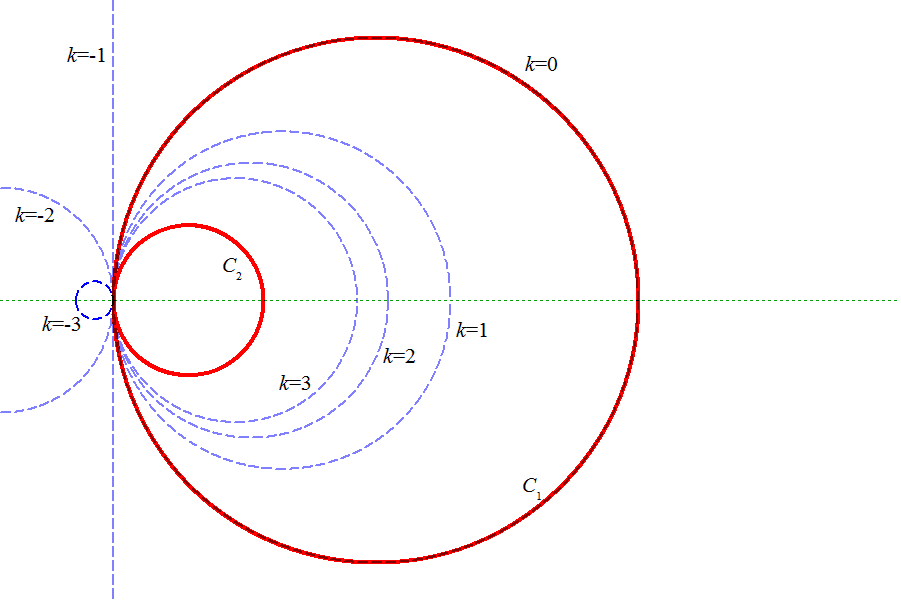
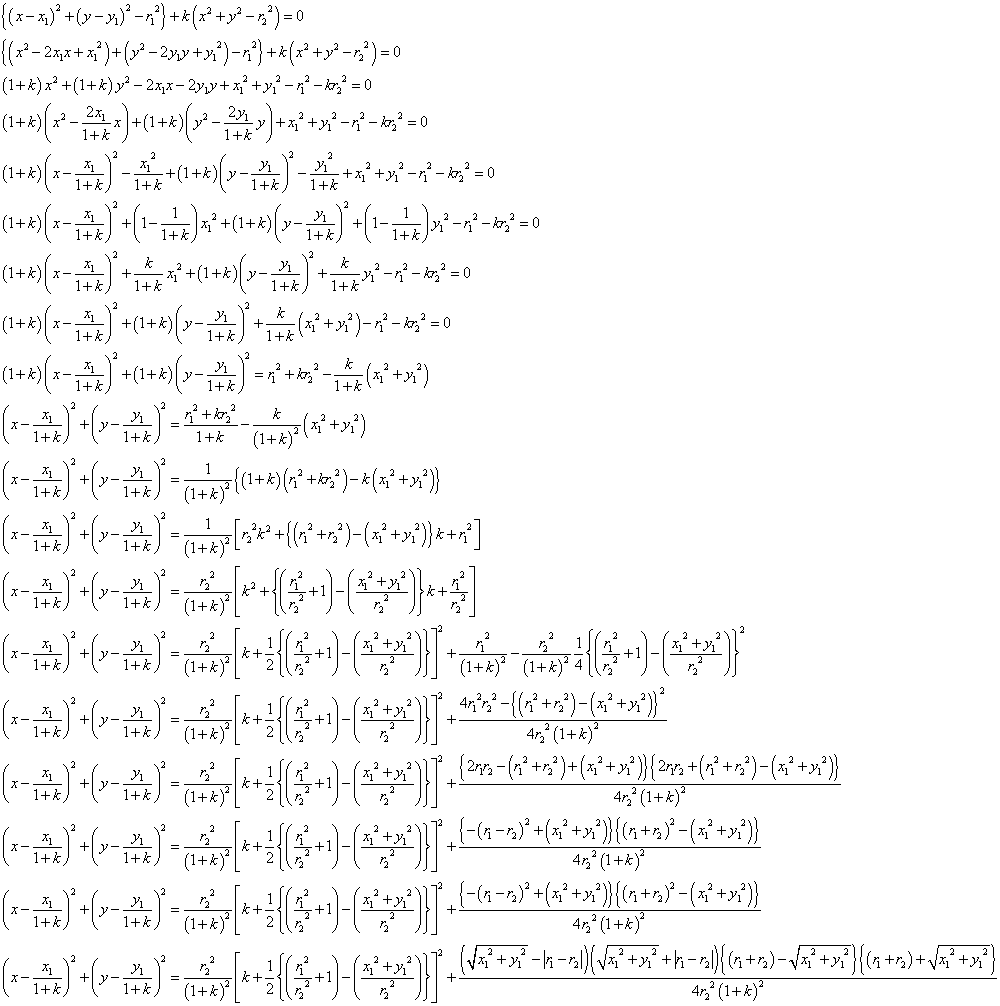    が円をあらわす必要十分条件を求めよ。
    • この式は次のように変形できるから、

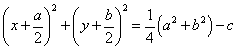
      右辺が正であれば、この式は、中心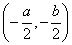、半径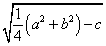の円を表す。
      すなわち、命題  A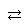B 
      • A  :  x2+y2+ax+by+c=0  が円である
      • B  :  
      において、B→Aは示された。
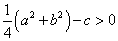
    • 次にA→Bを示したい。「対偶」を用いる。すなわち、→ を示す。
      •  :  
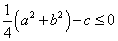
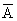      •  :  x2+y2+ax+by+c=0  が円でない

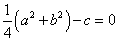      であるとき、与えられた式は、点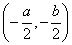を表す。
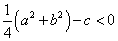      であるとき、与えられた式をみたす実数(x,y)は存在しない。
      いずれの場合も、 x2+y2+ax+by+c=0  は円ではない。よって示された。
    • 以上から、 x2+y2+ax+by+c=0  が円をあらわす必要十分条件は、
       
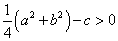
      である。





  2. 2つの円
    C1:(x-x1)2+(y-y1)2=r12
    C2:x2+y2=r22
    に対して、
    1. C1,C2が、「外接する」条件を求めよ。
    2. C1,C2が、「内接する」条件を求めよ。
    3. C1,C2が、「交わる」条件を求めよ。
    • 「三角形の成立条件」は、次のいずれかで表現される。
      • 任意の2辺の長さの和が、他の1辺の長さより大きい。
      • 任意の2辺の長さの差が、他の1辺の長さより小さい。
      • ある2辺を選んだとき、その2辺の長さの和が他の1辺の長さより大きく、かつ、その2辺の長さの差が他の1辺の長さより小さい。
    • 2つの円が「交わる」条件とは、2円の半径と、その中心を結ぶ線分が、三角形を作る条件に他ならない。
      ここでは、2円の半径を「ある2辺」として選び、中心を結ぶ線分を「他の1辺」としたわけである。
    外側で、離れている

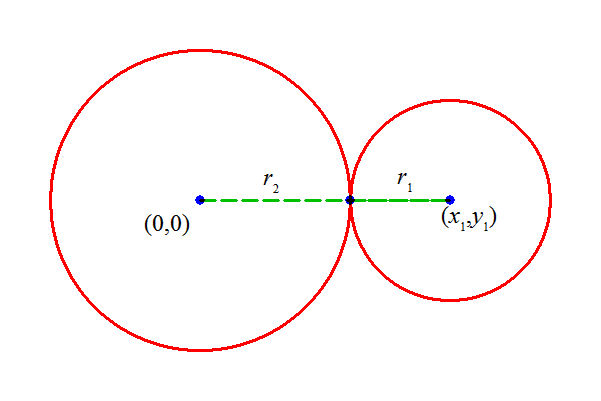    外接する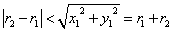

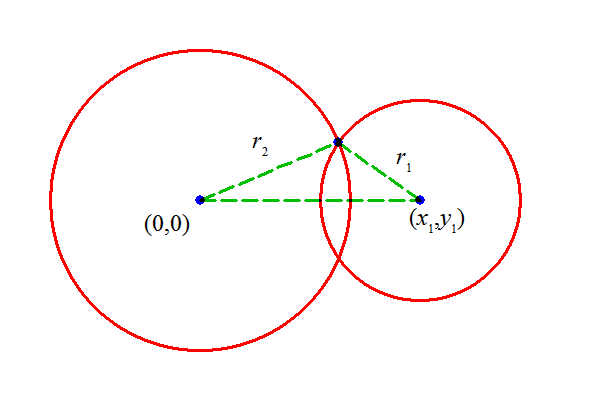    交わる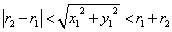

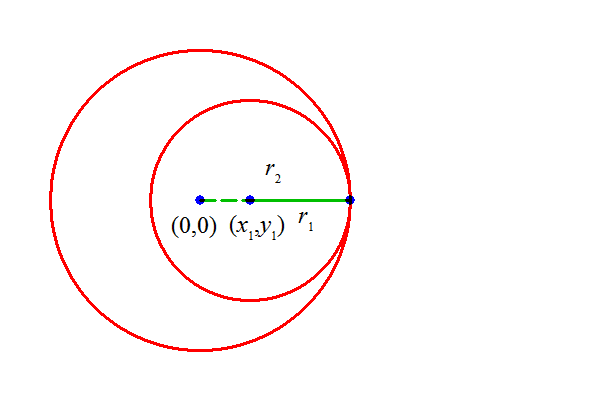    内接する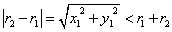

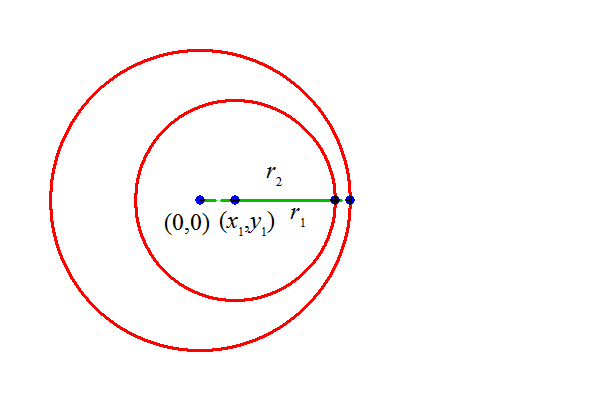    内側で、離れている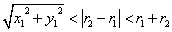



  3. 2つの円
    C1:(x-x1)2+(y-y1)2=r12
    C2:x2+y2=r22
    に対して、
    C:{(x-x1)2+(y-y1)2-r12}+k(x2+y2-r22)=0
    という図形を考える。
    上のi,ii,iiiの各場合について、Cは、どのような図形をあらわすか？