「独立 independent」は、「従属 dependent」に否定の接頭辞in-をあとからくっつけて派生した言葉だ。
「有理数」でないものが「無理数」と定義されるのと同じように、「従属」でないものが「独立」なのだ。
「他者」によって表現されてしまうことである。
- たった2個のベクトルの間の関係なら、これは「定数倍」しか考えられない。すなわち、
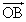 =t
=t
となる実数 t が存在するならば、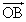 は
は の「定数倍」として表現されてしまっているから、
の「定数倍」として表現されてしまっているから、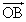 は
は に「従属」である。
に「従属」である。
t=0なら、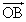 は零ベクトルだから、零ベクトルはすべてのベクトルに「従属」である。
は零ベクトルだから、零ベクトルはすべてのベクトルに「従属」である。
- 3個のベクトルの間の関係なら、あるベクトルが、他の2個のベクトルの「定数倍および足し算」で(これを「1次結合」と呼ぶ)表現されるときである。すなわち、
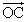 =s
=s +t
+t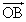
となる実数 s , t が存在するならば、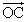 は
は と
と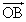 の「1次結合」として表現されてしまっているから、
の「1次結合」として表現されてしまっているから、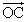 は
は と
と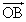 に「従属」である。
に「従属」である。
- 2個のベクトルの間の関係では、どちらの一方も、それぞれ他方の「定数倍」としては決して表現できないこと。
つまり、2次元(平面ベクトル)の世界では、
となる。- いずれも零ベクトルでなく、かつ、
- 互いに平行でないこと
ただし、本当は(!)ベクトルには「平行」という概念は、ない。ベクトルは「大きさ」と「方向」という2つの要素のみを持ち、したがって「位置」は表さない。平行移動して重なるベクトルは、「平行」なのではなくて、同じベクトルなのである。 - 3個のベクトルの間の関係では、どの1個も、他の2個の「1次結合」としては決して表現できないこと。
つまり、3次元(空間ベクトル)の世界では、
となる。- いずれも零ベクトルでなく、かつ、
- どの2個も、互いに平行でなく、かつ、
- 3個が同一平面上にないこと
こちらも、本当は(!)ベクトルは「大きさ」と「方向」という2つの要素のみを持ち、したがって「位置」は表さないから、同一平面上にあるかどうかは、本来知ったことではない(!)。3個のベクトルの根元(始点)を1点にそろえた場合に、という意味である。
|
|
- 始点のつけかえルール
もとのベクトルの「終点から始点を引く」。ベクトルは「幾何学」の道具ではない!、「線形代数学」という分野の演算システムの一つなのだ。図を描いてみて考えつく、のではなく、まったく形式的な演算で結論が得られるところに意義がある!- 始点のつけかえルール
 =
=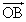 -
-
- 始点のつけかえルール
- 共線条件(3点が同一直線上にある条件)
- 異なる2点が与えられれば、それらを通る直線がただ1本、決定する。
- ここに新たな3点めが現れたとき、それがこの直線上にあるためには条件が必要だ。
ここに上の「始点のつけかえルール」を適用すると、- 共線条件
Pが直線AB上にあるならば、
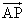 =t
=t ・・・(1)
・・・(1)
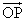 =(1-t)
=(1-t) +t
+t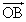 ・・・(2)
・・・(2)
もちろん、(1),(2)は同値である。
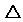 ABCにおいて、ABの中点D、ACを2:1に内分する点をE、線分CDと線分BEの交点をPとするとき、CP:PD、BP:PEを求めよ。
ABCにおいて、ABの中点D、ACを2:1に内分する点をE、線分CDと線分BEの交点をPとするとき、CP:PD、BP:PEを求めよ。
- PがCD上にあることから、
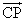 =s
=s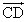
- PがBE上にあることから、
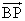 =t
=t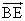
- これらを「始点のつけかえルール」など、を用いて2個の1次独立ベクトルの1次結合で表現する。
そんな方法は、ただ一通り(一意的に)しか存在しないはずだから、
2個の1次独立ベクトルの係数は、それぞれ等しい! - こうして「未知数2個」に対して「条件式2個」が得られるから、必ず、解ける。
|
|
- 始点のつけかえルール
- 共線条件(3点が同一直線上にある条件)
- 共面条件(4点が同一平面上にある条件)
- 同一直線上にない3点が与えられれば、それらを含む平面がただ1つ、決定する。
- ここに新たな4点めが現れたとき、それがこの平面上にあるためには条件が必要だ。
ここに上の「始点のつけかえルール」を適用すると、- 共面条件
Pが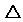 ABCを含む平面上にあるならば、
ABCを含む平面上にあるならば、
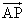 =u
=u +v
+v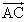 ・・・(1)
・・・(1)
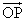 =(1-u-v)
=(1-u-v) +u
+u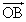 +v
+v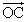 ・・・(2)
・・・(2)
もちろん、(1),(2)は同値である。
四面体ABCDにおいて、
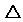 BCDの重心G、ADの中点M、線分AGと
BCDの重心G、ADの中点M、線分AGと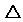 BMCを含む平面との交点をPとするとき、AP:PGを求めよ。
BMCを含む平面との交点をPとするとき、AP:PGを求めよ。
- PがAG上にあることから、
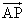 =w
=w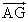
- Pが
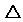 BMCを含む平面上にあることから、
BMCを含む平面上にあることから、
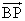 =u
=u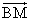 +v
+v
- これらを「始点のつけかえルール」など、を用いて3個の1次独立ベクトルの1次結合で表現する。
そんな方法は、ただ一通り(一意的に)しか存在しないはずだから、
3個の1次独立ベクトルの係数は、それぞれ等しい! - こうして「未知数3個」に対して「条件式3個」が得られるから、必ず、解ける。
- ここまでは、どんな三角形でも、どんな四面体でも、成り立つ話しかしてこなかった。
長さを問題にする場合でも、内分比のような相対的な値しか問題にしてこなかった。
- 形の特定された三角形、四面体、すなわち、角度や、絶対的な長さを問題にするには、「内積」の値、という新たな「情報」が必要になる。
これは「三角形の合同条件」に対応している。「3辺相等」、「2辺夾角相等」、「2角夾辺相等」、いずれも「情報」は3個。「合同条件」というのは、この世にそのような三角形はただ一つしかない、という意味で、三角形の形が特定される条件なのである。- 平面ベクトルでは2個の1次独立な「基底」ですべてが表現できた。
それらの内積の可能な組み合わせは、3個しかない。
・・・例えば、「基底」が、 、
、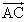 なら、
なら、
 ・
・ 、
、 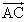 ・
・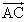 、
、  ・
・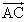
- 空間ベクトルでは3個の1次独立な「基底」ですべてが表現できた。
それらの内積の可能な組み合わせは、6個しかない。
・・・例えば、「基底」が、 、
、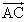 、
、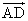 なら、
なら、
 ・
・ 、
、 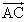 ・
・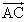 、
、 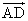 ・
・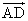
 ・
・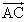 、
、 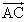 ・
・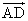 、
、 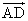 ・
・
- 平面ベクトルでは2個の1次独立な「基底」ですべてが表現できた。
- 内積を用いる空間ベクトルに固有の「道具(ツール)」
- 平面 α と直線 l が「垂直である」とは、どういうことか?
- 直線 l が、平面 α に含まれる任意の直線と「垂直である」。
- ところで、平面 α に含まれる任意の直線上の任意のベクトルは、
平面 α 上の、たった2個の1次独立ベクトルの1次結合で、
表現される!、だから、
- 直線 l が、平面 α に含まれる2個の1次独立ベクトルと「垂直」であればよい。
- 平面 α と直線 l が「垂直である」とは、どういうことか?
「外心」、「内心」、「垂心」はいずれも、三角形の形状が特定されない限り、場所を特定することが出来ない。すなわち「内積」を必要とする。
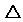 ABCにおいて、AB=AC=2、BC=3とする。重心G、外心O、内心I、垂心Hとするとき、
ABCにおいて、AB=AC=2、BC=3とする。重心G、外心O、内心I、垂心Hとするとき、
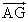 、
、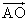 、
、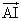 、
、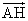 を
を 、
、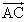 で表せ。
で表せ。
4点O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,
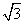 )を頂点とする四面体OABCについて、
)を頂点とする四面体OABCについて、Oから
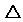 ABCを含む平面に下ろした垂線の足をHとするとき、
ABCを含む平面に下ろした垂線の足をHとするとき、
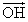 を
を 、
、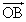 、
、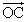 で表せ。
で表せ。
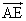 =u
=u