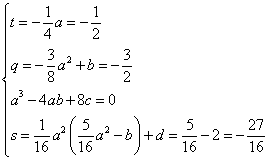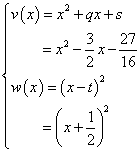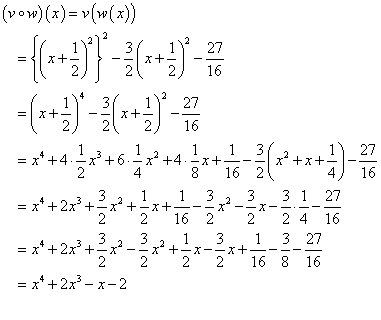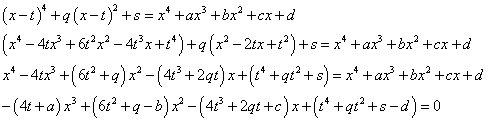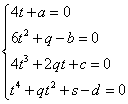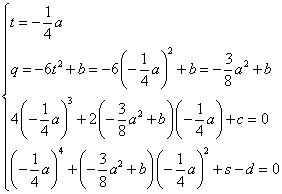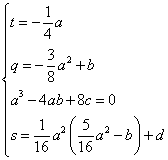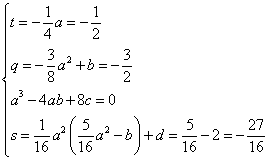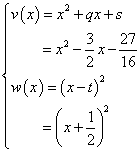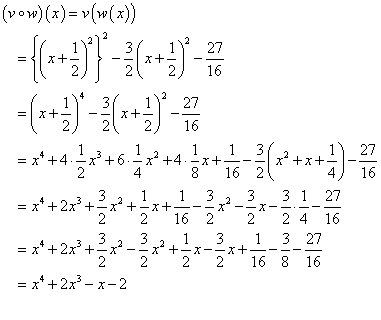4次関数  f(x)  =  x4+ax3+bx2+cx+d  が、y軸に平行な直線に関して対称であるとき、a  ,  b  ,  c  ,  d  のみたすべき関係を示せ。
また、このとき、f(x)は、二つの2次関数の合成関数としてあらわされることを示せ。
g(x)  =  x4+px3+qx2+rx+s  が、奇数次の項をもたないとき、すなわち、  p  =  r  =  0  であるとき、g(x)は「偶関数」であるから、y軸対象である。
これを、x軸方向に  t  平行移動して得られた関数が  f(x)  である、とすれば、すなわち、
g(x)  =  x4+qx2+s  に対して、  g(x-t)  =  f(x)  、すなわち、
(x-t)4+q(x-t)2+s  =  x4+ax3+bx2+cx+d  
となる  q  ,s  ,  t  が定められるならば、  f(x)  は、  y  軸に平行な直線  x  =  t  に関して対称である。

また、  g(x)  は明らかに、
  u(x)  =  x2
  v(x)  =  x2+qx+s  
に対して、  g(x)  =  (v・u)(x)  と、二つの2次関数の合成関数とかけるから、
f(x)  =  g(x-t)  =  (v・u)(x-t)  
ここに、
  w(x)  =  (x-t)2
として、
f(x)  =  (v・w)x  
まず、 g(x)  =  x4+px3+qx2+rx+s  が、奇数次の項をもたないこと、すなわち、  p  =  r  =  0  であることが、g(x)がy軸対象であることの、必要かつ十分条件であることを証明する。
次に、g(x)  =  x4+qx2+s  に対して、  g(x-t)  =  f(x)  、すなわち、
(x-t)4+q(x-t)2+s  =  x4+ax3+bx2+cx+d  
となる  q  ,s  ,  t  を定めたい。



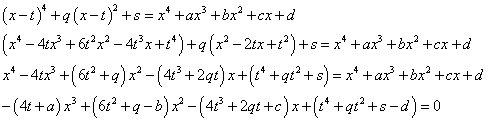
これが任意のxに対して成立するから、

    

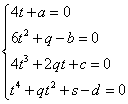
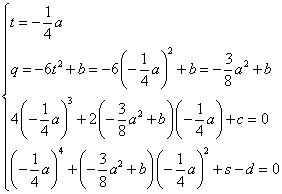
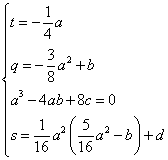
こうして、  a  ,  b  ,  c  ,  d  は、
  a3-4ab+8c  =0  
という関係をみたすべきことがわかった。ただし、  d  は任意である。

また、  q  ,s  ,  t  を、  a  ,b  ,  c  ,  d  であらわすことができた。

f(x)  =  (v・w)x  をみたすv(x)、w(x)は、

となる。
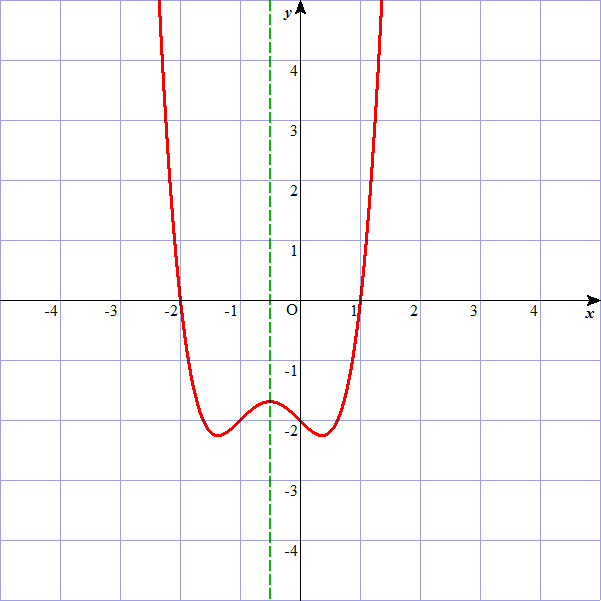
確認してみる。  a = 2  ,  b = 0  ,  c = -1  ,  d = -2  に対して、