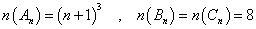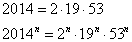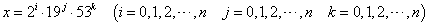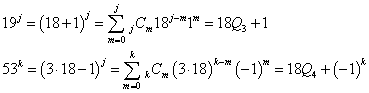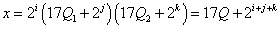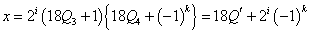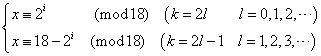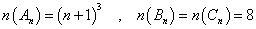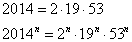
---

したがって、2014ⁿの正の約数xは次のようにかくことができる。

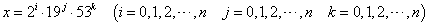
ここで、

また、

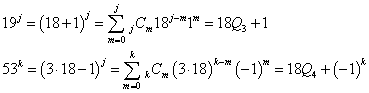
であるから、


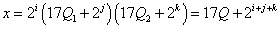
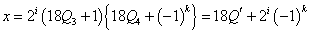
これは「合同式」を用いると、


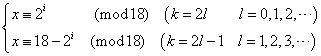
すなわち、

• xを17で割った余りは、2^i+j+kを17で割った余りと等しく、
• xを18で割った余りは、
  • kが偶数のときは、2^jを、
  • kが奇数のときは、18-2^jを、
  それぞれ18で割った余りと等しい

ことを示している。調べてみると、下の表のように、

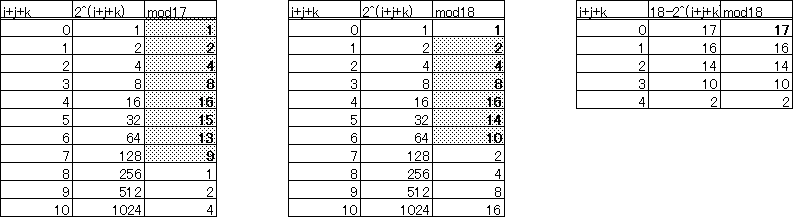
• 17で割った余りは、(1,2,4,8,16,15,13,9)の8個で循環、
• 18で割った余りは、
  • kが偶数のとき1が一度だけ、その後(2,4,8,16,14,10)で循環、
  • kが奇数のときこの他に17が一度だけ、
  合計8個が現れる。

よって、