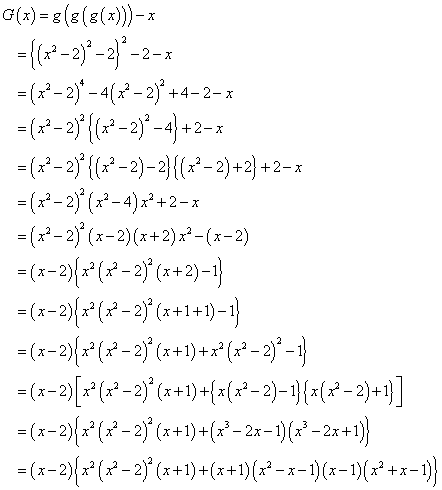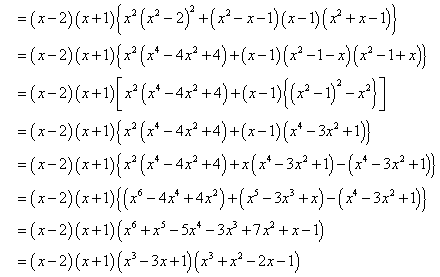xの2次関数g(x)について考える。
2次方程式g(x)-x=0が異なる2解u,vをもつとすると、
G(x)=g(g(x))-x
とおくとき、4次方程式G(x)=0は、u,vを解にもつ。
[証明]
g(u)-u=0
g(v)-v=0
G(u)=g(g(u))-u=g(u)-u=0
G(v)=g(g(v))-v=g(v)-v=0
したがって、G(x)は、2次式Q(x)を用いて次のように書ける。
G(x)={g(x)-x}・Q(x)
ここで、2つの異なる数、α,βが、
g(α)=β,g(β)=α
という関係をみたしているとする。
G(α)=g(g(α))-α=g(β)-α=α-α=0
G(β)=g(g(β)-β=g(α)-β=β-β=0
であるから、α,βは4次方程式G(x)=0の解である。
一方、
g(α)-α=β-α 0
0
g(β)-β=α-β 0
0
であるから、α,βは、2次方程式Q(x)=0の解でなければならない。
これは何を意味しているのか?
たった2つの要素をもつ集合U={α,β}に対して、UからUへの写像g(x)が
「上への写像」かつ「一対一対応」で、
なおかつ、g(x) x、決して自分自身に写すことなく、
x、決して自分自身に写すことなく、
こうしてg(x)によって、α,βが順次「循環的」に定義されるような、そんな、特別な数α,βのセットを知りたければ、
4次式G(x)=g(g(x))-xを、
2次式g(x)-xで割り算して、
商Q(x)を得れば、Q(x)=0の解が、ほかならぬα,βなのである。
[実験]
g(x)=x2-2
g(x)-x=x2-x-2=(x-2)(x+1)
G(x)=g(g(x))-x=(x2-2)2-2-x
=x4-4x2+4-2-x
=x4-4x2+2-x
=x2(x2-4)+2-x
=x2(x-2)(x+2)-(x-2)
=(x-2){x2(x+2)-1}
=(x-2){x2(x+1)+(x2-1)}
=(x-2){x2(x+1)+(x+1)(x-1)}
=(x-2)(x+1){x2+(x-1)}
=(x-2)(x+1)(x2+x-1)
x2+x-1=0の2つの解α,βを次のようにとれば、
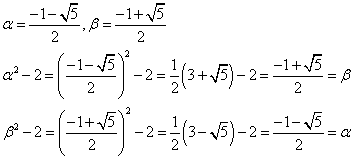
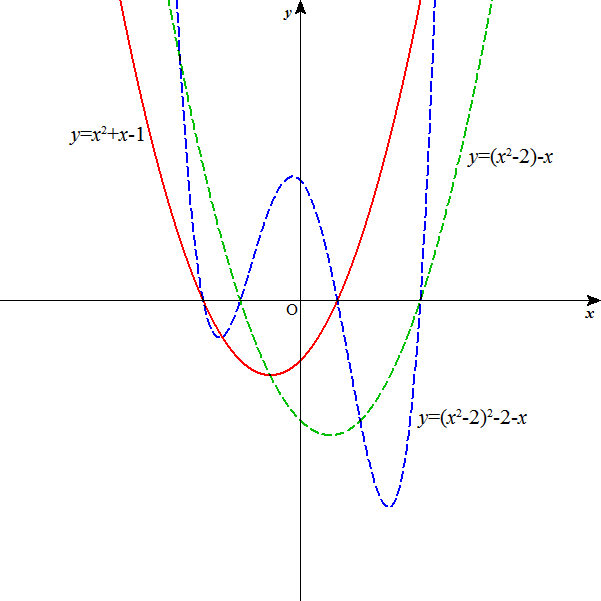
同様にして、
G(x)=g(g(g(x)))-x
とおくとき、8次方程式G(x)=0は、u,vを解にもつ。
[証明]
g(u)-u=0
g(v)-v=0
G(u)=g(g(g(u)))-u=g(g(u))-u=g(u)-u=0
G(v)=g(g(g(v)))-v=g(g(v))-v=g(v)-v=0
したがって、G(x)は、6次式Q(x)を用いて次のように書ける。
G(x)={g(x)-x}・Q(x)
ここで、3つの異なる数、α,β,γが、
g(α)=β,g(β)=γ,g(γ)=α
という関係をみたしているとする。
G(α)=g(g(g(α)))-α=g(g(β))-α=g(γ)-α=α-α=0
G(β)=g(g(g(β)))-β=g(g(γ))-β=g(α)-β=β-β=0
G(α)=g(g(g(α)))-γ=g(g(α))-γ=g(β)-γ=γ-γ=0
であるから、α,β,γは8次方程式G(x)=0の解である。
一方、
g(α)-α=β-α 0
0
g(β)-β=γ-β 0
0
g(γ)-γ=α-γ 0
0
であるから、α,β,γは、6次方程式Q(x)=0の解でなければならない。
これは何を意味しているのか?
たった3つの要素をもつ集合U={α,β,γ}に対して、UからUへの写像g(x)が
「上への写像」かつ「一対一対応」で、
なおかつ、g(x) x、決して自分自身に写すことなく、
x、決して自分自身に写すことなく、
こうしてg(x)によって、
例えば、g(α)=β,g(β)=γ,,g(γ)=αのように、
α,βが順次「循環的」に定義されるような、
そんな、特別な数α,β,γのセットを知りたければ、
8次式G(x)=g(g(x))-xを、
2次式g(x)-xで割り算して、
商Q(x)を得れば、6次方程式Q(x)=0の解のなかに、ほかならぬα,β,γが含まれているのである。
6次方程式には最大6個の解があるから、そのうちのどの3個を選んでも、よいように思えるから、一つの2次式g(x)に対して、6C3=20通りものα,β,γのセットが存在しうることになりそうであるが、これには、確信がもてない(笑)。
[実験]
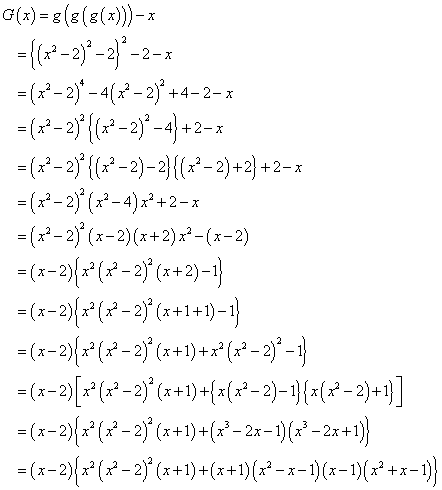
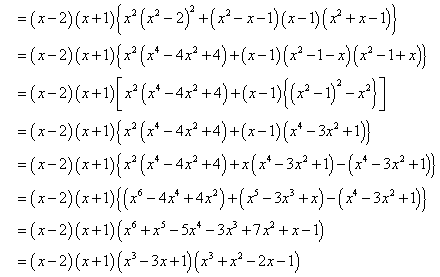
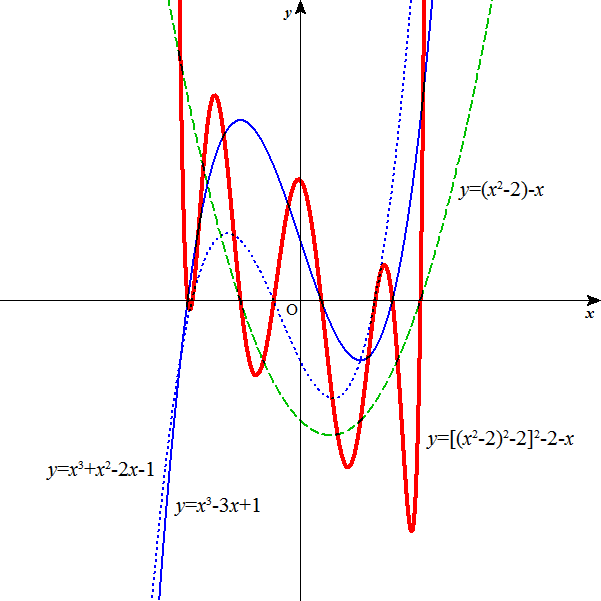
 0
0
 0
0
 x、決して自分自身に写すことなく、
x、決して自分自身に写すことなく、
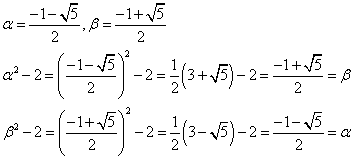

 0
0
 0
0
 0
0
 x、決して自分自身に写すことなく、
x、決して自分自身に写すことなく、