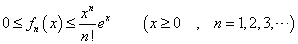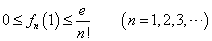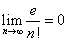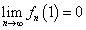- xのn次多項式f(x)を考える。これを順次、n回微分することで、各項の係数anを決定することが出来る。
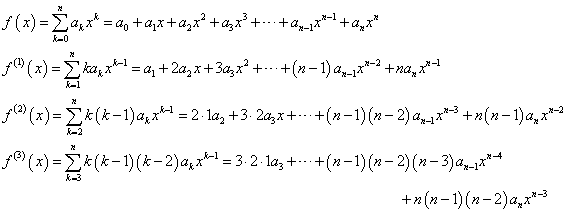
すなわち、
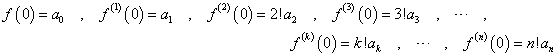
であるから、
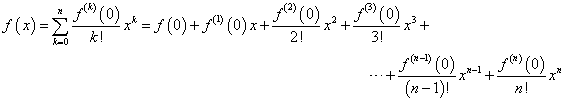
ということは、ある関数が、無限回微分可能であるとき、これを、n次多項式で「近似」出来ることがわかる。上のnはどこまでも引き延ばすことが出来るから、どこか「途中でやめた」とすれば、それは、「本当の値」とは、少しだけずれてしまうことになるからだ。こういうのを「テーラー級数展開」、または「マクローリン級数展開」による近似と呼ぶ。
- f(x)=exについて、マクローリン級数展開をほどこすと、
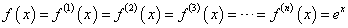
であるから、第n項(k=0,1,2,・・・n-1)までをとると、
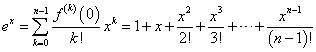
となる。
したがって、この問題で、fn(x)と呼ばれているのは、無限級数でしか表せないはずの、exを有限項、第n項までの多項式で「近似」した際の、「誤差」を表している。微分積分学では、これを「ラグランジュの剰余項」と呼んでいる!
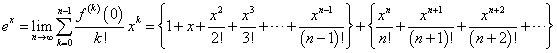
上式の二つめの{}が、その姿を表している。その部分を取り出して、次のように変形してみると、
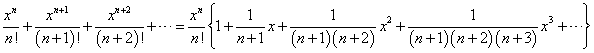
ここで、
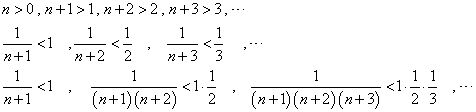
であるから、
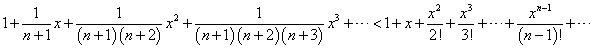
右辺は、無限項まで続く限り(!)、exに等しいから、
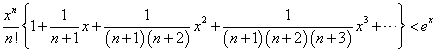
が得られる。一方、左辺は、x 0に対して、正または0である。
0に対して、正または0である。
さらに、上式にx=1を代入してみると、これは自然対数の底(ネイピア数)の近似式であって、
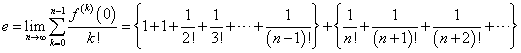
これを第n項までで止めたときの、「誤差」が、fn(1)なのであるから、nを無限にすれば0に収束するのは、それは「理の当然」なのであった。
ちなみに「ネイピア数」の級数展開による近似値は、こんな感じで、とても収束が速く、第8項くらいで十分に使い物になる値である。
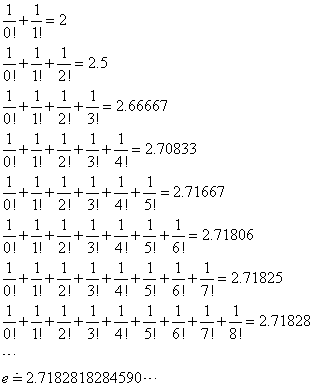
この問題は、このようにして(笑)作成された。でも、高校生が、こんな答案を書くわけにはいかないから、何も知らない振りをして、「数学的帰納法」などを用いて、解くことになる。
。
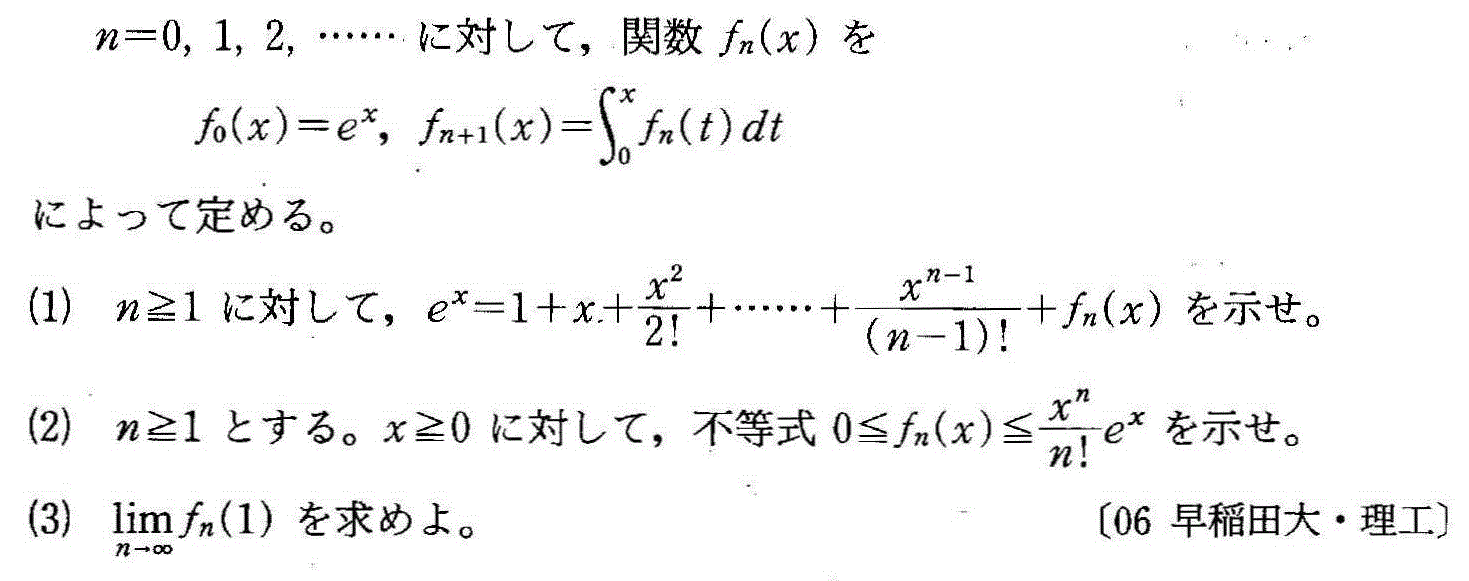
- [1]
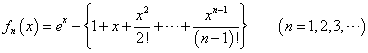 ・・・(*)
・・・(*)
であることを示したい。
- n=1のとき
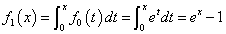
成立する。
- n=kのとき、(*)が成立すると仮定する、すなわち、
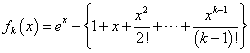
と仮定する。
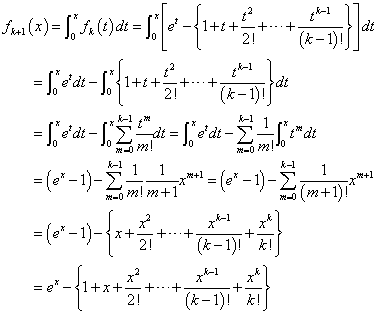
となり、n=k+1のときも成立する。
i,iiより、n=1,2,3,・・・に対して、(*)が成立する。
- [2]
まず、
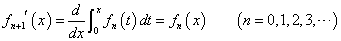 ・・・(1)
・・・(1)
である。
(ア) x 0に対して、fn(x)
0に対して、fn(x) 0 (n=1,2,3,・・・)を示したい。
0 (n=1,2,3,・・・)を示したい。
- n=1のとき、f1(x)=ex-1 であるから、
x 0に対して、ex-1
0に対して、ex-1 0
0
成立する。
- n=kのとき、x
 0に対して、fk(x)
0に対して、fk(x) 0 と仮定する。
0 と仮定する。
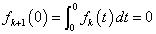 ・・・(2)
・・・(2)
(1)式と、仮定より、、
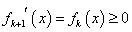 ・・・(3)
・・・(3)
(2)(3)式より、
x 0に対して、fk+1(x)
0に対して、fk+1(x) 0
0
となり、n=k+1のときも成立する。
i,iiより、x 0に対して、fn(x)
0に対して、fn(x) 0 (n=1,2,3,・・・) が成立する。
0 (n=1,2,3,・・・) が成立する。
(イ) x 0に対して、
0に対して、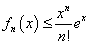 (n=1,2,3,・・・)を示したい。
(n=1,2,3,・・・)を示したい。
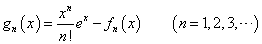 とおく。
とおく。
- n=1のとき
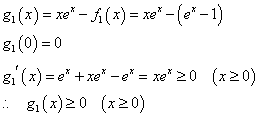
- n=kのとき
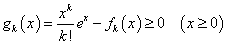
と仮定する。
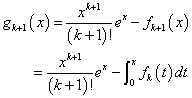
であるから、
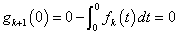 ・・・(4)
・・・(4)
また、
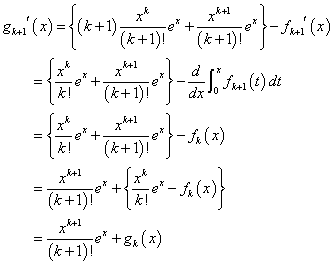
であるから、仮定より、 x 0に対して、
0に対して、
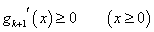 ・・・(5)
・・・(5)
(4)(5)式より、
x 0に対して、gk+1(x)
0に対して、gk+1(x) 0
0
となり、n=k+1のときも成立する。
i,iiより、 x 0に対して、
0に対して、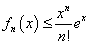 (n=1,2,3,・・・)が成立する。
(n=1,2,3,・・・)が成立する。
- [3]
[2]より、
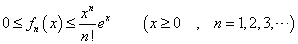
であるから、
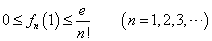
ここで、
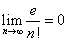
であるから、「はさみうちの原理」より、
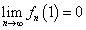
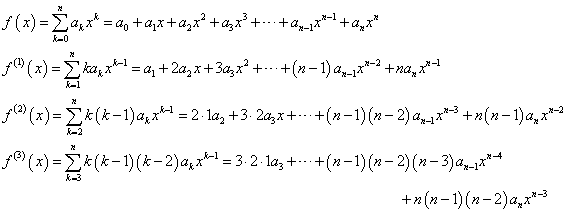
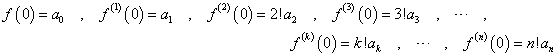
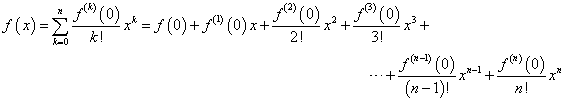
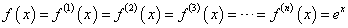
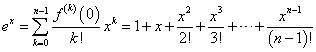
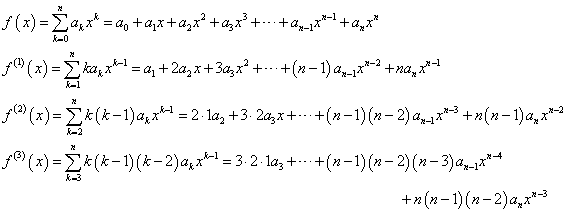
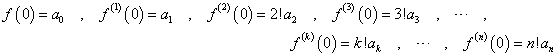
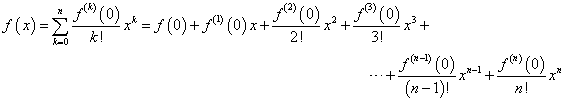
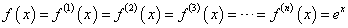
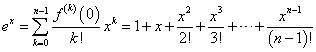
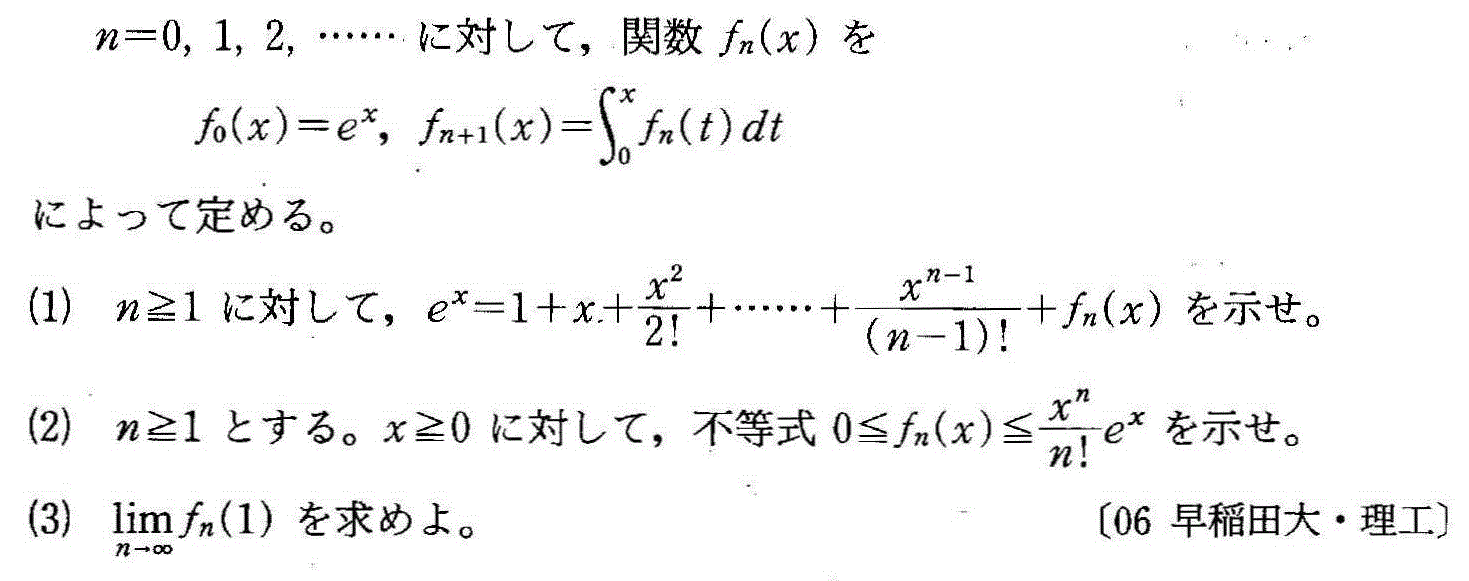
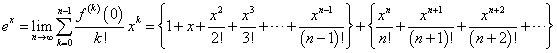
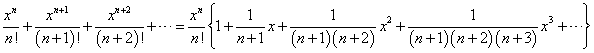
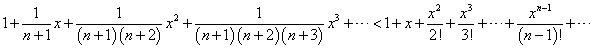
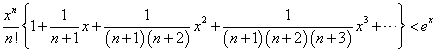
 0に対して、正または0である。
0に対して、正または0である。
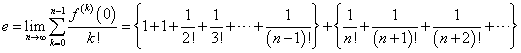
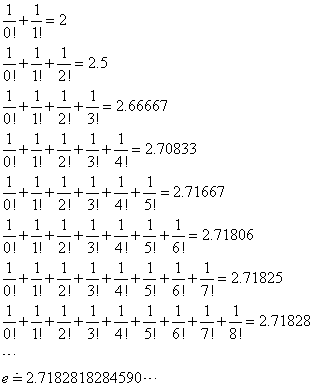
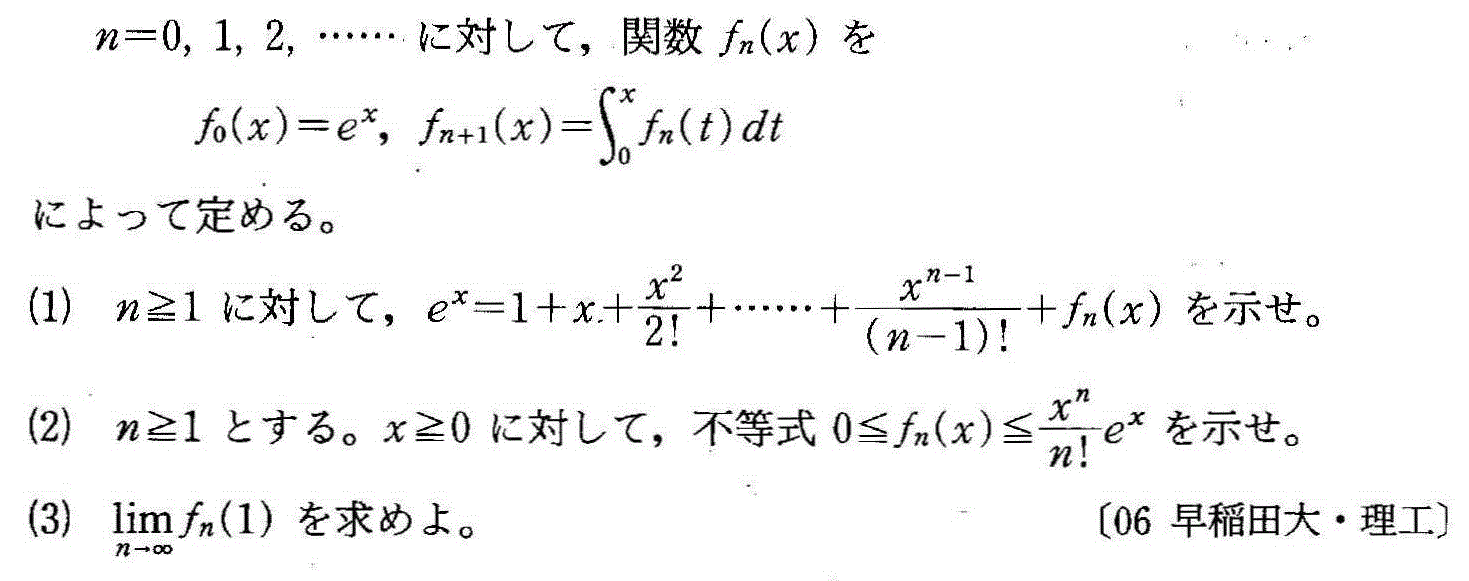
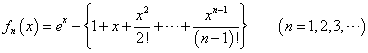 ・・・(*)
・・・(*)
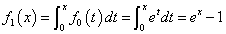
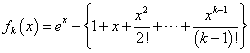
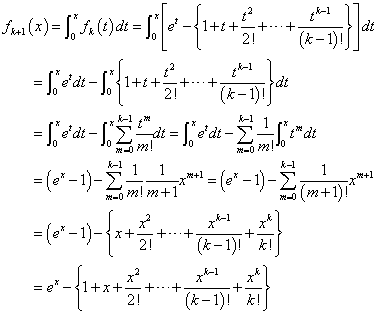
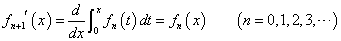 ・・・(1)
・・・(1)
 0に対して、fn(x)
0に対して、fn(x) 0 (n=1,2,3,・・・)を示したい。
0 (n=1,2,3,・・・)を示したい。
 0に対して、ex-1
0に対して、ex-1 0
0
 0に対して、fk(x)
0に対して、fk(x) 0 と仮定する。
0 と仮定する。
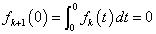 ・・・(2)
・・・(2)
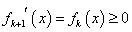 ・・・(3)
・・・(3)
 0に対して、fk+1(x)
0に対して、fk+1(x) 0
0
 0に対して、fn(x)
0に対して、fn(x) 0 (n=1,2,3,・・・) が成立する。
0 (n=1,2,3,・・・) が成立する。
 0に対して、
0に対して、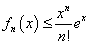 (n=1,2,3,・・・)を示したい。
(n=1,2,3,・・・)を示したい。
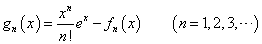 とおく。
とおく。
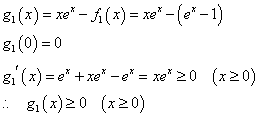
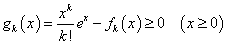
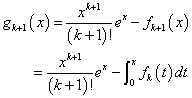
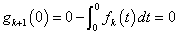 ・・・(4)
・・・(4)
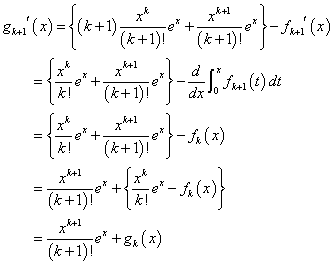
 0に対して、
0に対して、
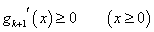 ・・・(5)
・・・(5)
 0に対して、gk+1(x)
0に対して、gk+1(x) 0
0
 0に対して、
0に対して、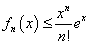 (n=1,2,3,・・・)が成立する。
(n=1,2,3,・・・)が成立する。