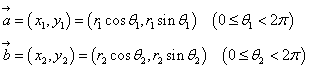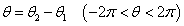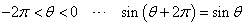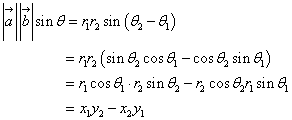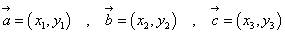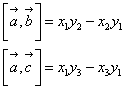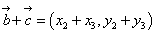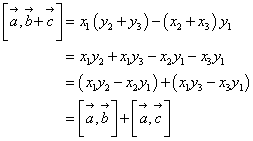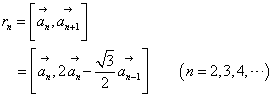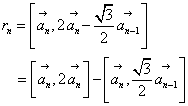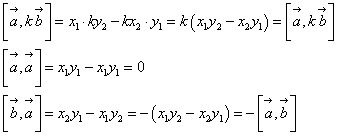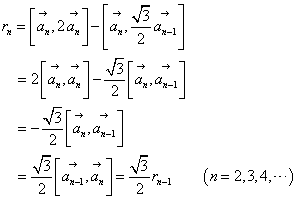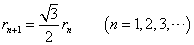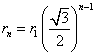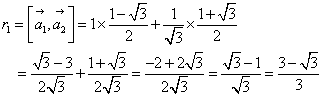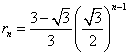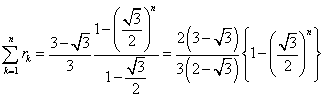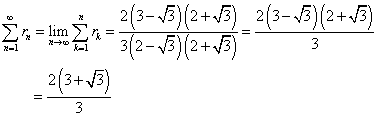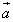 ,
,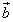 ]は、
]は、
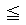 θ
θ  π
ならば、sinθ
π
ならば、sinθ 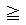 0 だから、「面積」とも「大きさ」とも呼べるが、
0 だから、「面積」とも「大きさ」とも呼べるが、
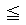 θ
θ  2π
では、sinθ
2π
では、sinθ 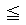 0 と、不の値になってしまうから、「面積」、「大きさ」とは呼べない。
0 と、不の値になってしまうから、「面積」、「大きさ」とは呼べない。
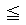 θ
θ  π
π
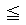 θ
θ  2π
2π
|
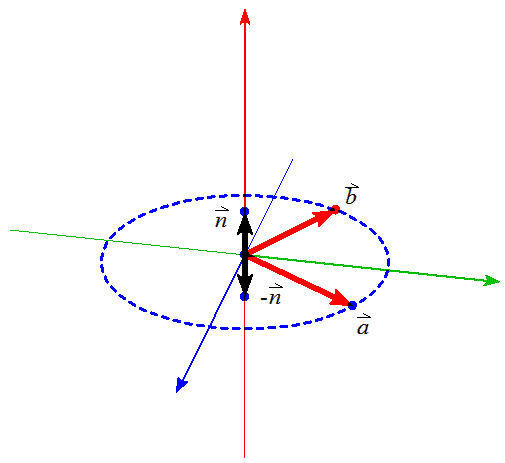
ベクトルの外積
ベクトルa,bのなす角をθとすると、 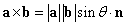
ただし、nは、aがbに重なるように最小の角度で回転したとき、 その回転を右ねじの回転とみなして、右ねじの進む方向の単位ベクトル |
x,y,z各方向の単位ベクトルをそれぞれi,j,kとすると、
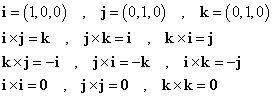
|
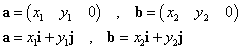
とすると、 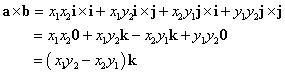
右辺は、a,bをそれぞれ行ベクトルとする2次の正方行列 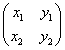 の行列式であるから、 の行列式であるから、
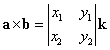
kは単位ベクトルであるから、 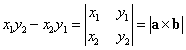
|
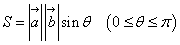
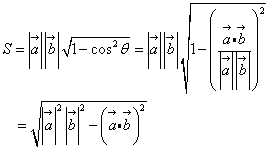
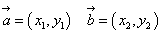
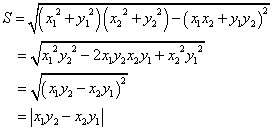
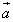 ,
,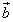 のそれぞれが、x軸となす角のうち、どちらが大きいか?、とか、その差がπより大きいか?、などという面倒なことを考えずに済む方法はないだろうか?
のそれぞれが、x軸となす角のうち、どちらが大きいか?、とか、その差がπより大きいか?、などという面倒なことを考えずに済む方法はないだろうか?