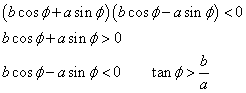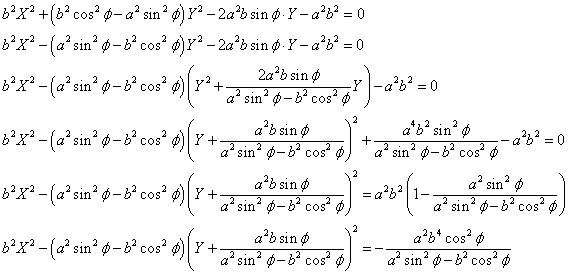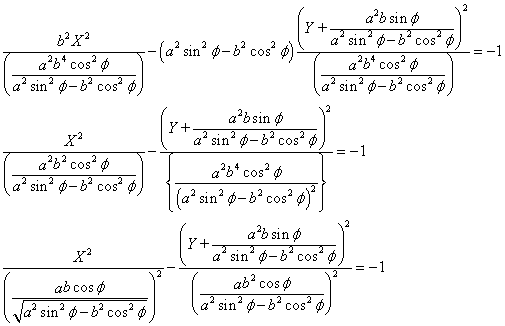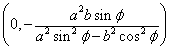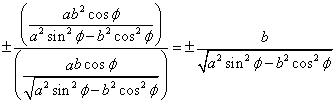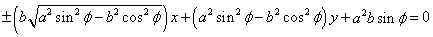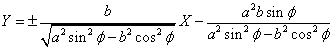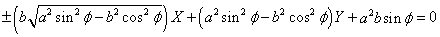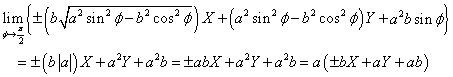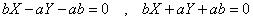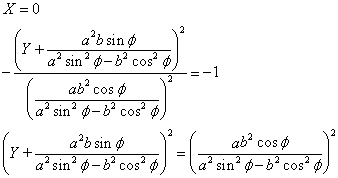- x,yの2次式、すなわち、
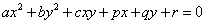
で表される曲線群は、「2次曲線」と呼ばれ、
円、楕円、放物線、双曲線、直線、など、さまざまな図形をあらわすことが知られている。
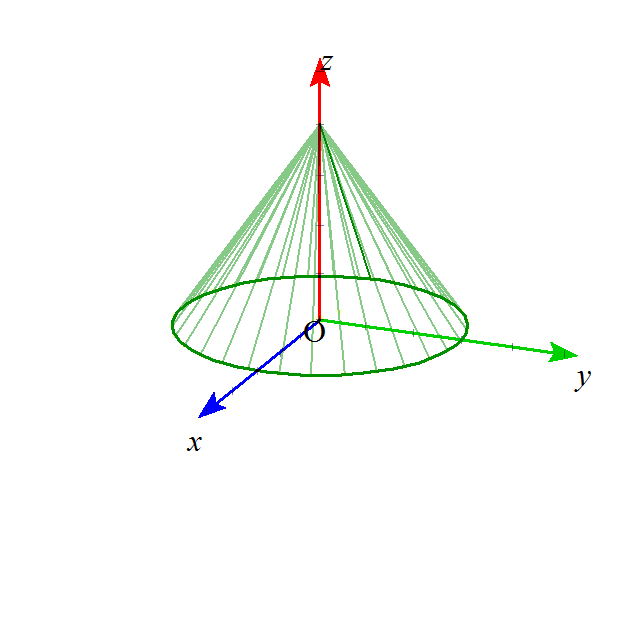
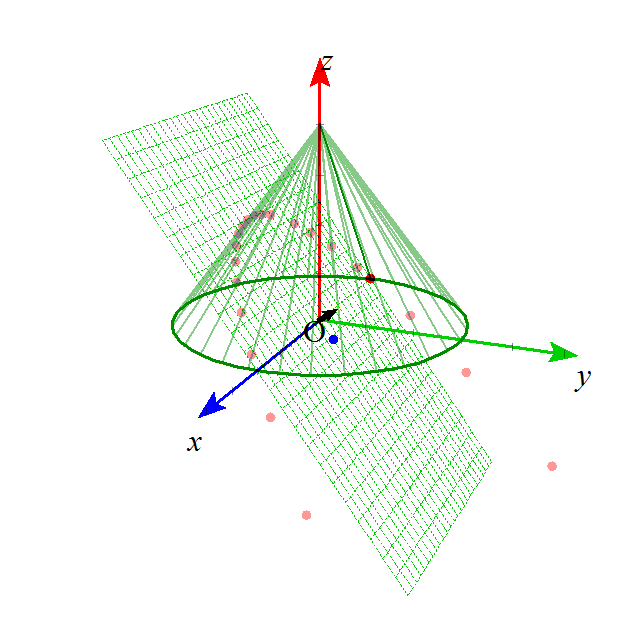
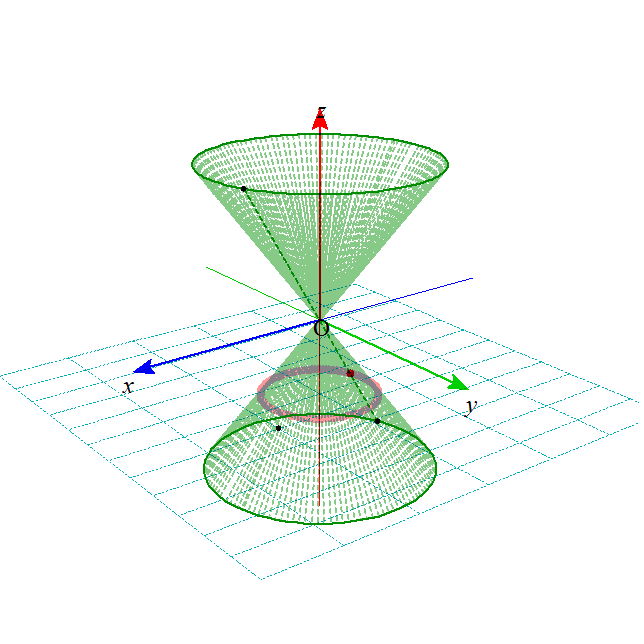
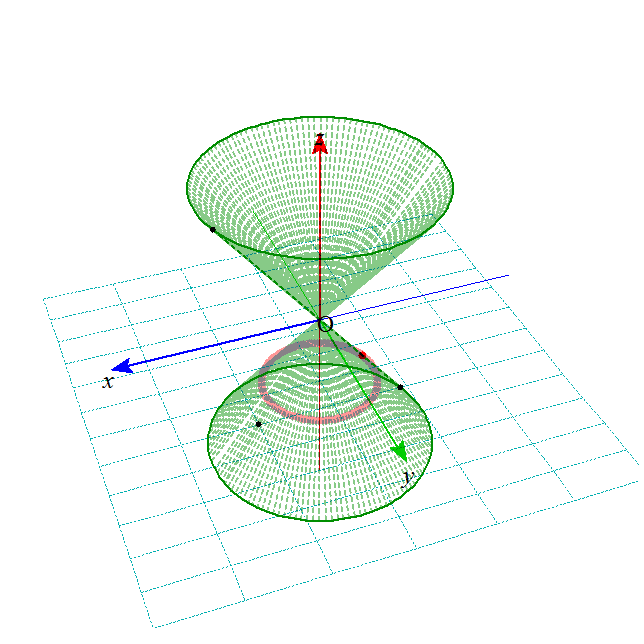
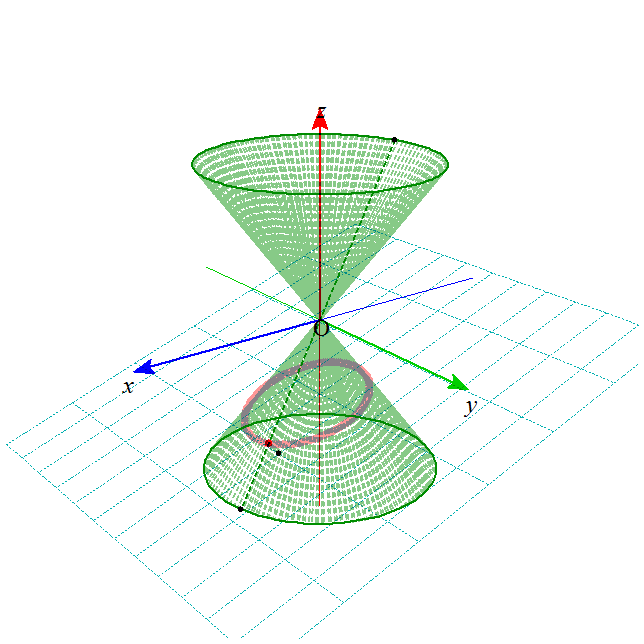
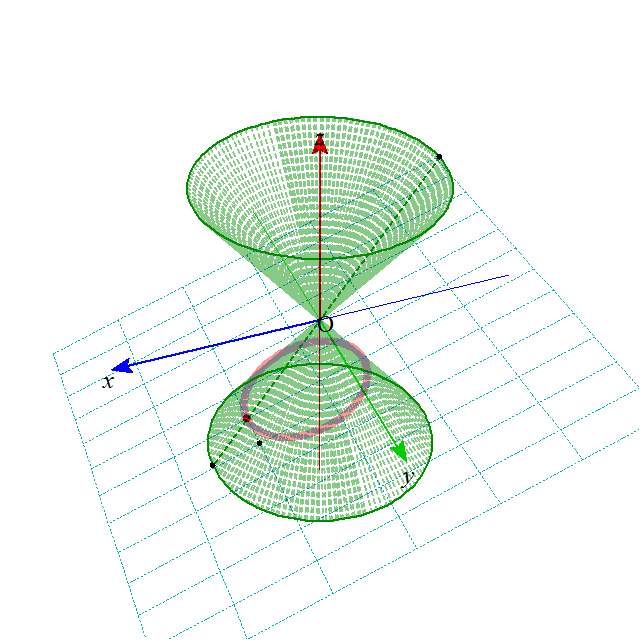
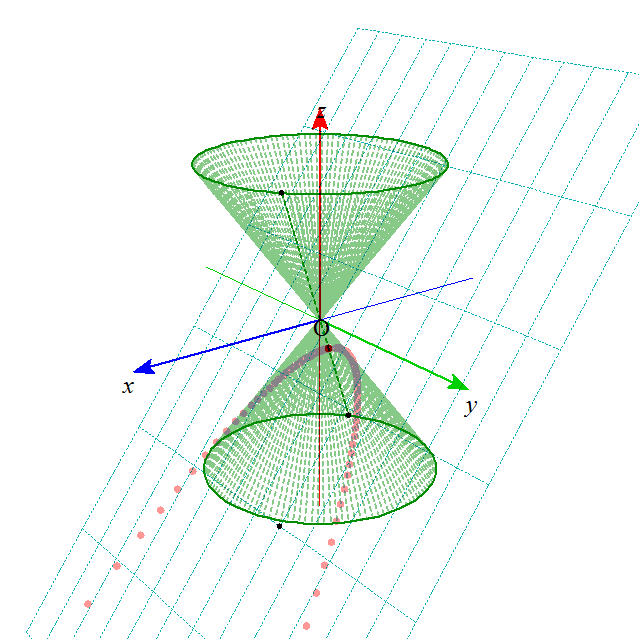
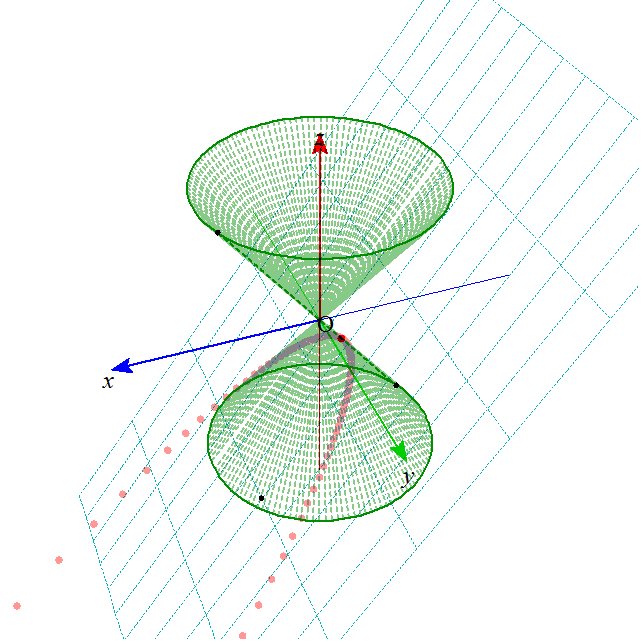
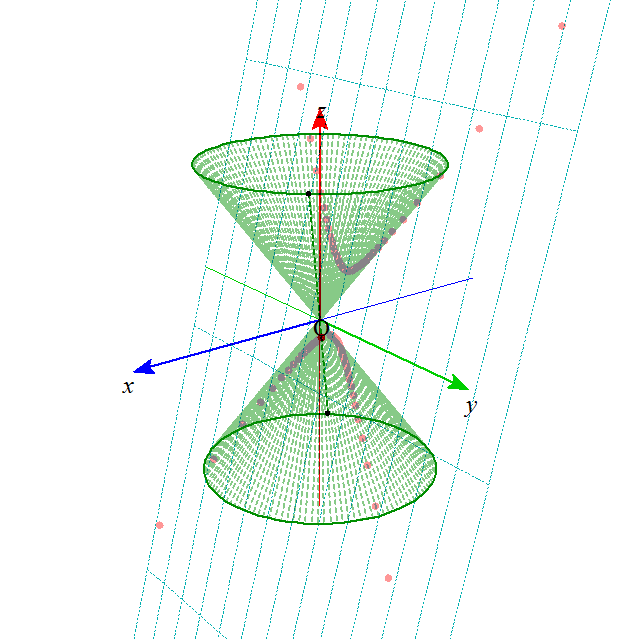
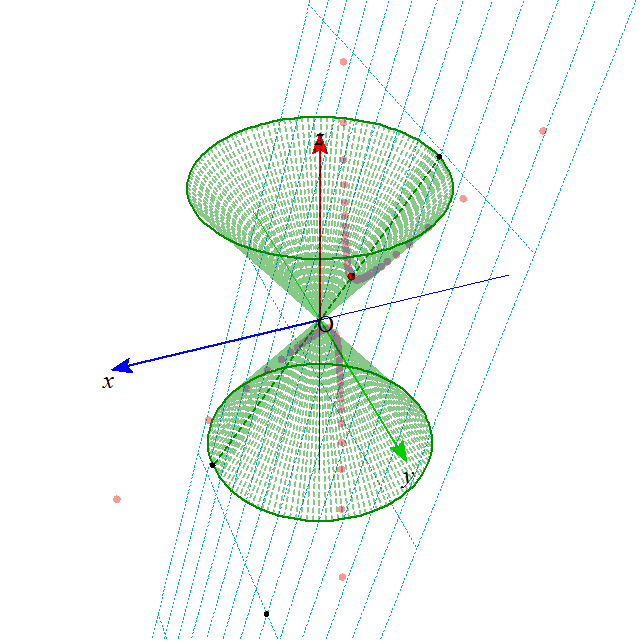
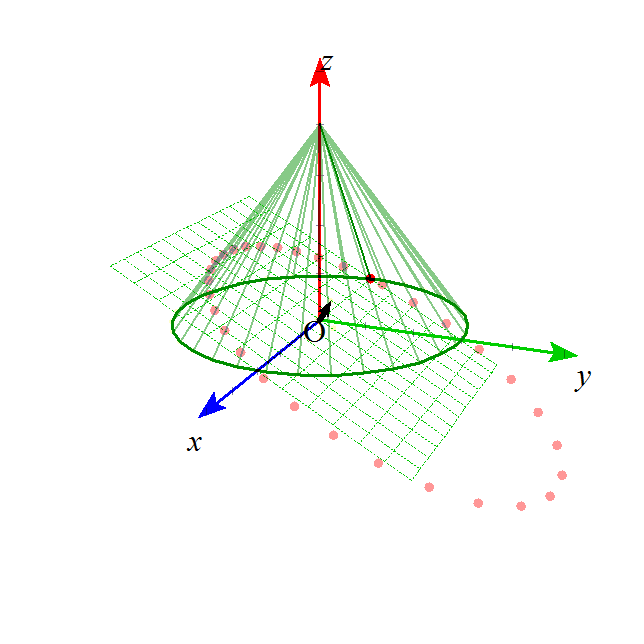
- これらの図形は、下の図のような、無限に広がる円錐の側面を、ある平面で切った切り口として、ことごとく表されることから、
「円錐曲線」とも呼ばれる。
- まず、円錐の底面に平行な平面で切ると、円が得られる。
- この平面を少し傾けていくと、まず、さまざまな楕円となり、
- ちょうどその平面から最も近い円錐の「母線」と平行になったとき、楕円は「千切れ」、一か所だけ放物線となる瞬間がある。
- ここからさらに傾けていくと、平面が円錐の底面と垂直になるにいたるまで、さまざまな双曲線が得られる。
もし、円錐の中心軸上の点を中心に平面を傾けていたのなら、双曲線は、最後には互いに交わる2直線となる。
ここでは、
- 円錐の中心軸上の点を中心に平面を、底面に平行な状態から、底面に垂直な状態に至るまで、順次傾けていったとき切り口として得られる図形の方程式
- xyの項を含む2次曲線の式を、1次変換によって、これを含まない式に変形する方法
- 「円錐曲線」を、定点(焦点)との距離の定直線(準線)への距離に対する比(「離心率」という)、によって分類し、統一的な式で表現する方法、その極座標形式
- 「円錐曲線」の例として、万有引力によって運動する惑星の軌道が、円、楕円、放物線、の各2次曲線によって表現されること
について考えることにする。
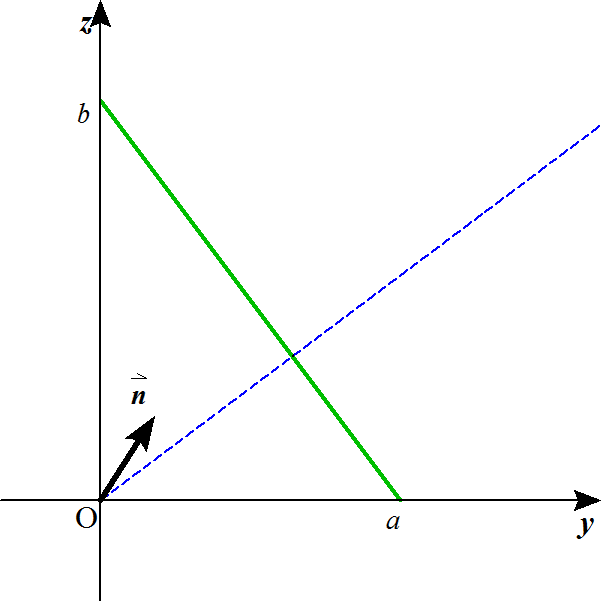
xy平面上の、原点中心、半径aの円を底面とし、(0,0,b)を頂点とする円錐Vを考える。
(a 0,b
0,b 0)
0)
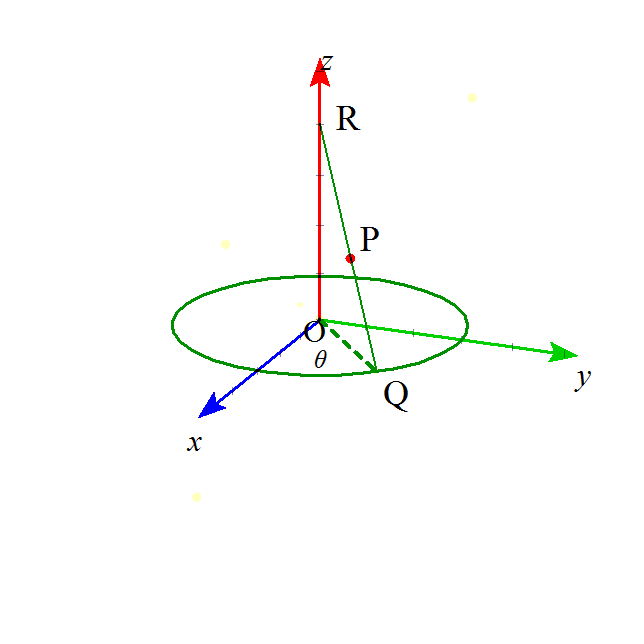 Q(acosθ,asinθ,0) (0
Q(acosθ,asinθ,0) (0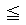 θ
θ 2π)
2π)
R(0,0,b)
とすると、円錐の側面上の任意の点Pは、
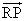 =t
=t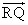 (tは任意の実数)
(tは任意の実数)
と表すことができる。
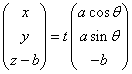 したがって、
したがって、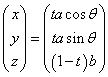 次に、原点を通り、yz平面上の単位ベクトル
次に、原点を通り、yz平面上の単位ベクトル
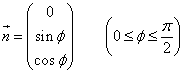

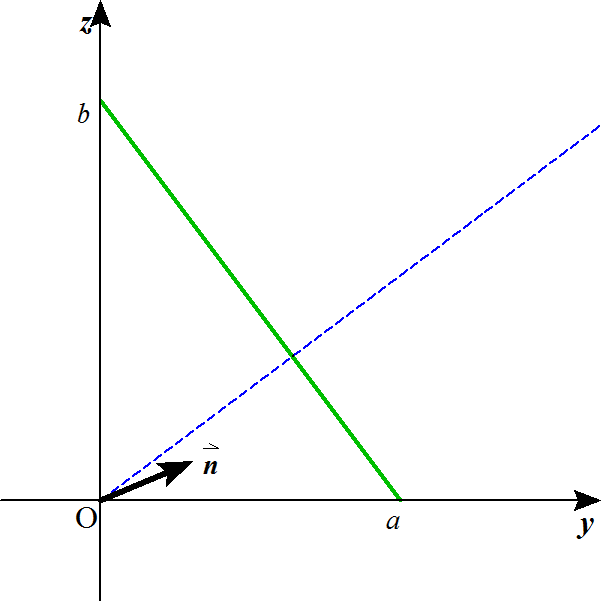
を法ベクトルとする平面αを考える。
αの方程式は、
 すなわち、
すなわち、
α : 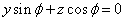
である。
Vとαとの交線を求めたい。
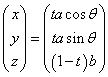 を
を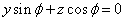 に代入して、
に代入して、
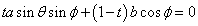
すなわち、
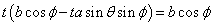
tについて解くと、
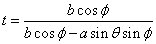
よって、
 次に、平面α上に、次のようなXY座標をとる。すなわち、
次に、平面α上に、次のようなXY座標をとる。すなわち、
- X軸は、x軸である。
- y軸を平面αに投影したものがY軸である。
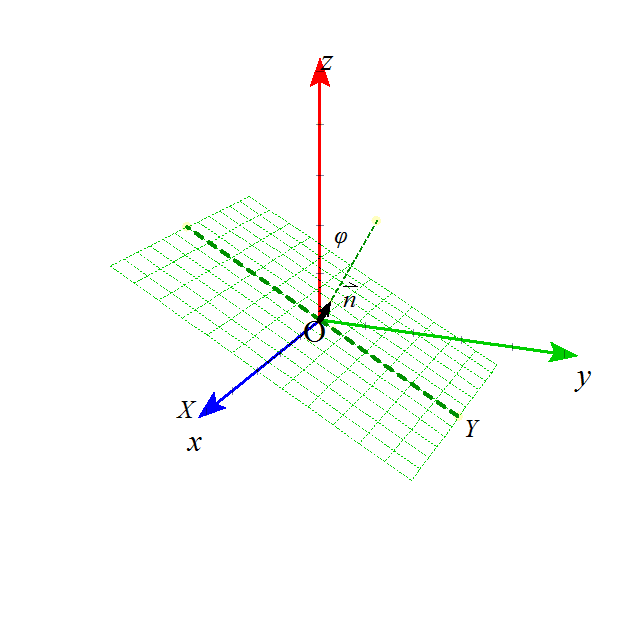

yz平面上の点(y,z)は、Y軸上の
ycosφ-zsinφ
に投影される。
すなわち、変換、
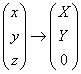 において、
において、
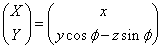 である。すなわち、
である。すなわち、

平面αを決定すれば、φは決まる。定数φに対して、θを媒介変数とするXY平面上の曲線が、Vのαによる切り口である。
θを消去する。

これは、cosθ,sinθに関する連立1次方程式であるから、

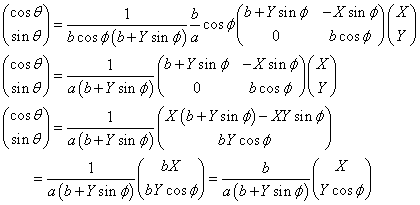
こうして、
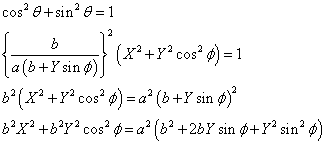
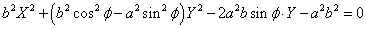 ・・・(1)
・・・(1)
が得られた。
ここで、Y2の係数について、分類する必要が生じる。
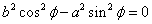 のとき
のとき
すなわち、
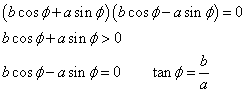
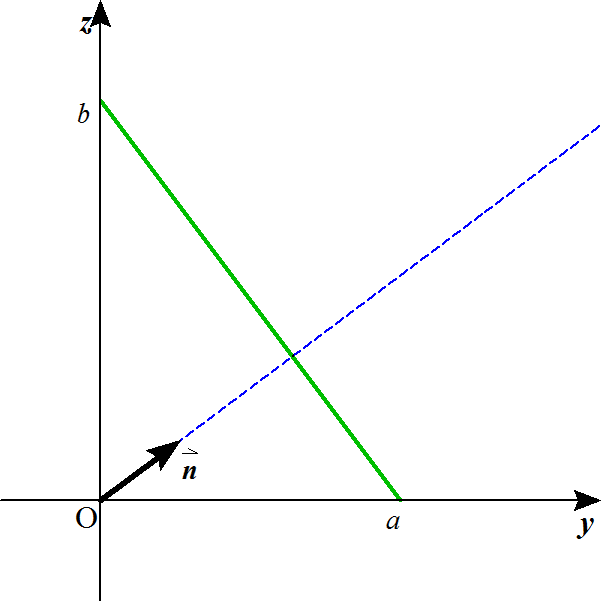
これは、母線に平行な平面αで切る場合にあたる。
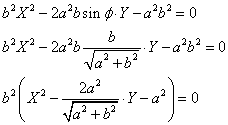
これは、放物線である。
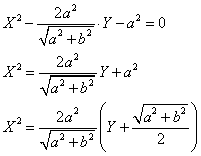
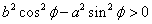 のとき
のとき
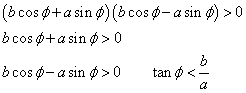
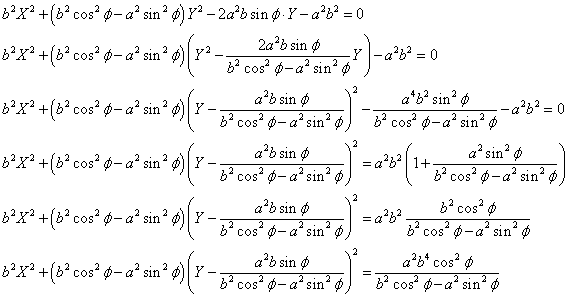
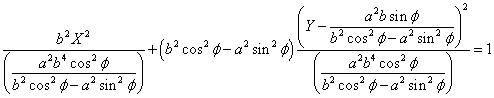
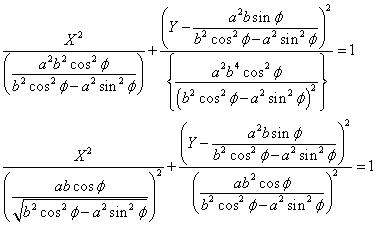
これは、楕円である。
(特にφ=0のとき、中心(0,0),半径aの円である。)
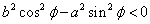 のとき
のとき
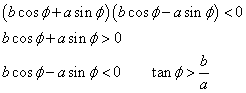
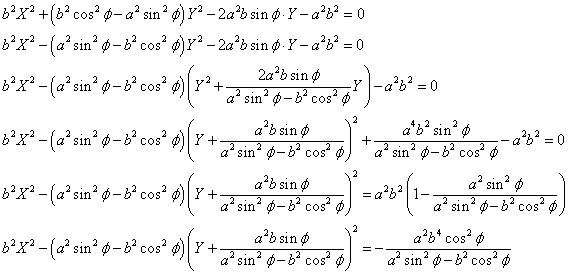
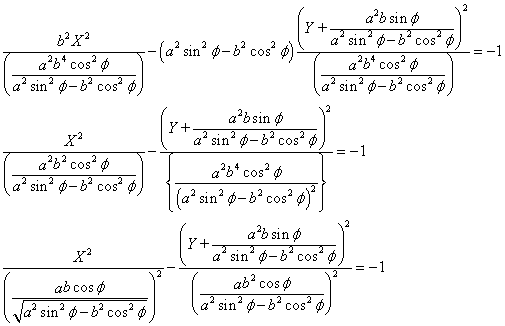
これは、双曲線である。
| 中心 | 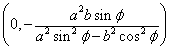 |  |
漸近線の傾き
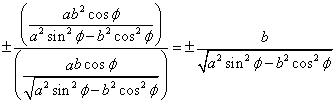
したがって漸近線の方程式は、
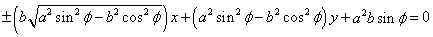
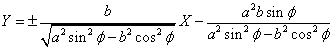
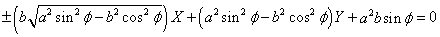
この式の左辺は、φ→π/2で、次のようになるから、
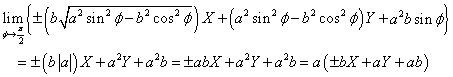
円錐の底面の中心を通り、底面に垂直な平面で切った場合、双曲線は、次のような2直線に収束する。
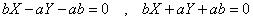
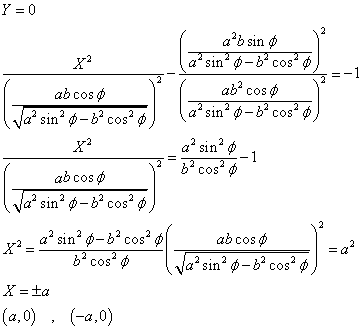
X軸との交点
Y軸との交点
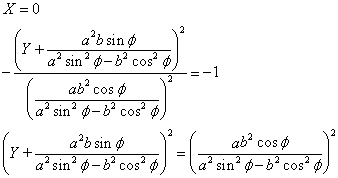

特にφ=π/2のとき、2直線を表す。


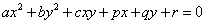
 0,b
0,b

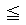 θ
θ 2π)
2π)
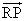 =t
=t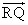 (tは任意の実数)
(tは任意の実数)
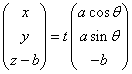 したがって、
したがって、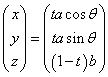
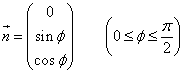

 すなわち、
すなわち、
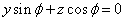
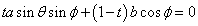
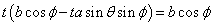
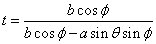



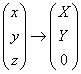 において、
において、
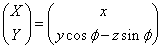 である。すなわち、
である。すなわち、



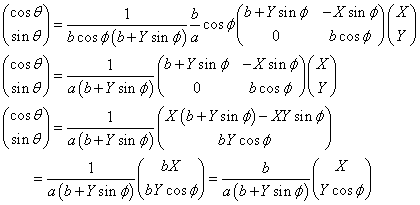
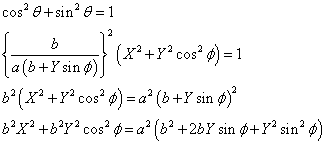
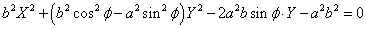 ・・・(1)
・・・(1)
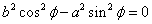 のとき
のとき
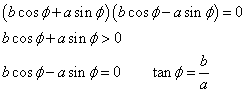

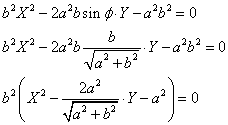
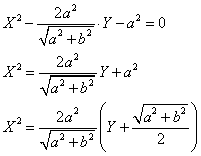

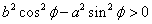 のとき
のとき
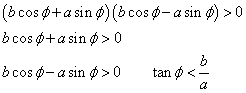

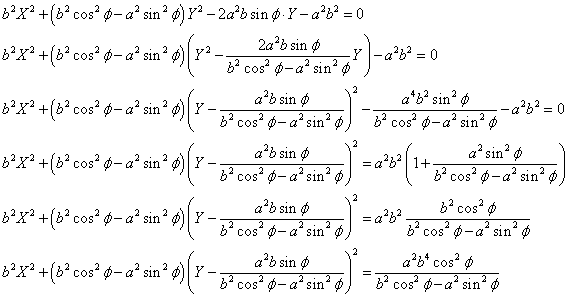
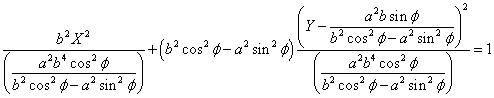
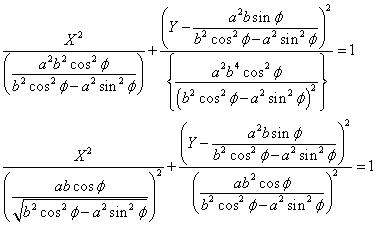

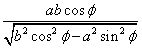
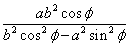
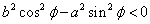 のとき
のとき