---

1. xをyの関数であらわす。
     
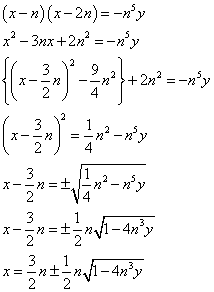
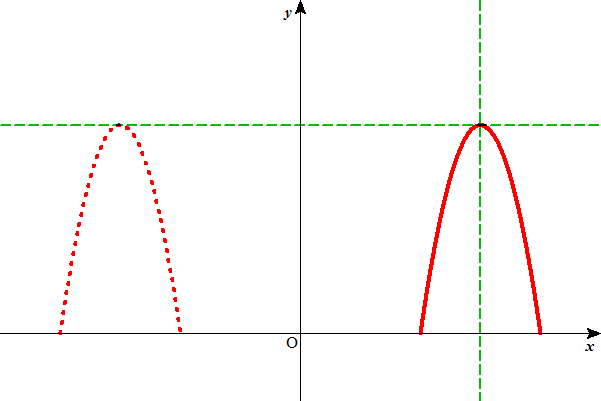
   したがってy軸まわりの回転体の体積V_nは、
   
   
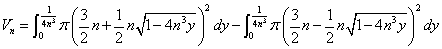
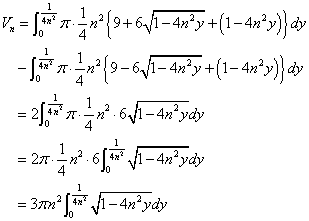
   置換積分を行って、
   
2. したがって、
   
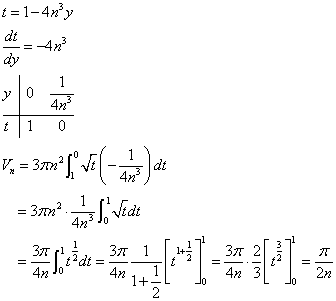
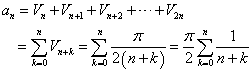
   よって(区分求積法)、
   

---

[別解](「バームクーヘン」型積分)

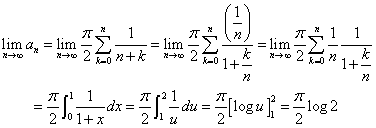
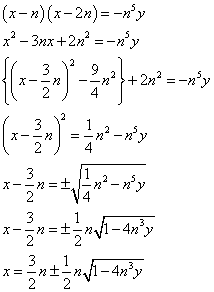
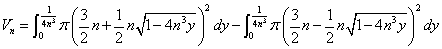
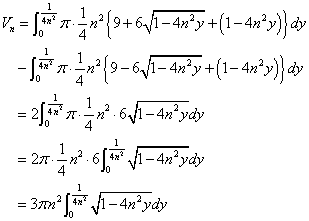
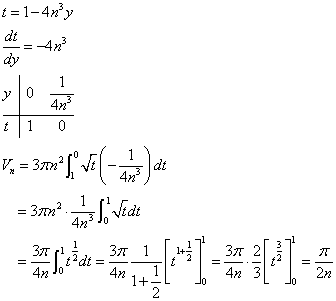
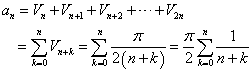
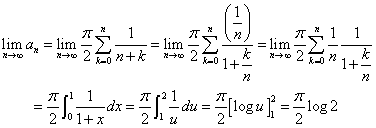
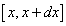1. 上の関数の、区間部分をy軸まわりに回転して得られる立体は、厚さdxの円筒である。
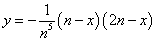   これを「展開」すると、縦、横2πx、高さdxの直方体となる。
   この直方体を、x軸方向に積み上げて（xで「積分」して）、求める立体の体積を得ることが出来る。
   
   置換積分を行って、
   

---

[参考]

有限個のnについて、収束の様子を調べてみた。

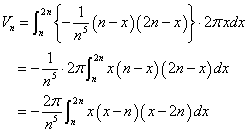
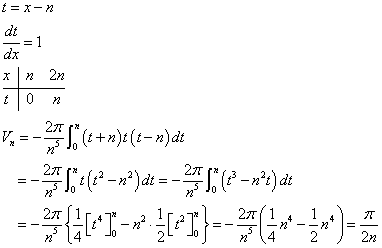
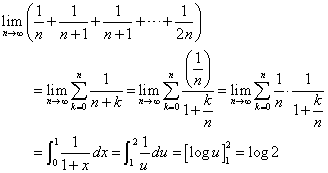
n	1/n+1/(n+1)+・・・+1/2n	log2
2	1.08333333333333333	0.693147180559945309
5	0.845634920634920635	0.693147180559945309
10	0.768771403175427943	0.693147180559945309
100	0.700653430481824215	0.693147180559945309
1000	0.693897243059937497	0.693147180559945309
10000	0.693222181184945308	0.693147180559945309
100000	0.693154680566195307	0.693147180559945309