---

• (1) 任意の自然数nに対して、
  
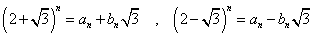
  となる自然数の数列、a_n,b_nが存在することを示したい。
  1. n=1のとき    a₁=2  ,  b₁=1
  2. n=kのとき    
     
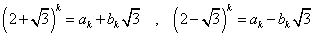
     となる自然数の数列、a_k,b_kが存在すると仮定する。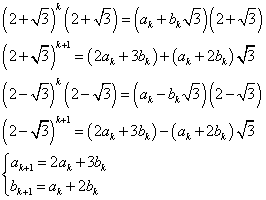
     
     ここで、a_k,b_kは自然数であるから、a_k+1,b_k+1も自然数である。
     n=k+1のときも成立する。
  i,iiより、任意の自然数に対して、
  
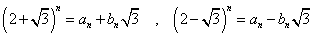
  となる自然数の数列、a_n,b_nが存在することが示された。
• (2)自然数nに対して、
  
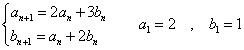
  であるとき、任意の自然数nに対して、
  a_n²-3b_n²=1
  が成立することを示したい。
  1. n=1のとき    a₁²-3b₁²=2²-3×1²=1
  2. n=kのとき
     a_k²-3b_k²=1
     と仮定する。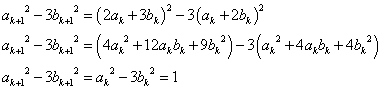
     
     n=k+1のときも成立する。
  i,iiより、任意の自然数に対して、
  a_n²-3b_n²=1
  が成立する。
• (3)
  (1)より、a_nは任意の自然数nに対して、自然数であるから、
  
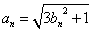
  ここで、b_nも任意の自然数nに対して、自然数であるから、
  3b_n²+1
  も自然数である。そこで、自然数mを、
  m=3b_n²+1
  とおけば、
  
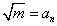
  また、
  m-1=3b_n²
  であるから、
  
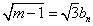
  したがって、このような自然数mに対して、
  
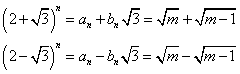
  が成立する。