1回の試行では、ある事柄が発生する確率がつねに一定値pであるような試行を、n回繰り返すことを考える。
n回中何回、その事柄が生じるかをXという変数で表すことにすると、
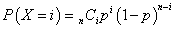
n回のうちi回のみ、その事柄が生じた、すなわち、残りn-i回は、生じなかった、n回のうち、どのi回であるかにはnCi通りの可能性がある。
このような式で表すことができる事態を、その確率変数Xは、二項分布B(n,p)に従う、と称す。発生するか、または、発生しないか、なる「二項」に着目していることからの命名であるが、二項定理、
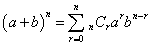
で、a=p,b=1-pとすれば、二項定理は、もちろん、任意の数a,b、任意の自然数nに対して成立する恒等式であるから、上の確率を、i=0,1,2,・・・,nについて足し合わせた、すべての場合の確率は、
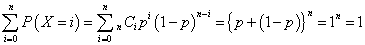
という当然の結果となる。
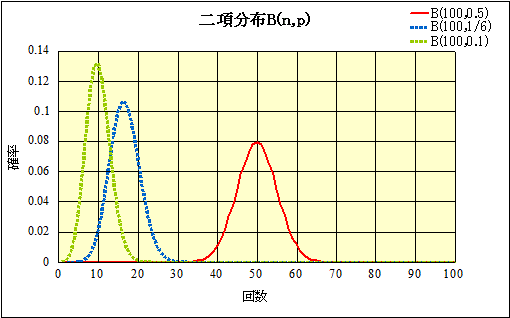
例を挙げる。B(100,0.5)、B(100,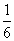 )、B(100,0.1)、のグラフを作ってみた。
)、B(100,0.1)、のグラフを作ってみた。
B(100,0.5)、は一回の試行である事柄が生ずる確率が0.5であるような試行を100回繰り返したときに、何回「それ」が生じるか?、であるから、たとえば、100回コインを投げて、何回「表が出るか」が例えになる。コインの表と裏は、特に異なる理由が「ない」から、およそ半分くらいは表が出るだろう、50がピークになるのは、当然、頷けるのである。
同様に、B(100,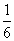 )、は、サイコロを100回投げて「6」が出る回数、と例えてよい。
)、は、サイコロを100回投げて「6」が出る回数、と例えてよい。
B(100,0.1)、ならば、デジタル式のストップ・ウオッチをスタートさせてから、好きなときに、止める。そのときに秒を表す1の位の数字は、「0,1,2,・・・,9」のいずれかの筈であるから、そんな試行を100回も繰り返してみる人は、事実としては余りいそうにはないのだが(笑)、そうしたときに、そのうち例えば他ならぬ「7」である回数を調べている、と見てよい。
ここでそれぞれ「コインの表」、「サイコロの6の目」、「秒針の1の位が7」といったのはすべて「恣意的」であるが、それが恣意的で「かまわない」ことを保証しているのが、「エルゴード性」であって、コインの「表/裏」、サイコロの「1,2,3,4,5,6」、秒針の1の位の「0,1,2,3,4,5,6,7,8,9」の間には、それぞれ、「特に異なる理由がない」から、その場合の数、2,6,10の逆数を以て、等確率pと断定しているのである。
「期待値」というのは、もし100回これらの試行を行ってみて、どのくらいの回数しかるべき事態が生じることが期待できるか?、の「目安」であって、誰も実際に100回試行を行う必要はなく、コインならば半分くらい、50回、サイコロならば6分の1、16.666・・・回、秒針の1のくらいなら、10分の1で、10回、・・・、といえるだろう。グラフのそれぞれの「ピーク」をなしている値がそれを示している。
ところが、この「ピーク」が、この「特に区別することのできない」場合の数が、2,6,10と次第に増えるにしたがって、左に遷移するにつれて、「高く」なっていくのは、どう「理解」したらよいのだろう?
コインを100回投げたら、ちょうど50回表が出ることよりも、サイコロを100回投げて「6」がちょうど16.666・・・回出ることの方が、さらに、100回止めたストップ・ウォッチの秒針が「7」を示している事の方が、「起こりやすい」ことを、説明してくれるような、私たちの「経験」上の対応物は、あるのだろうか?
上のグラフの曲線下の「面積」は、離散変数である「回数」を極限化して連続変数にすれば、それは「積分」と呼ばれるものになるが、・・・、横軸「回数」、縦軸「確率」で、「確率」には「回数/回数」で「次元」がないから、「面積」、縦と横の長さの積、という「アナロジー」を採用すれば、「回数」を表していることになる。いずれも100回しか試行していないのだから、どのグラフの曲線下の面積も等しく100である。ならば、「ピーク」が左に遷移するほどに、もし、同様の釣鐘型の左右対称な、縦と横の尺度を度外視して「相似」な形状のグラフであるならば、その「ピーク」は高くなり、かつ、「裾野」は狭い、尖った分布形になる。
それを示す指標が「分散」、ないしは、「標準偏差」で、「分散」は、各データとその「期待値」との差の2乗の、平均値である。各データが「期待値」と離れていればいるほど、「裾野」は広くなるだろうから、これは分布の「広がり方」の大きさを表すことになる。この例ならば、コイン、サイコロ、ストップ・ウォッチの順に、「分散」は、小さくなる筈である。ところが「分散」の次元は、定義上「回数の2乗」であって、私たちはそんなものを評価する「物差し」を持たない。「年齢」や「身長」を二乗した数値の「意味」がわからないだろうのと、同様である。そこで「分散」の正の平方根を持って「標準偏差」と称す、これは「回数」の次元を持つから、上のグラフの横軸上に、プロットする、ことが可能なのである。期待値の回りのたとえば、1標準偏差のレンジ、期待値をm、標準偏差をσと呼べば、m-σとm+σの間に含まれるデータ数がほぼ等しいであろうと推定されることで、釣鐘の「裾野」の広がりを表示する指標となりうるのである。
これだけの「前置き」をしないと、これから行う数式変形の「意味」を「説明」できないのである。誰に対してでもない、「自分」に対して(笑)。
本当は、生きていくのが「恐く」て仕方がない。いっそ死んでしまいたい、と一日に数十回は思う。ずっと以前、この「ブログ」を始めた頃、「カテゴリー」や「検索タグ」を決めろ、とか言うサーバーのうるさい要求に辟易して、たとえば「うつ病」とか言うタグをぶら下げているサイトを参照してみたことがある。
「今日は、少し楽だ、薬が効いたのかもしれない、・・・」みたいな独白が延々と続いているのを見て仰天して退散した。みずからの「私的」な事情を、延々と「語る」ことのみが「治癒」でありうることを否定しない。しかし「語る」には、少なくとも一人の「聞き手」が必要なので、彼、または、彼女を、「面白がらせ」なければ、そもそも聞いてもらえない。「うつ病」患者は、自分が、ほかならぬ「うつ病患者」のように見られることを極端に恐れる。すれ違えば不必要な大声でにこやかに挨拶をする。あの人、あんまりむずかしいこと考えてそうにないわね、と「切捨て」られることではじめて安心して「難しいこと」を考えることができるのである。
二項分布B(n,p)の、期待値。
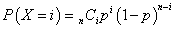
であるから、
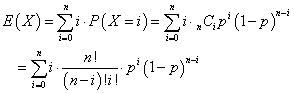
iとi!で約分したいのだが、
n!=n(n-1)!なる等式の成立する、nの定義域は、元来(笑)、n=2,3,4,・・・の筈である。!「階乗」は、ある自然数から次々に1を引いて掛け合わせ、1に至るもの、というのが「経験的」な定義であるべきところ、0!=1といわなければならなくなったのは、この式をn=1にも拡大して適用することで、「体系」の整合性を守ったからに他ならない、だから、ここでももちろん採用する。右辺のi=1に対応する項は、値が0であるから、Σ記号の基点を、こっそりi=1にすり替えても「実質的」には、差し支えない。でも、この「こっそり、すり替え」が私には、とても重要なことに思えるから。
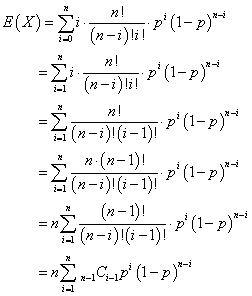
ここで、j=i-1なる「変数変換」を実施する。二項定理の「公式」を利用すべくこれに、「近づける」ことが動機である。
i=1→nに対して、j=0→n-1であるから、
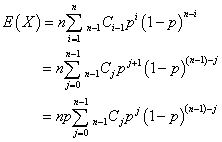
ここで、二項定理の式をn-1の場合に適用して、
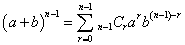
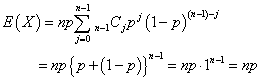
なるほど、B(100,0.5)では、E(X)=100・0.5=50、B(100,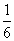 )では、E(X)=100・
)では、E(X)=100・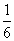 =16.666・・・、B(100,0.1)では、E(X)=100・0.1=10、なのである。
=16.666・・・、B(100,0.1)では、E(X)=100・0.1=10、なのである。
次、分散、および、標準偏差。
まず、準備。「分散」は、定義上、「偏差」すなわち平均値との差の2乗の平均値なのであるが、次のようにして、「2乗の平均」-「平均の2乗」と変形することができる。
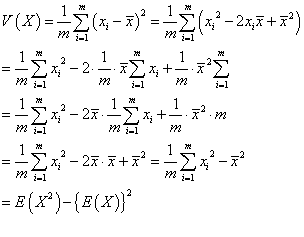
そこでまず、「2乗の平均」E(X2)を計算する。
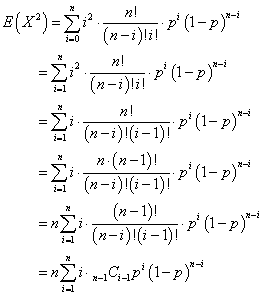
同様に、j=i-1なる「変数変換」を実施する。
i=1→nに対して、j=0→n-1であるから、
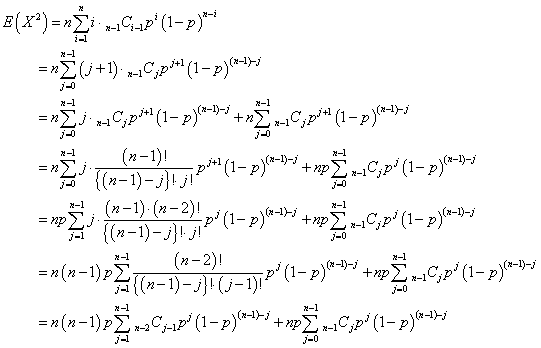
さらに、k=j-1なる「変数変換」を施して、
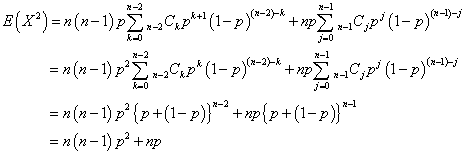
よって、
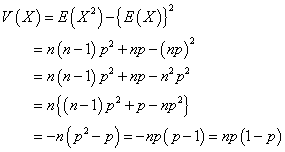
| 期待値E(X)=np | 分散V(X)=np(1-p) | 標準偏差σ=√V(X) |
| B(100,0.5) | 50 | 25 | 5 |
B(100,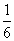 ) ) | 50/3=16.666・・・ | 125/9=13.888・・・ | 5√5/3≒3.727 |
| B(100,0.1) | 10 | 9 | 3 |
B(100,0.5)では、E(X)±σの範囲、すなわち、45と55の間に、
B(100,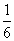 )では、12.94と20.40の間に、
)では、12.94と20.40の間に、
B(100,0.1)では、7と13の間に、
同じぐらいのデータが含まれているであろう、ことが「わかった」ので、ある。
それがどうした?、So_What?(笑)
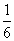 )
)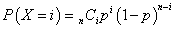
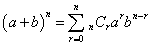
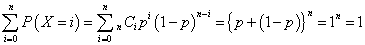

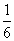 )、B(100,0.1)、のグラフを作ってみた。
)、B(100,0.1)、のグラフを作ってみた。
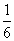 )、は、サイコロを100回投げて「6」が出る回数、と例えてよい。
)、は、サイコロを100回投げて「6」が出る回数、と例えてよい。
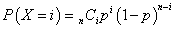
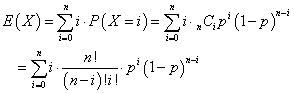
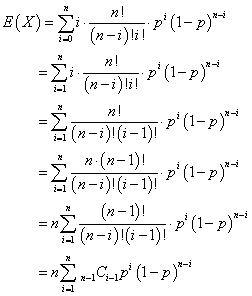
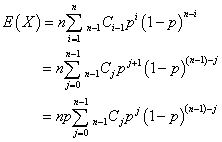
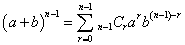
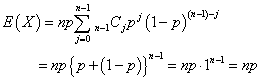
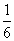 )では、E(X)=100・
)では、E(X)=100・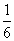 =16.666・・・、B(100,0.1)では、E(X)=100・0.1=10、なのである。
=16.666・・・、B(100,0.1)では、E(X)=100・0.1=10、なのである。
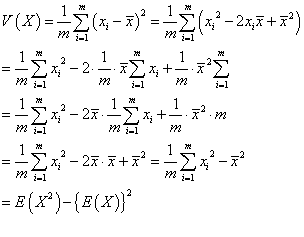
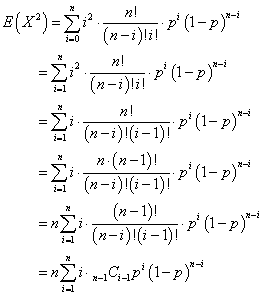
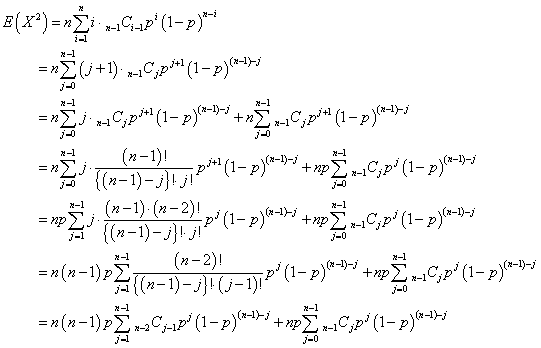
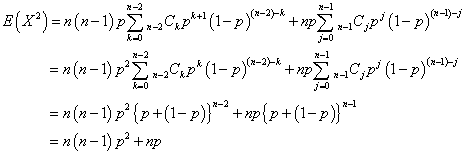
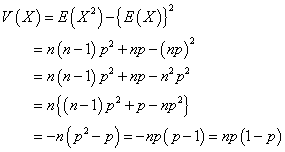
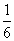 )
)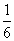 )では、12.94と20.40の間に、
)では、12.94と20.40の間に、