
[千葉大学2012_8]
- (1)「任意の」自然数nに対して、{an}が整数列ならば、2rは整数だということを示したい。(2)のように、「必要十分条件」は、とは問われていない。右向きの矢印だけ、証明できればそれで良いのである。
「任意の」自然数nに対して、{an}が整数列なんでしょ?、だったら、a1は整数だ、a2も整数だ、a3も整数だ、・・・、と列挙して、目的が達成された、つまり、2rが整数ならざるを得ないことが言えた、段階でやめればいい。- a1は整数であるから、a1=p+q+rは整数である。
- a2は整数であるから、a2=p+2q+4rは整数である。
従って、a2-a1も整数であるから、a2-a1=q+3rも整数である。 - a3は整数であるから、a3=p+3q+9rは整数である。
従って、a3-a2も整数であるから、a3-a2=q+5rも整数である。
従って、(a3-a2)-(a2-a1)も整数であるから、(a3-a2)-(a2-a1)=2rも整数である。
- (2)命題A⇔Bの形に書くと、
- A:{bn}が整数列である。
- B:p,q+r+s,2r,6sが、いずれも整数である。
それに対して、B→Aは、「任意の自然数に対して」、{bn}が整数列である、ことを示さなければならないから、具体的な自然数をいくつ並べても仕方なく、もっと「一般性」が要求される。こちらから始めよう。- B→Aを示す。
bn=p+nq+n2r+n3s
=p+n(q+r+s)+(n2-n)r+(n3-n)s
=p+n(q+r+s)+n(n-1)r+n(n-1)(n+1)s
ここで、n(n-1)は連続する二つの自然数の積であるから、いずれか一方が偶数であり、従ってその積も偶数である。従って、n(n-1)/2は整数である。
さらに、(n-1)n(n+1)は連続する三つの自然数の積であるから、少なくとも一個の3の倍数を含み、従ってその積は6の倍数である。従って、(n-1)n(n+1)/6は整数である。
よって、p,q+r+s,2r,6sが、いずれも整数であるならば、任意の自然数nに対してbnが整数であることは、以下の式から、明らかである。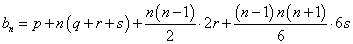
- A→Bを示す。
- b1は整数であるから、b1=p+q+r+sは整数である。・・・(ア)
- b2は整数であるから、b2=p+2q+4r+8sは整数である。
従って、b2-b1も整数であるから、b2-b1=q+3r+7sも整数である。・・・(イ) - b3は整数であるから、b3=p+3q+9r+27sは整数である。
従って、b3-b2も整数であるから、b3-b2=q+5r+19sも整数である。
従って、(b3-b2)-(b2-b1)も整数であるから、(b3-b2)-(b2-b1)=2r+12sも整数である。・・・(ウ) - b4は整数であるから、b4=p+4q+16r+64sは整数である。
従って、b4-b3も整数であるから、b4-b3=q+7r+37sも整数である。
従って、(b4-b3)-(b3-b2)も整数であるから、(b4-b3)-(b3-b2)=2r+18sも整数である。
従って、{(b4-b3)-(b3-b2)}-{(b3-b2)-(b2-b1)}も整数であるから、{(b4-b3)-(b3-b2)}-{(b3-b2)-(b2-b1)}=6sも整数である。
6s、2rが整数であることから、(イ)より、q+r+sは整数である。
q+r+sが整数であることから、(ア)より、pは整数である。
証明終わり。
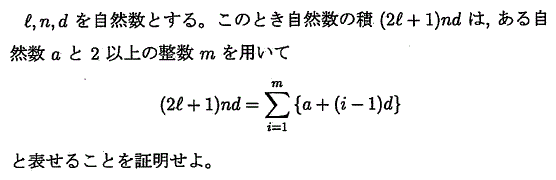
[千葉大学2012_12]
右辺は、初項a公差dの等差数列の初項から第m項までの和、を表しているね。
「表せることを」示せ、の解釈だが、
任意の自然数l,n,dに対して、上式を満たす自然数a及び、2以上の整数mの組が少なくとも一組、存在する、
ことの証明が要求されている、と読むことになる。後に明らかになるが、このような表現の仕方は、一通りとは限らない。そのすべてを列挙せよ、とは言ってない。ほら、ここに一つあるだろ、と言って、「逃げて」しまって、差し支えないのである。
右辺を変形すると、
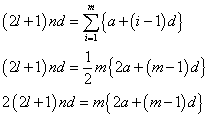
これは、与えられたl,n,dに対して、mに関しては2次の、aに関しては1次の「不定方程式」となっている。未知数が、m,a二つあるのに、条件式が一つしかないのだから、解が定まるわけはないのである。そこに、aは自然数である、とか、mは2以上の整数であるとか、様々な制限を付して、解が「有限個」に絞り込まれていくのである。これも後に明らかになるが、aは自然数でなくても、「半整数」、2倍したら整数になる数、であればよさそうで、また、どうしてmが、「自然数」でなく「2以上の整数」とされているか?、を慮って見るに、そりゃそうだ!、m=1なら、右辺はもはや、初項のみ、a=(2l+1)ndとすれば当然に成り立つから、「面白みがない」という判断なのだろう。
では、さしあたり、m=1も含むことにして、上式をmの2次方程式と見て、その自然数解について考察することにしよう。実は、1次方程式より、2次方程式の方が、「解の公式」だの「判別式」だの、「解と系数の関係」だの、道具が豊富なので扱いやすそうなのである。
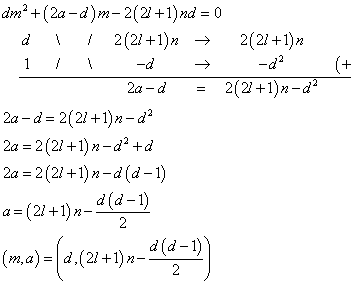
いわゆる「たすきがけ」というものの仕組みを考えて見るに、もちろんdには様々な因数がある場合もあろうが、仮に素数であったとしても、必ず、mの自然数解が存在しなければならないとしたら、2次の係数dは、d×1と分けざるを得ないし、定数項の2(2l+1)ndにも、たくさんの因数が存在するだろうが、少・な・く・と・も・、2、2l+1、n、dが約数であることは明白なのだから、それらについて検討して、確かに、自然数mに対して、aが、定まる!、と言えればいいのだろ?
上の例では、m=dなる解に対して、mが決まればaも決まる道理だから、aを算出してみた様子である。dとd-1は、隣接する整数だから、どちらか一方が必ず偶数、然らばd(d-1)/2は、整数である。
これで「ほぼ」出来ているのである。dが1でない限り、これが(m,a)の解のひと組である。だから、ほら、存在する、証明終わり、である。あとは、d=1のときの処方を考えればよい、それはそんなに困難ではなさそうだ。
と、自信たっぷりに書いたところで、完全に頓挫してしまった。dが1のとき、別の因数を発見するのが、どうやら、容易ならざるもののようなのである。
苦し紛れに、BASICで、以下のようなごく簡単なプログラムを書いて、l,n,dそれぞれ、1から5まで、条件を満たす2以上の整数m、および自然数aを列挙してみると、こんなとんでもないものになる。はじめ10まで列挙しようと思ったのだが、アプリケーションの表示の制限を超えてしまうみたいで、5までにしたのである。数が大きくなるにつれ、その約数の個数も増えるだろうから、当然ではある。
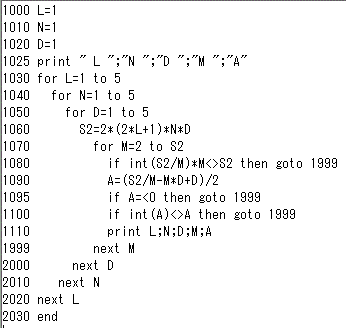

こんな数表を眺めて呆然としていても始まらないので、問題となるd=1の場合だけを抜き出したものをさらに下に掲げる。で、困ったことに(笑)「支離滅裂」なのである。「自然数は一つ一つ顔つきが違う」と、故・森毅が言っていたように、これこそが「整数論」の醍醐味なのであるが、例えば、l=4,n=5,d=1を見てみるに、mの候補は、3,5,6,9と四つある。その「意味」を問えば、5は、nそのものであり、9は、2l+1であるから、一般に(笑)2(2l+1)ndの約数であるが、3はなんだ?、(2l+1)の約数、これは、たまたま(2l+1)が9であったからだけのことであって、一般化できない、これが自然数「9」の、「顔つき」なんである。6はなんだ?、これも、2(2l+1)の一つの約数である、としか説明できない。
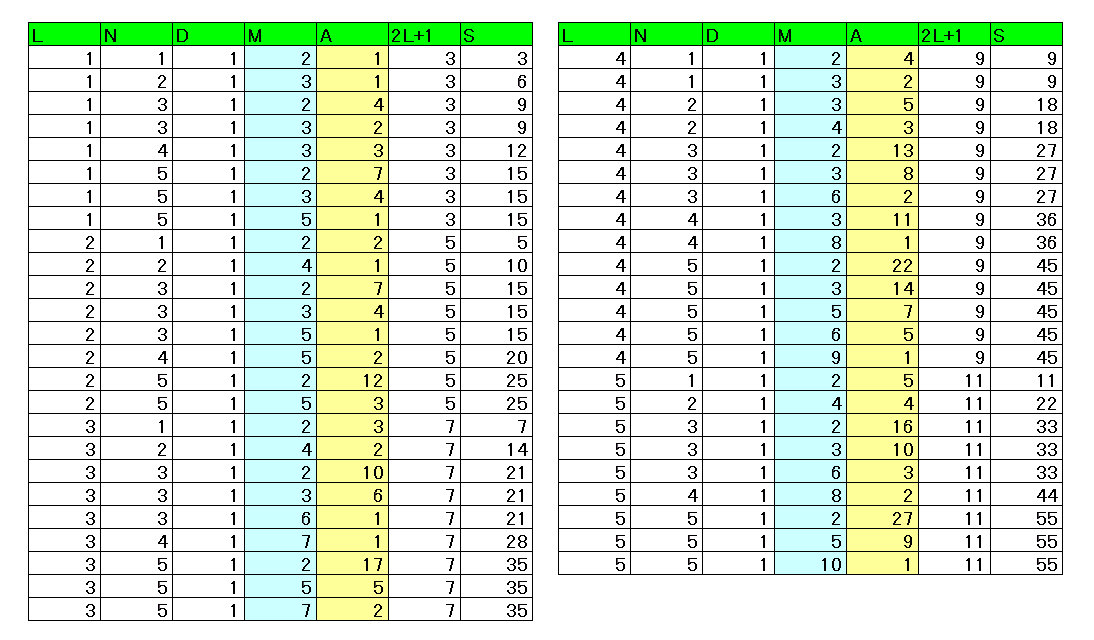
だから「頓挫」なのである。いかなる自然数l,n,dに対しても、ほら、これがmだ!、と言える物が見つからなければ「証明」にはならない。現時点で、dは「欠格」、なのである。
2(2l+1)ndには、数々の「1以外の約数」がありうるが、どんなl,n,dを選・ん・で・も・、必ずその約数だ!、と「胸を張って」言えるのは、
2、2l+1、n、d、2(2l+1)、2n、2d、(2l+1)n、(2l+1)d、nd、2(2l+1)n、2(2l+1)d、2nd、(2l+1)nd、2(2l+1)nd
4C1+4C2+4C3+4C4=4+6+4+1=15、大丈夫だ、ちゃんと15個ある。
これらすべてについて、mの候補としての、もっとも一般性を有する、ものを探さなければならない。
ところで、これ「入試問題」なんですよね?、一問20分そこそこで「解答」を出さなければならないはずの。私はすでに三日くらい考え込んでいる。ExcelやBASICといった「機械」の手も借りている。この時代に受験生でなかったこと、また、受験生に向かって、この問題が、ほら、こうして、私が示すように(笑)、スラスラと解くことができなければ、合格できない、などという真っ赤な嘘を、お義理でも述べ立てなければならない職業から「放逐」されてしまったことを(笑)、喜ばなければならない。
で、順次、これらの因数について逐一、検討することになる。それは、次回以降ご期待、ということで、本日は、これまで。
2(2l+1)ndの、少なくとも15個の因数について逐一、試してみよう。
- m=2とすると、
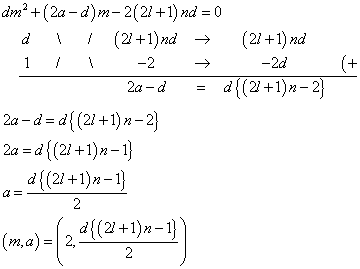
aが自然数であるためには、dが偶数であるか、または、nが奇数であることを要する。
別の言い方をすると、「dが奇数で、かつ、nが偶数のとき」、これは、解ではない。
(aが「半整数」でもよいのなら、もっと解がある、と先に述べたのはこの意味だ。) - m=2l+1とすると、
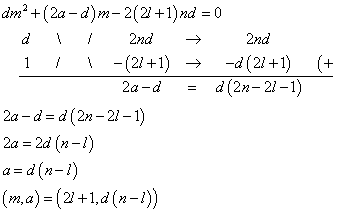
aが自然数であるためには、今度は、「n>l」という条件を付与しなければならない。
(aが0や負数も含む「整数」で良いなら、これも解である。) - m=nとすると、
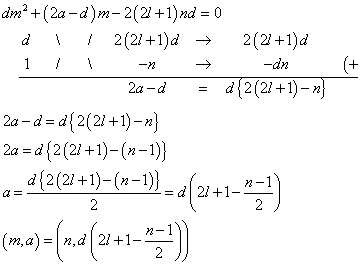
こちらには、n-1、dの少なくとも一方が偶数であること、つまり、nが奇数であるか、または、dが偶数であることを要する、という条件が付く。
別の言い方をすると、「dが奇数で、かつ、nが偶数のとき」、これは、解ではない。
また、mについての制限から、n=1のときも、使えない。
(aは「半整数」でよいなら、これも解である。) - m=dとすると、・・・、これは既に述べたが、もう一度掲げておく。
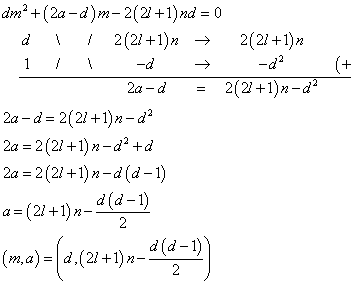
これは、既に述べたように、mについての制限から、d=1のときは、使えない、のみならず、
aが正であるためには、2(2l+1)n>d(d-1)などという複雑な不等式を、条件として盛り込まなければならなくなる。 - m=2(2l+1)とすると、
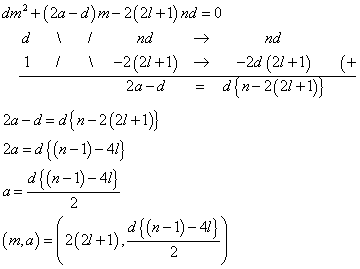
「d奇数、かつ、n偶数」でないこと、かつ、n>4l+1 - m=2nとすると、
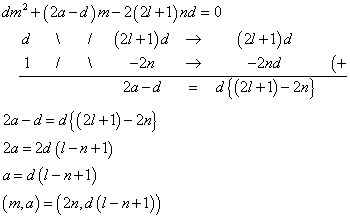
l>n-1であること、すなわち、lもnも自然数だから、l≧nであること。 - m=2dとすると、
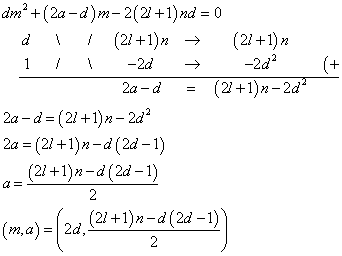
「nとdの偶奇が一致していること」かつ、(2l+1)n>d(2d-1) - m=(2l+1)nとすると、
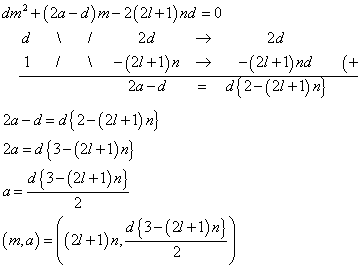
自然数l,nに対して、3>(2l+1)nということはありえないから、この式の適用場面は、ない。 - m=(2l+1)dとすると、
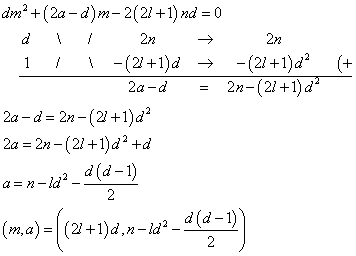
2n>2ld2+d(d-1) - m=ndとすると、

「dが偶数であるか、または、d,nがともに奇数であるか」かつ、2(2l+1)>d(nd-1) - m=2(2l+1)nとすると、
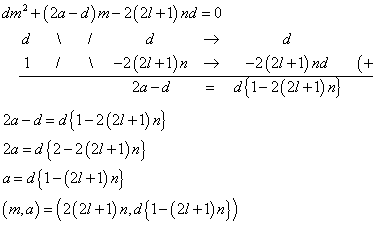
自然数l,nに対して、1>(2l+1)nということはありえないから、この式の適用場面も、ない。 - m=2(2l+1)dとすると、
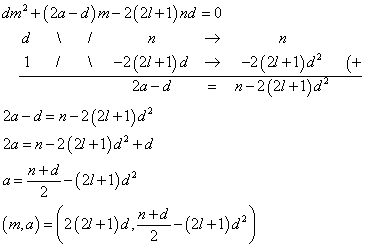
「nとdの偶奇が一致していること」かつ、n+d>2(2l+1)d2 - m=2ndとすると、
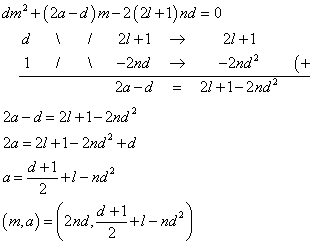
dが奇数であり、かつ、d+1+2l>2nd2 - m=(2l+1)ndとすると、
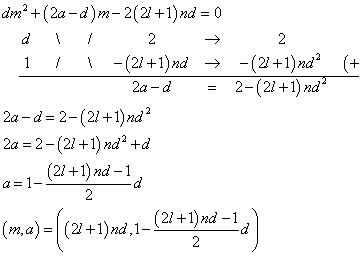
「dが偶数であるか、または、d,nともに奇数であるか」かつ、d+2>(2l+1)nd2 - m=2(2l+1)ndとすると、
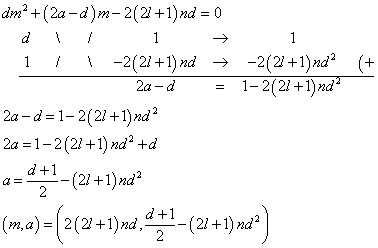
「dが奇数であること」かつ、d+1>2(2l+1)nd2
ということは、「付帯条件」がなるべくシンプルで、なおかつ、すべての場合をカバーしている、できれば二つの、解のセットを、得たいのである。早々に「うんざり」してしまったのは、かなりはじめの方で、それが発見できてしまったからだ。
- の要求する条件は、「n>l」
- の要求する条件は、「l≧n」
A∩B=φ、かつ、A∪B=U
ということだから、いかなる自然数、l,n,dのセットに対しても、「2」か、でなければ「6」の解が、存在する、と断言できるのである。
- n>lならば、
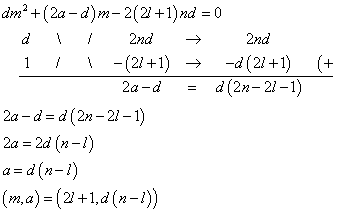
- l≧nならば、
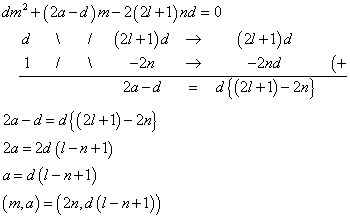
というわけだ。
こうして得られた解を、l,n,dそれぞれ1から5までについて、確かめてみた。
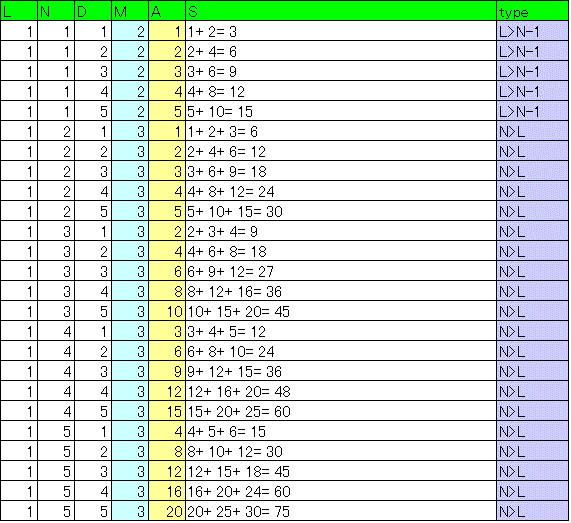
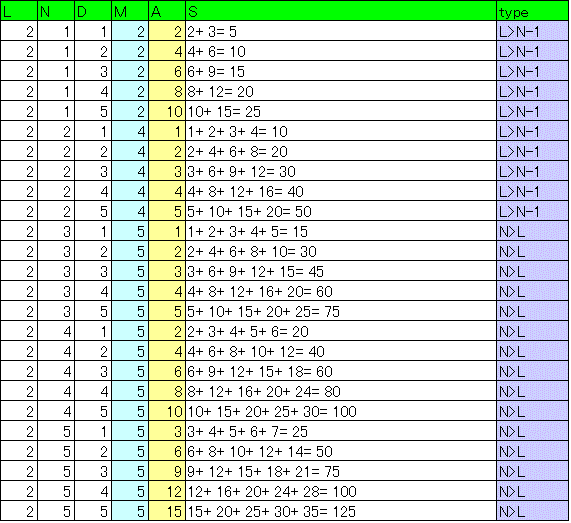
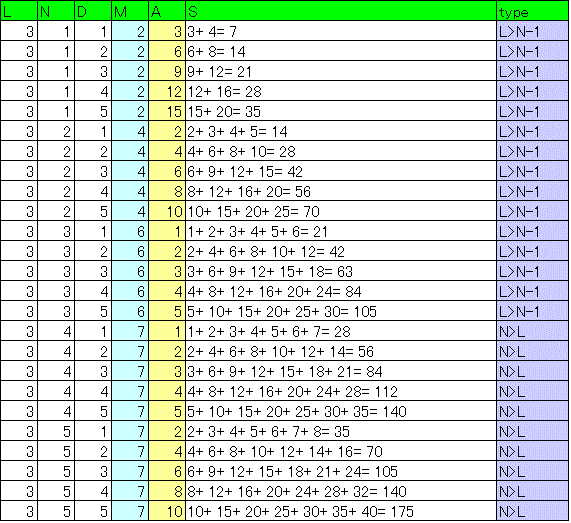
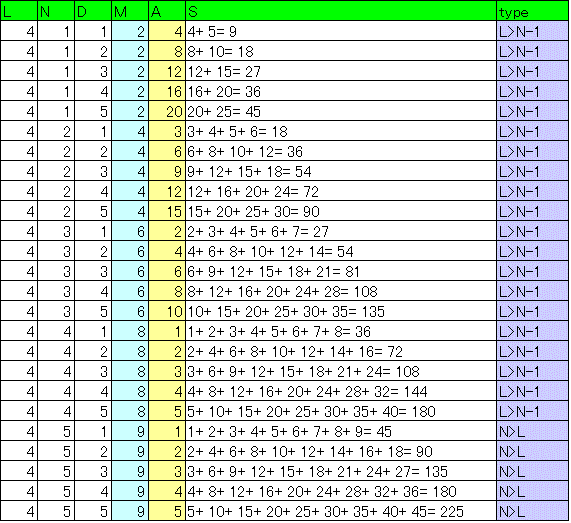
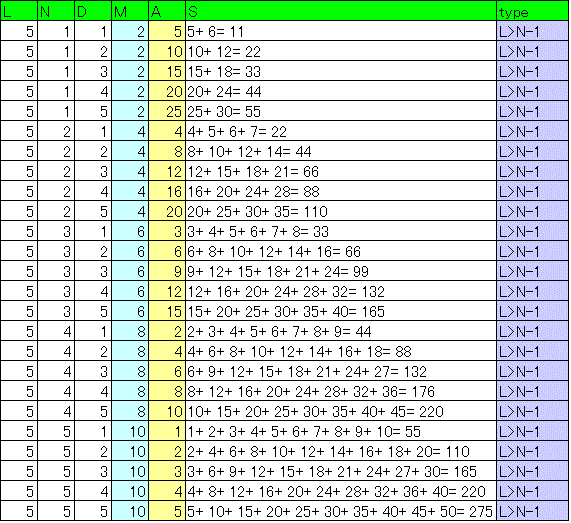


[千葉大学2014_13]
ここで言うf(n)なる数列、別の言い方をすると、
f(n)=[log2n]
右辺のかぎかっこのような記号は、「ガウス記号」、「・・・を超えない最大の整数」、つまり、「・・・以下の最大の整数」、を表す。
Excelのセル関数では、「=int(log(●●,2))」と書いて、●●に参照するセルの番地を書けば、下のようにいとも簡単に計算してくれる。
この数列は、群数列、元の数列を、ある規則に従って区分していく、その区分の「仕方」自体が一つの数列をなしている、数列の「上塗り」、「メタ・数列」みたいなもの、と見ることができる。
第2k項から、第2k+1-1項までは、ことごとくkという同じ数が並んでいて、この塊は、第k+1番目の「群」にあたる、というわけだ。
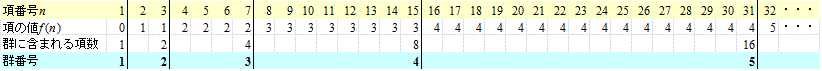
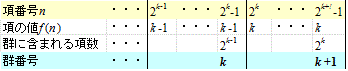
例えば「25」は、24≦25<25であるから、f(25)=4である。
(1)について、例えば「25」を例として、考えてみる。
自然数の逆数を並べた数列は、「調和数列」と呼ばれる。その謂れは、振動数の比が簡単な整数比であるほど、和音を作ったとき「調和性」が高い、と言われる。1:2なら「オクターブ」で同音名、2:3なら「完全5度」、ドとソの関係、3:4なら「完全4度」、ドとファの関係、というように。音速が同じ、例えば弦の材質と張り方が同じなら、振動数と波長は反比例するから、波長、例えば弦の長さは、その逆比になる、多分、そういう由来だと思う。
その「調和数列」の初項から第25項までを足す、という計算を想像してみる。とてつもない作業であろう。1から25までの自然数の分母を「通分」するのであるから。
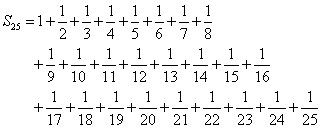
実際には、それらの数の中には、公約数が多々あるから、もっと小さくて済むのだが、強引に25!を公分母とした、としよう。下式のごとくになるはずだ。かっこの中の各項は、分数のように見えるが、もちろん、25!を、1から25のどれかの数で割り算しているのだから、割り切れて整数になっている。この和が、分子となるのである。問題は、分母の25!との間にどれほどの公約数があり、どこまで約分できるか?、なのだ。ここでは、偶数・奇数、つまり2という約数を含むかどうかが問題とされている。
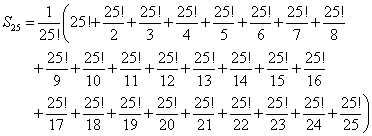
そこで、こんなことを考える。1から25にいたる自然数のうちには、偶数が多々あり、4の倍数も、8の倍数も、16の倍数さえあるから、25!には、2という因数がたくさん含まれている。それを計算することも可能であろうが、計算できたとして、それは必ず、25という数からある手続きを経て得られるものであるから、一般にn!を素因数分解したときの2の指数を、g(n)と表記することにして、g(25)としよう。
そうして2という因数をひとまとめにしてしまえば、ほかの因数は、唯一の偶数の素数は2であるから、すべて奇数、奇数と奇数を何回かけてもことごとく奇数だから、これも一般に、n!を素因数分解したときの2以外の因数を全部かけたものをbnと呼ぶことにすれば、25!は、
25!=2g(25)・b25
と表すことができる。ここで定義したbnなる「奇数」は、問題文のものと同じになることが、のちに分かる。
さて、下は、25!を、すべて2g(25)・b25にすりかえたところ。分母にも、ところどころ2を因数にもつものが現れるから、のちに約分するために、分けて表記した。
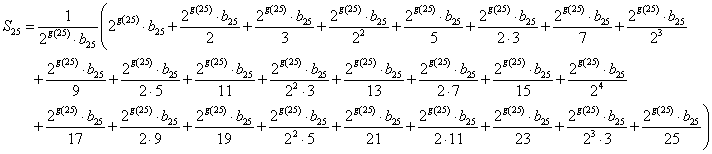
ここで、問題文に定義されているf(n)なる数列(関数)が登場することになる。
24≦25<25であるから、f(25)=4である、ということを思い出せば、かっこの中の25項のうち、24を因数にもつものが、「16」た・だ・一・つ・存在し、その他はすべて、たかだか、23までしか因数に含まない。
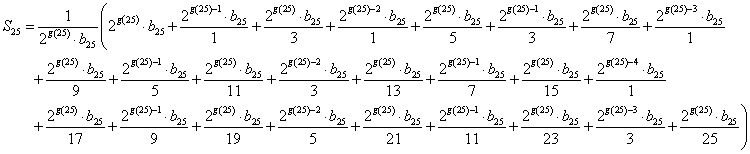
約分を実行した。かっこ内の各項は、分数の形をしているからややこしいけれども、分母からは2という因数が全部排除され、残っている奇数は、もちろんことごとく25より小さいものだから、これは当然b25なる奇数との間で約分されるはずだから、すべて整数である。
それらの、「共通因数」を、かっこの前に出したいのだが、2を因数とするものについてのみ考えるとして、かっこ内の各項で2の次数が最も「低い」のは、分母が24という最も「高い」次数だった第16項である。だから、2g(25)-4を「共通因数」として、かっこの前に出すことができる。
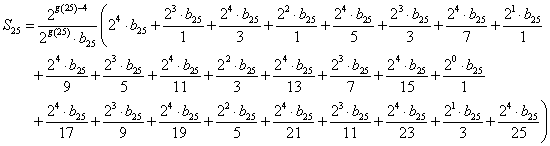
さてかっこ内の各項を眺めると、くりかえすが、分母の奇数はb25との間で約分されているから、すべて整数である。
第16項のみが、2という因数をもっていない。他の項はすべて、2という因数が、残っている。だから、かっこ内は、奇数なのである!、これを改めて、a25と名付ける。
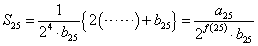
というわけだ。「25」を一般化して「n」とし、若干の表現を変えれば、これで証明になる。
(2)は問題ないだろう。n≧2に対して、f(n)≧1、ならば、(1)で示されたSnの分母は偶数であり、分子anは奇数であるから、Snが整数になることはない。
その調子で、(2)を利用して、(3)もあっさり片付くかと思いきや、頓挫した。
Sm,nは、
Sm,n=Sn-Sm-1
と表すことができる。
(2)の結果から、Snも、Sm-1も、整数ではない、これ以上約分できない分数、既約分数になっている。その差もまた整数だと言いたければ、通分した際の分子・分母が、互に素であることを言えばよい。
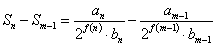
ここで、自然数m,nは、m<nであるから、nとm-1との間には少なくとも2の差がある。
上の表を参照すればわかるように、
- f(n)>f(m-1)、である場合と、
- f(n)=f(m-1)、である場合と、
- f(n)>f(m-1)、である場合
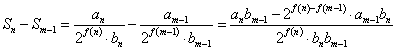
右辺の分子の第1項は奇数、第2項は偶数、従って分子は奇数、これに対して分母は偶数であるから、これは整数にはならない。 - f(n)=f(m-1)、である場合
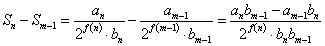
となり、分子は、奇数引く奇数だから偶数になってしまい、少なくとも2で約分できてしまう。約分できた後もなお分子分母が互に素だと言うためには、何か別の論理が必要なようである。
例えば、n=7,m=5にしてみよう。f(7)=f(5-1)=2である。
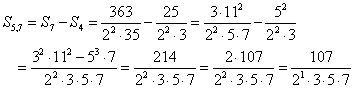
こんなの、筆算や電卓でやったんじゃない。二十代の初めに3年足らず働いただけなのに(笑)、「三つ子の魂」とでも言おうか、「元・プログラマ」の性癖は抜けないようで、計算が面倒と思ったときは、プログラムに頼ろう!と思ってしまう。結果としては、往々にしてその方が時間がかかるのだけれど、プログラミングというものには、何か「魔力」があって、まことにしばし「取り憑かれ」て、しまうのである。せっかくだから、紹介する。(1)で説明したロジックに従って、いったんn!を計算した上で、2という素因数だけを洗い出し、とりあえず「奇数」としてのan,bnを計算する。でも、両者には、2以外の共通因数がいくらもあるだろう、それを探して逐一約分する、などという「無駄」な方法を採用しているから、数字が大きくなると、演算時間が滅法、長くなる。せっかくだから、n=1〜25まで計算させたいんだけど、今現在、24のところで止まっている。あとしばらく待って、答えがでないなら、「強制終了」させることになる(笑)。これも「情報理論」の、アポリアの一つで、シンプルなプログラムで済ませようとすると、演算時間が長くなり、演算時間を短縮させようとすると、プログラムが長くなる、ものなのである。

n=1〜24までの結果。an,f(n),bnを計算した。
S( 1)= 1/(2^ 0* 1)
S( 2)= 3/(2^ 1* 1)
S( 3)= 11/(2^ 1* 3)
S( 4)= 25/(2^ 2* 3)
S( 5)= 137/(2^ 2* 15)
S( 6)= 49/(2^ 2* 5)
S( 7)= 363/(2^ 2* 35)
S( 8)= 761/(2^ 3* 35)
S( 9)= 7129/(2^ 3* 315)
S( 10)= 7381/(2^ 3* 315)
S( 11)= 83711/(2^ 3* 3465)
S( 12)= 86021/(2^ 3* 3465)
S( 13)= 1145993/(2^ 3* 45045)
S( 14)= 1171733/(2^ 3* 45045)
S( 15)= 1195757/(2^ 3* 45045)
S( 16)= 2436559/(2^ 4* 45045)
S( 17)= 42142223/(2^ 4* 765765)
S( 18)= 14274301/(2^ 4* 255255)
S( 19)= 275295799/(2^ 4* 4849845)
S( 20)= 55835135/(2^ 4* 969969)
S( 21)= 18858053/(2^ 4* 323323)
S( 22)= 19093197/(2^ 4* 323323)
S( 23)= 444316699/(2^ 4* 7436429)
S( 24)= 1347822955/(2^ 4* 22309287)
S( 25)= 3.22560603614268731E19/(2^ 4* 528308665525265625)
あ、今返ってきた。なるほど、桁あふれして指数表記になっている。下19桁は「概数」だから、これでは「整数問題」は扱えない。
で、これを利用して、上の計算をしてみたわけだが、なるほど、分母の素因数2の指数f(n)とf(m-1)が同じであるときは、分子は奇数引く奇数で偶数となるから、分子は2という因数をもつ、そこで約分が行われるのだが、どうやら、分母の2の指数の方が必ず大きい、ということを言わねばならないらしいが、この数字からは、何も見えない。というわけで、頓挫、である。
頓挫したときは、一歩後退してみるしかない。一応、目算はついたのだが、本日は、これまで。
今日の、数学の入試問題は、(1),(2),(3)といった具合に、「小問」形式に分割されていることが多いのだが、・・・、「今日の」と言ったのは、もちろん、「昔は」(笑)そうではなかった、「〜を証明せよ」みたいな一行きりのものが多かった。「親切」になってきた、わけだが、これはもっぱら採点者側の便宜によるものだろう。証明の方針をほのめかすことで、いわば「突飛な」、ひょっとしたら採点者も理解できないような「天才的な」答案が出現するのを、防止したいのである。そうして、採点者個人の嗜好に左右されかねない恣意性を排除したいのである。
それ自体は悪いことではないだろう。「話の流れ」や「空気」(笑)を「読む」ことが得意な、「適応度の高い」個体が選ばれ、選ばれなかった者は、「そうか、私はやっぱり、天才だったからだ」と不幸を託っていればよいのである、などと皮肉なことを言いたいのではなく、・・・、やはり凡人にとって、数学的認識の深化というのは、具体例から一般的定式化、より単純な場合の定式を、より複雑な 場合にやや変容して応用する、などというプロセスをたどるのが「普通」だからだ。
だから、せっかくの出題者の示してくれた誘導の「意図」を、「読まなければ」ならないのだが、もちろん、人は往々にして、「読み違える」。
私は、(1)と(2)から導かれた「結論」を用・い・て・、(3)が導かれるんだ!、と即断し、その思い込みに従って、
Sm,n=Sn-Sm
と「飛びついた」のだが、頓挫した。
そうではなく、(1)と同じように、(1)を真・似・て・やれ、というのが「誘導」の「意図」だったかもしれない。
(1)でやったのと同じように、各項の分母を全部かけ算したものを公分母として通分してみる。
まずは、下の二つの例示。いずれも4項のものを取り出してみた。いずれも、最後の行で、ちゃんと、「分母が偶数、分子が奇数、だから、整数ではない」という論証にはなっている。
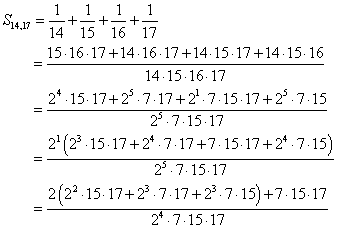

分母は連続4自然数の積、分子の各項は、その4数の積から、ひとつずつ、除外した積になっている。分子と分母から、2という素因数について、くり返しできる限り最・後・ま・で・、約分していった結果、分子は奇数になったが、分母にはまだ2が残っている!、ということを言いたいのである。分子の各項の共通因数に含まれる素因数2の「冪(ベキ)」、右肩に付く指数のことだ、が、分母の、同じく2の「ベキ」より、小さい、ということが言いたい。共通因数2をことごとく取り除いたかっこの中身は、当然奇数であるのだが、証明が都合よく行ってもらうためには、「他の項はすべて偶数なのに、た・だ・一・つ・だ・け・奇数の項がある」と言えれば、とてもありがたい。ということは、・・・、
mからnまで、連続した自然数を適当に選べ。
どんな選び方をしても、その中には、素因数2の「ベキ」が、最も高いものが、た・だ・一・つ・、含まれる。
ということを証明することに帰着する。ここまで言ってもまだわからない「頭の悪い」諸君(笑)、つまり、私のことだが、のために、例を挙げた。
上のはじめの例、(14,15,16,17)では、16=24、
次の例、(10,11,12,13)では、12=22・3、
がそれぞれ2の「ベキ」が最高である。通分していった時に、分子のこの数に対応する項の2の「ベキ」は、反対に最も小さくなる。その数だ・け・が、含まれないのだから。最後まで約分した時、奇数になるのは、この項である。そんな項がいくつも、とりわけ、偶数個、存在してもらっては、困る!、できれば、必ず、一個であってほしい。
改めて、f(n)の表を眺めてみよう。
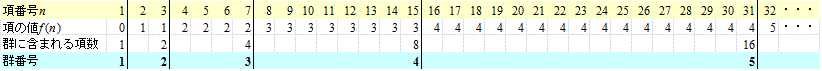

二つの自然数m,n、ただしm<n、を選ぶ。「頭の悪い」私のために(笑)、あくまで例え話を続けるが、
- この数列のいくつもの「群」にまたがる二数を選んだ場合、例えば、(m,n)=(6,20)、この中で2の「ベキ」が最も高いのは、16、それは、最高数n=20に対応するf(20)=4、だから、2f(20)=16、が、「選ばれた」のである。一つの「群」、第n群には、2f(n)なる項は、当該「群」の左端に、ただ1項しか、存在しない。
- もう少し微妙な議論が必要になりそうなのは、同一の「群」から二数を選んだ場合、
例えば、(m,n)=(18,27)、なら、24=23・3だろう。f(27)=4、だから、この「群」には24という項が一つしかないのは当然、23を因数に含む項も24ただひとつしかないのである。なぜか?、それはね!、2が、二番目の自然数、だからだ。
2kと、2k+1との間には、すなわち、2・2k-1と、4・2k-1との間には、3・2k-1しか存在できない。なぜなら、自然数2と自然数4の間には、自然数は3しかないからだ!
では24すら含んでいなかったらどうなるのだ?、例えば、(m,n)=(18,23)、なら?、今度は、20=22・5が、やはり、唯一つ、選ばれる。f(n)=4であるグループ、第5群を24を境に二分割し、前半の「サブ・群」について、同じ論理を適用すればよい。
上に、二つの例を挙げたのは、これらの少し扱いの異なる二つの場合に対応している。
(14,15,16,17)は、第4群と第5群にまたがった選び方、
(10,11,12,13)は、第4群の中で二数を選んだ場合。
これに、少々(笑)「一般化」の体裁を施せば、証明になる。本日はここまで。といっても、「解決」が見えてしまうと、急速に興味を失うのが人の常、ちゃんと「一般化」してみるかどうかは、不明(笑)。
ここまでやってみて初めて気づくのだが、むしろ(3)が「一般」で、(3)を先に証明することができれば、(1)は、m=1のとき、というその特別なケース、に過ぎなくなるのである。
さすれば、(1)から(3)の流れは、「具体から抽象」、「個別から一般」、への流れだったことになる。

[千葉大学2013_6]
- (1)
n=0,1,2,3,・・・、k=0,1,2,3,・・・に対して、
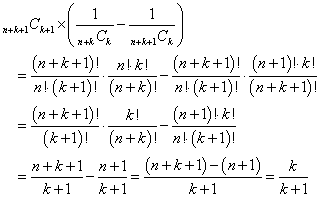
なるほど、nによらない値である。 - (2)上で得られた式を、ちょいと変形すると、
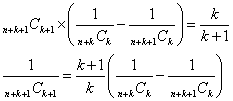
和が求められている数列の各項が、この式の左辺に当たるのだ、と思えば、k+1=3は常に一定である。ならば、(k+1)/k=3/2で一定、右辺は、kは同じままで、n番目から、n+1番目を引く、という形をしているから、うまくすれば、隣接項のプラスとマイナスが、全部キャンセルされるのでは?、という期待が持てる。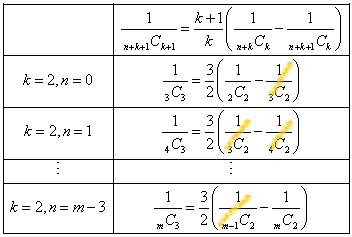
「期待通り」だったわけで、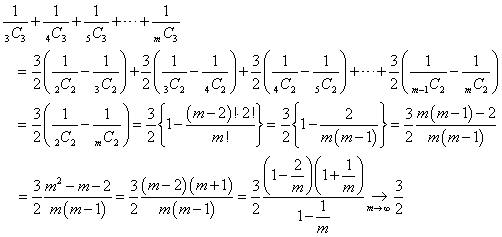
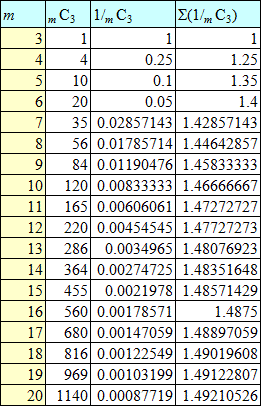
と、なったわけだが、一体、この式が、何を「意味」しているのかは、とんとわかりませぬ。
自然数m,nに対する「ベータ関数」、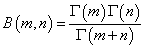
自然数nに対する「ガンマ関数」、
Γ(n)=(n-1)!
と、何か関係がありそうではあるが、今のところ、不明。
いろいろ考えてみたが、ベータ関数、ガンマ関数との関係は不明のままだが、というか、多分、そんなに関係なさそうな気もしてきたが、それとは別に、この式をの和を求めるのに、もう少し「直接的」な方法を思いついた。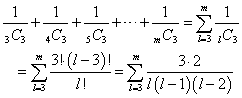
となる。分母が3次式、これを二つの2次式の「部分分数」に展開する、というのは、ありそうな方法だが、l,(l-1),(l-2)という3数が、「非対称」であることが、困・っ・た・ことなのである。そこで、「変数変換」j=l-1を施すと、なんと!、綺麗に隣接項同士が、キャンセルされる。1ずらすだけで、「対称性」が、回復されるのである、大袈裟に言うのならば。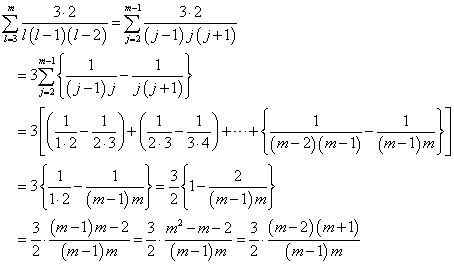

[千葉大学2014_5]
- (1)
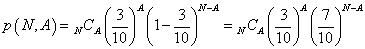
- (2)
- (i)
- b≧aのとき
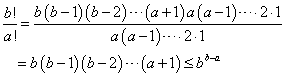
- b<aのとき
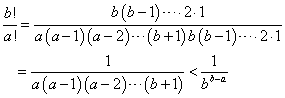
- b≧aのとき
- (ii)
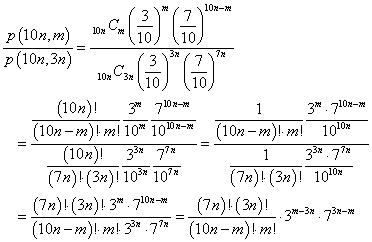
ここで、(i)より、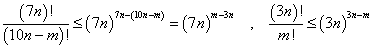
であるから、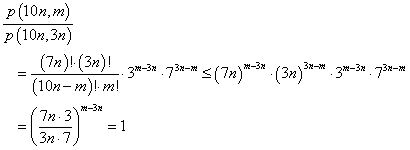
p(10n,m)≦p(10n,3n)
であるから、p(10n,m)ただし、m=1,2,3,・・・,10n、のうち、最も大きいのは、p(10n,3n)であることが示された。 - (i)
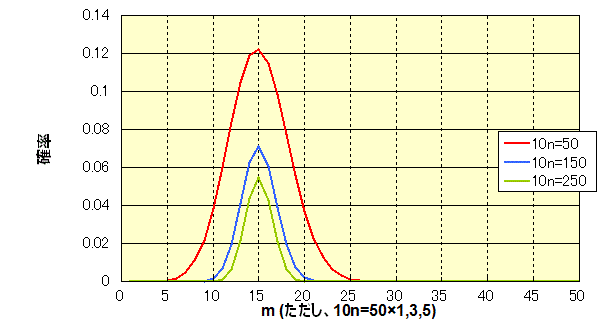
これは、二項分布B(10n,0.3)なのだから、その平均値m=10n×0.3、n=5なら、m=15、n=15なら、m=30、n=25なら、m=45、で、それぞれ「ピーク」になるのは、当然、といえば当然、だったのであるが。