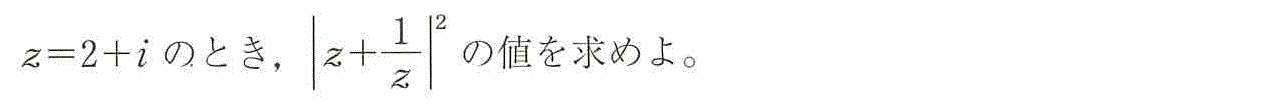


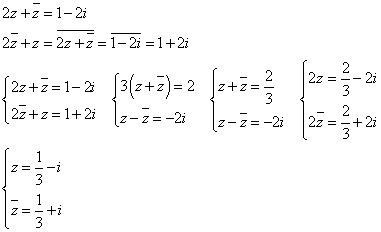

(1)
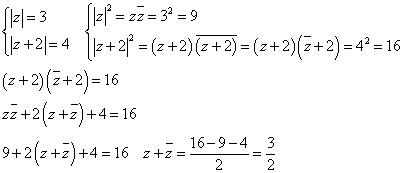
(2)
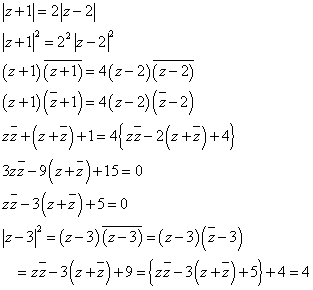

|
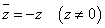 を示したい。
を示したい。
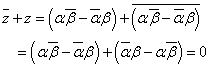
ここで、もし、z=0ならば、
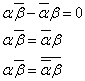
となり、
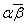 は実数であり、仮定に反する。
は実数であり、仮定に反する。
よって、z≠0(背理法)
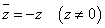 であるから、zは純虚数である。
であるから、zは純虚数である。
(2)
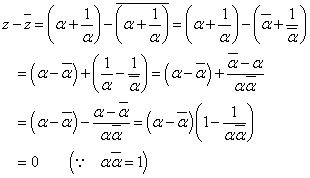
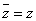 であるから、zは実数である。
であるから、zは実数である。

α≠0である複素数α、βに対して、以下のことを証明する。
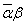 が実数であるならば、β=kαとなる実数kが存在する
が実数であるならば、β=kαとなる実数kが存在する
- β=kαとなる実数kが存在するならば、
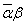 は実数である
は実数である
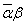 が実数であるから、
が実数であるから、
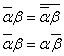
α≠0だから、 したがって、
したがって、
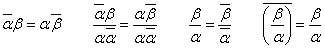
であるから、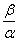 は実数である。
は実数である。
よって、β=kαとなる実数kが存在することが示された。- β=kαとなる実数kが存在するならば、

となり、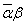 が実数であることが示された。
が実数であることが示された。

(1)
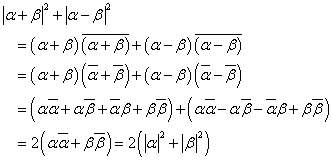
(2)
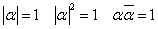
であり、ここから、
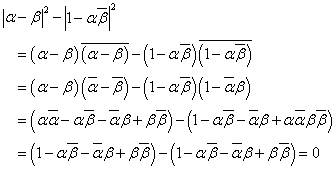
一方、

であるから、
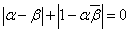 のとき
のとき
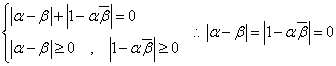
であるから、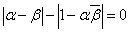
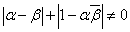 のとき
のとき
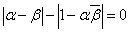
よって、いずれの場合も、示された。
(3)
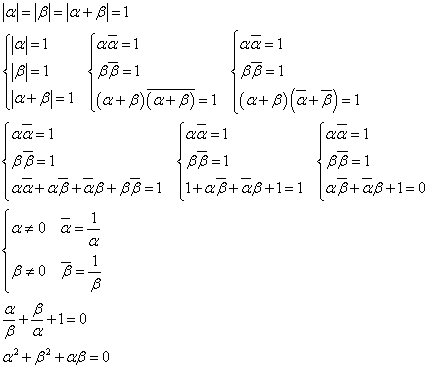
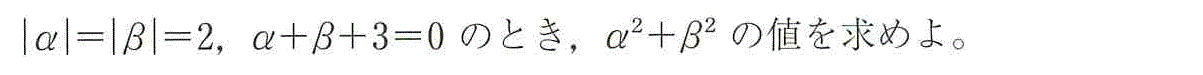
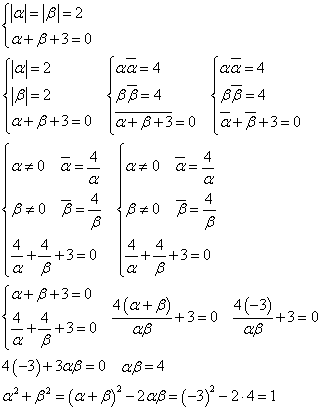

(1)
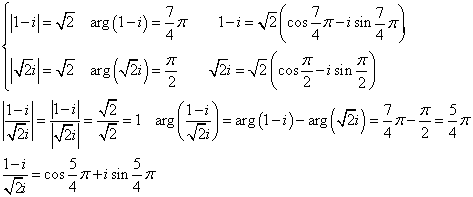
(2)
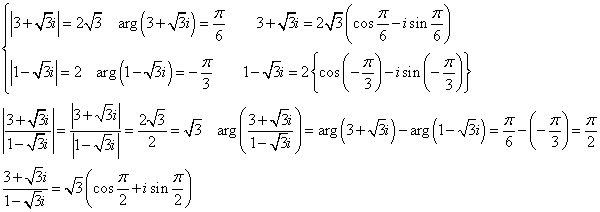
(3)

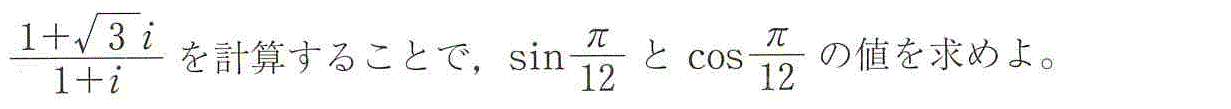
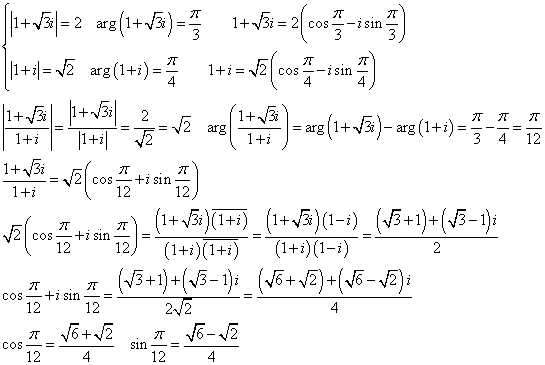


(1)
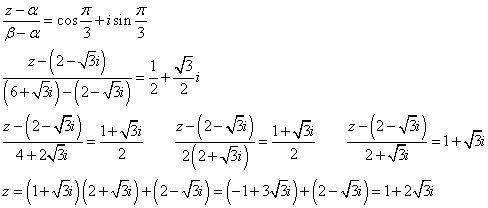
(2)
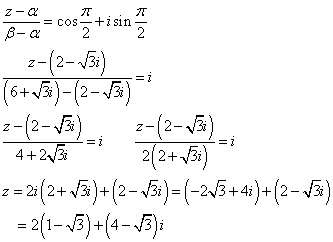
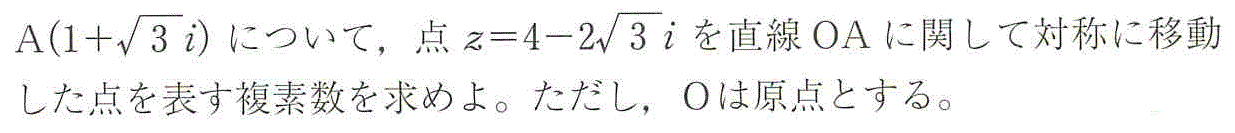

α=1+√3iに対して、A(α)、P(z)、また、求める点を、Q(z')、と定めると、
∠AOP=θに対して、∠AOQ=θであるから、
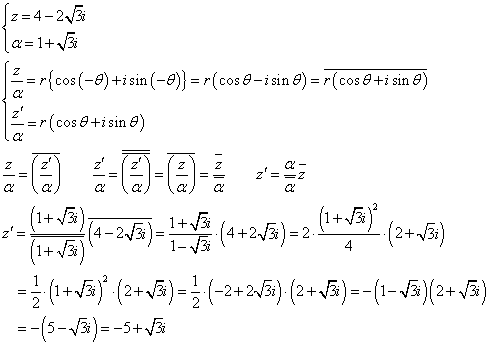
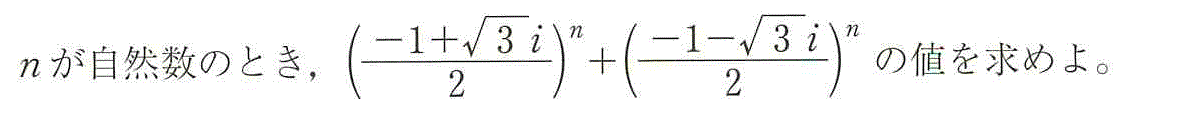
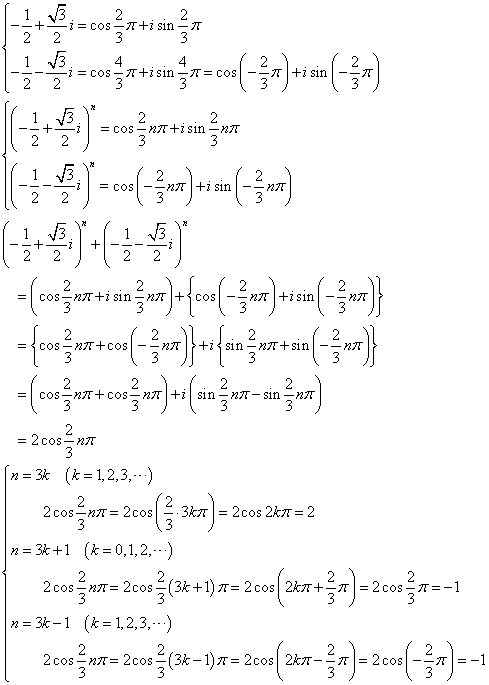

(1)
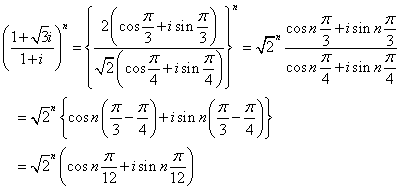
虚部が0となる最小の自然数nは、

(2)
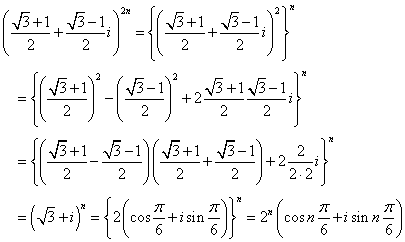
虚部が0となる最小の自然数nは、
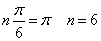
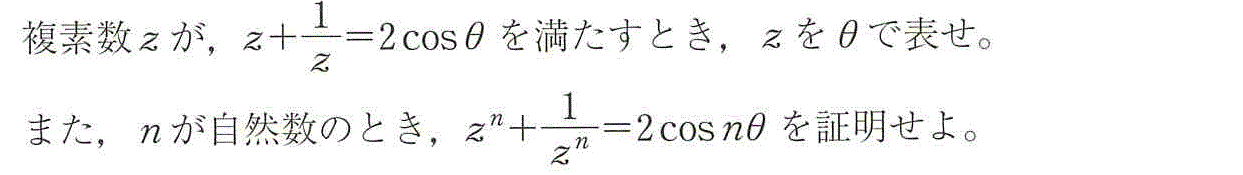
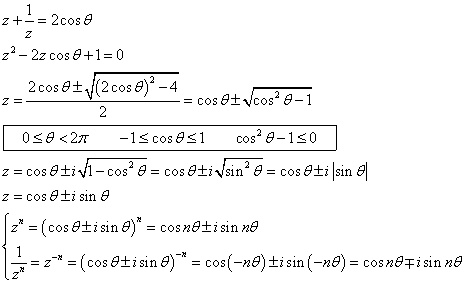
ただし、「複号同順」である。
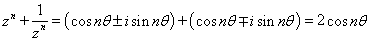
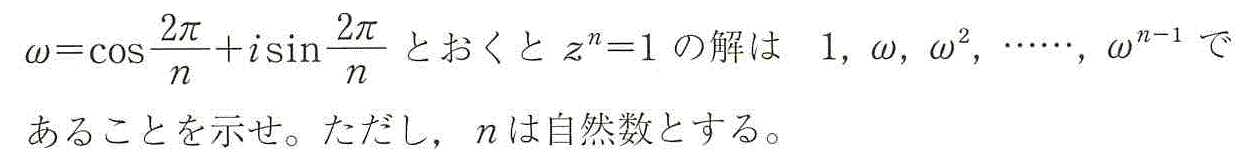
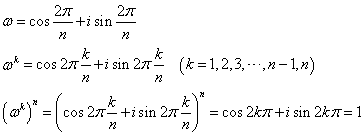
よって、k=1,2,3,・・・,nに対して、ωkは、zn=1の解である。
ただし、k=nのとき、ωn=1であるから、すべての解を列挙すると、
z=1,ω,ω2,・・・,ωn-1

(1)
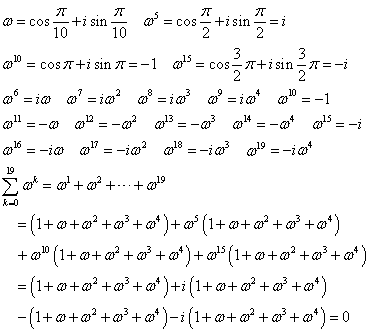
[別解]
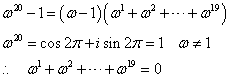
(2)
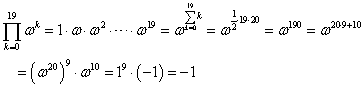
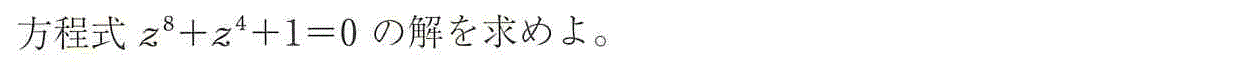
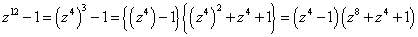
であるから、z8+z4+1=0の解は、
z12-1=0の12個の解のうち、z4-1=0の4個の解、以外のもの、
ということになる。
z12-1=0の12個の解は、
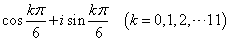
z4-1=0の4個の解は、
z=1,-1,i,-i
であり、これらは、上の12個の解のうち、それぞれ、k=0,6,3,9の場合にあたる。
よって、求める解は、
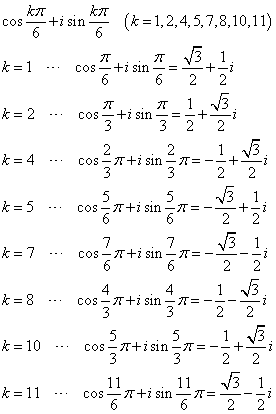
[別解]
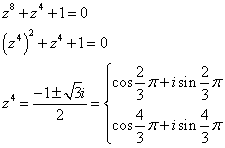
ここで、|z|=1であるから、argz=θとおけば、
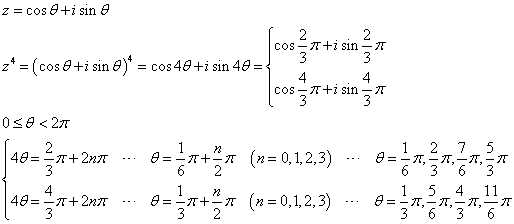
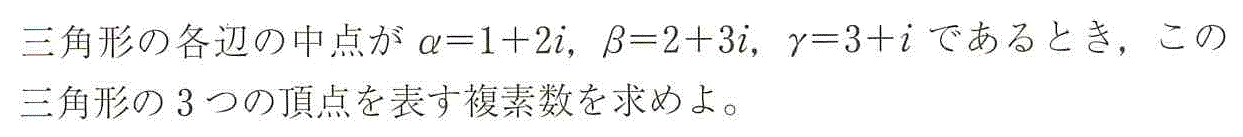
求める三頂点をそれぞれ、z1,z2,z3とすると、
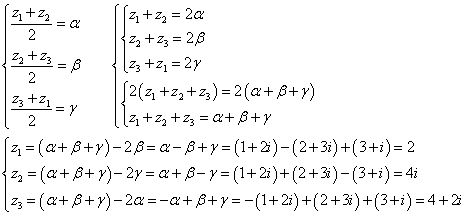

求める三頂点をそれぞれ、α、β、γとすると、
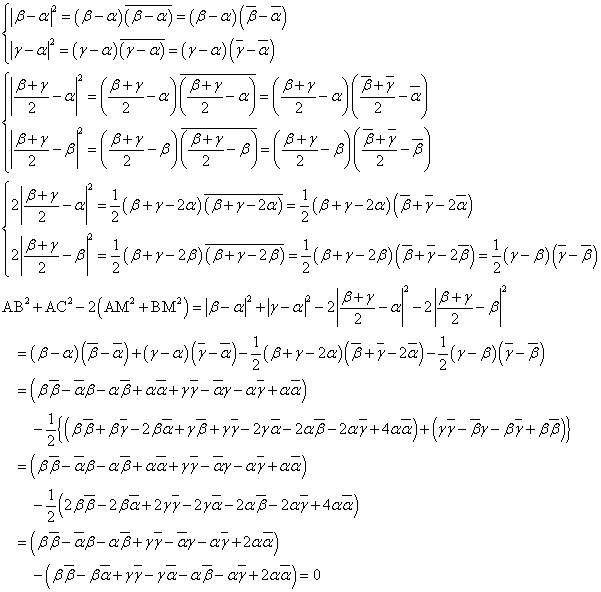
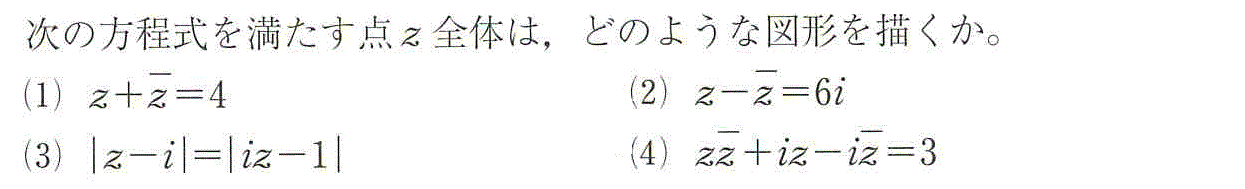
(1)
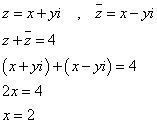
点A(2)を通り、実軸に垂直な直線。
(2)
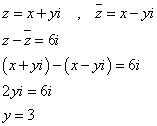
点A(3i)を通り、虚軸に垂直な直線。
(3)
点A(i)、点B(-i)を結ぶ線分の垂直二等分線、すなわち、実軸。
(4)
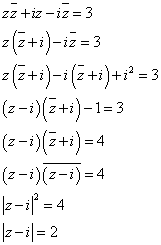
中心A(i)、半径2の円。
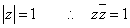 であるから、
であるから、
(1)
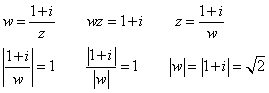
原点中心、半径√2の円。
(2)
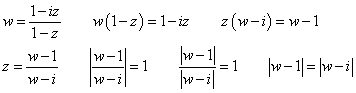
点A(1)、点B(i)を結ぶ線分の垂直二等分線、すなわち、直線y=x
(3)
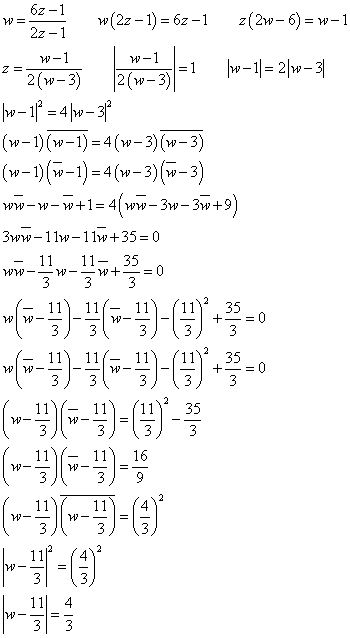
中心A(11/3)、半径4/3の円。
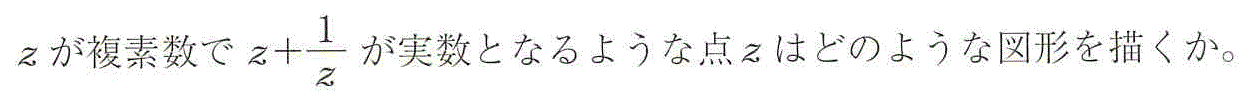
条件より、
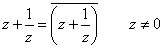
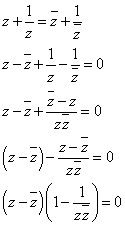
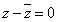 のとき、zは実数、ただしz≠0
のとき、zは実数、ただしz≠0
すなわち、実軸、ただし、原点除く。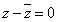
原点中心、半径1の円。
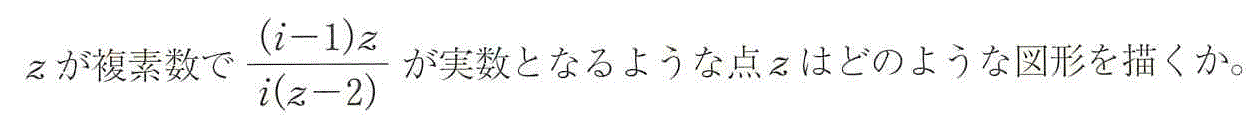
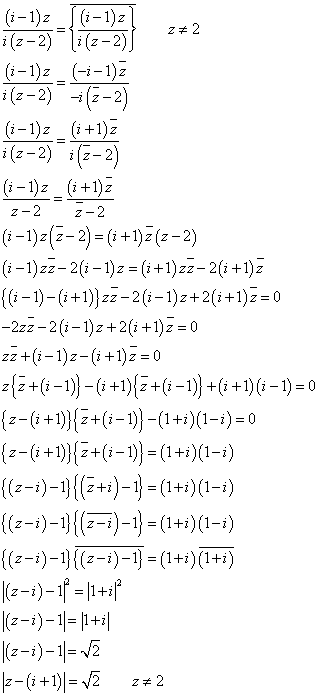
中心A(1+i)、半径√2の円、ただし、点B(2)を除く。
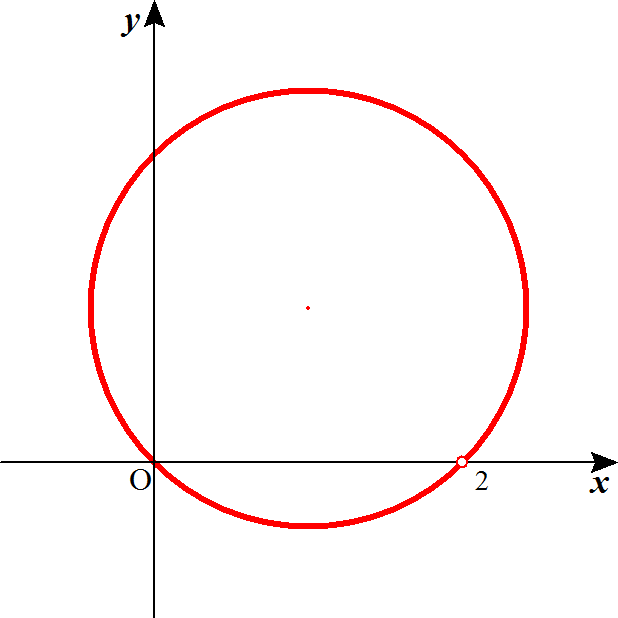
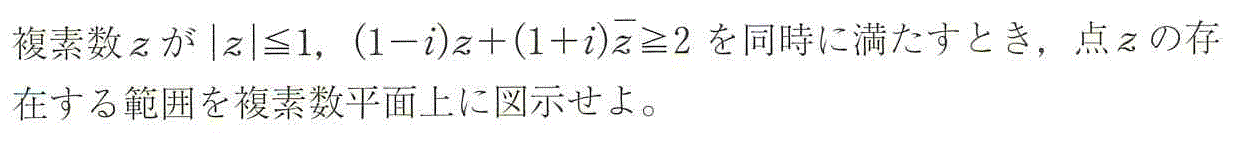
|z|≦1・・・(1)
これは、原点中心、半径1の円の内部および周を表す。
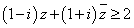 ・・・(2)
・・・(2)
z=x+yiとおくと、
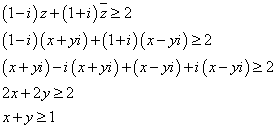
(1)(2)より、
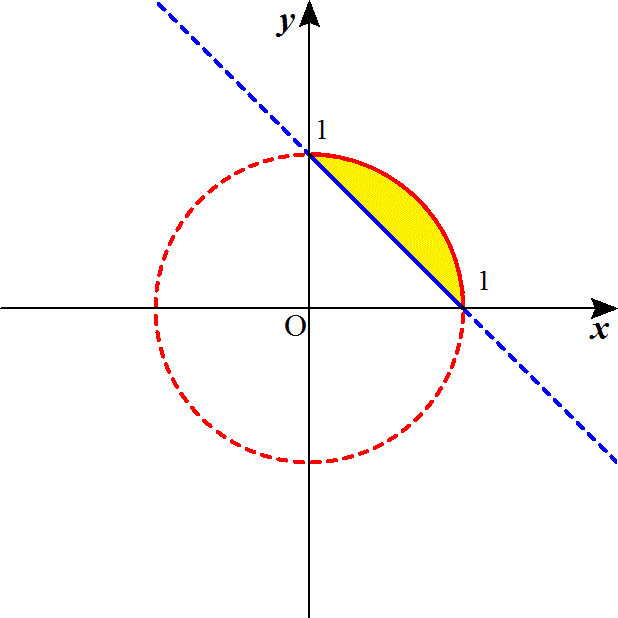

(1)
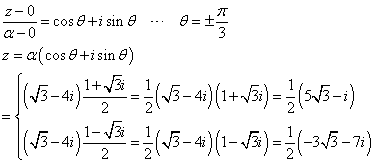
(2)
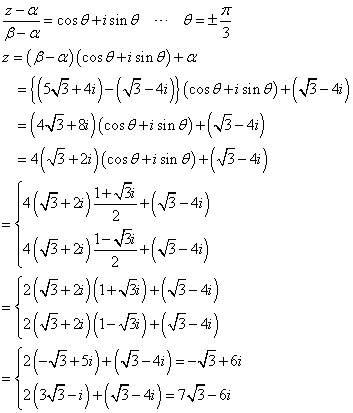
(3)


O(0)、A(α)、B(β)、D(z1)、F(z2)とする。
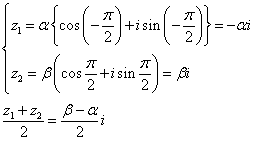
これが点Mを表す複素数である。
一方、線分ABを、AがOに重なるように平行移動したものを、OB'とすれば、B'(β-α)である。
したがって、B'をOを中心に反時計回りにπ/2回転し、長さを半分にした点が、Mであることがわかる。よって、示された。
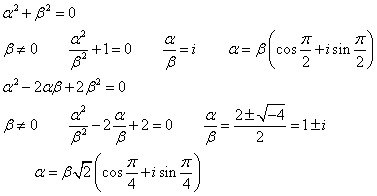
(1)AはBをOのまわりにπ/2回転した点であるから、OA=OB、かつ、∠AOB=90°の、直角二等辺三角形である。
(2)AはBをOのまわりにπ/4回転し、√2倍に拡大した点であるから、OA=AB、かつ、∠OAB=90°の、直角二等辺三角形である。

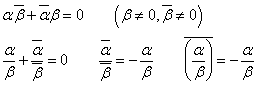
これは、α/βが純虚数だと言っている。すなわち、B(β)を原点O(0)のまわりに、±π/2回転したうえ、r倍拡大すれば、A(α)になる、と言っている。
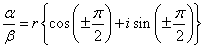
したがって、OAとOBは、直交する。
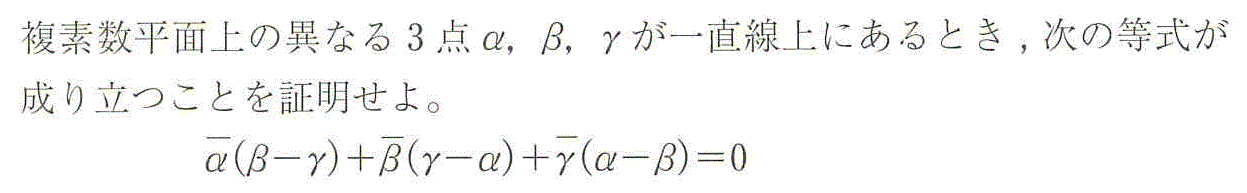
A(α)を中心にB(β)を、0またはπ回転したうえ、r倍に拡大した点が、C(γ)だと言っている。
すなわち、
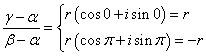
つまり、(γ-α)/(β-α)が「実数である」と言っている。すなわち、
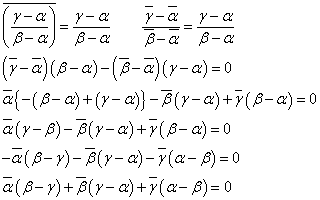
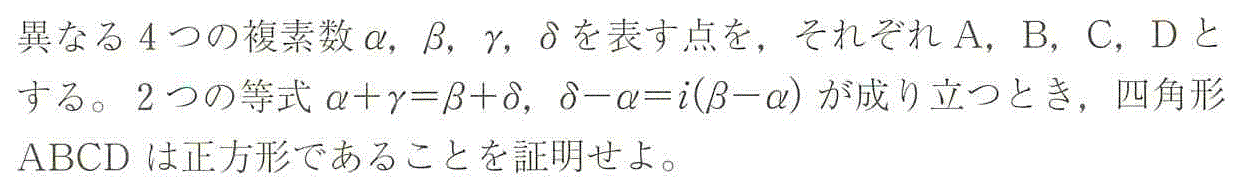
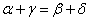 ・・・(1)
・・・(1)
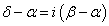 ・・・(2)
・・・(2)
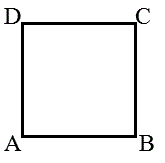
示したいのは次の二つである。
- B(β)をA(α)のまわりに「反時計回り」に、長さを変えずに、π/2回転した点が、D(δ)であること、すなわち、
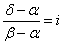
- A(α)をB(β)のまわりに「時計回り」に、長さを変えずに、π/2回転した点が、C(γ)であること、すなわち、
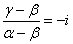
(1),(2)を、次のように変形して(ii)を得る。
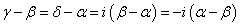
よって、示された。
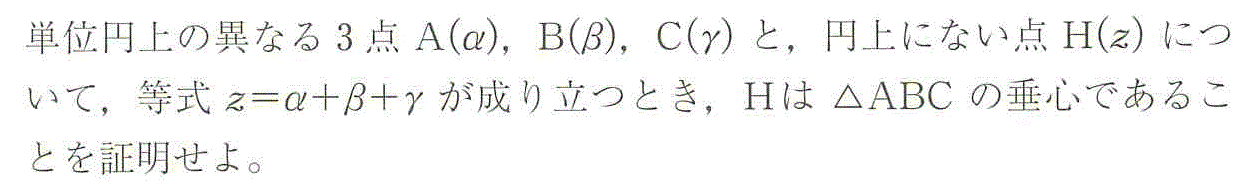
z=α+β+γに対して、AH⊥BC,BH⊥CA,CH⊥ABを示したい、すなわち、
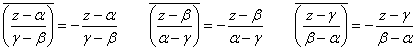
を示したい。ここで、A(α),B(β),C(γ)は単位円上の点であるから、
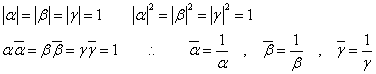
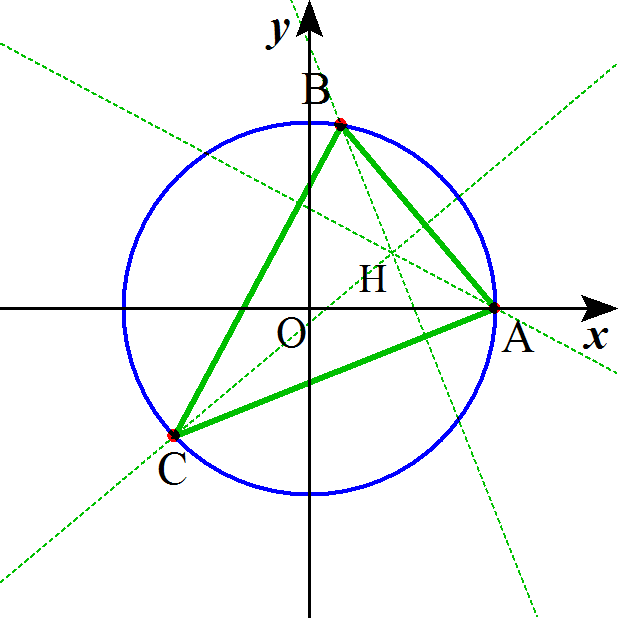
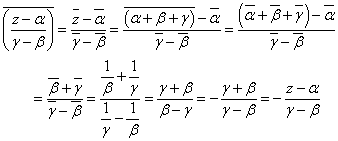
他も同様である。
- z4を、z3のまわりに「反時計回り」にθ回転し、r倍に拡大した点がz2、
- z2を、z1のまわりに「反時計回り」にφ回転し、r'倍に拡大した点がz4、
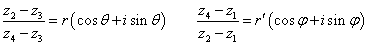

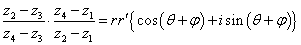
であるから、4点が同一円周上にあることを示すには、θ+φ=πを、すなわち、左辺の複素数が、実数であることを示せばよい。
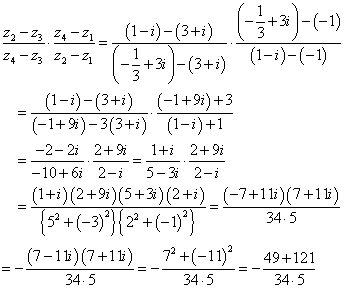
以上、示された。