- 3で割ると2余る
- 5で割ると3余る
- 7で割ると4余る
求める整数をxとして、
x=3k+2・・・(1)
x=5l+3・・・(2)
x=7m+4・・・(3)
を満たす、整数k,l,mの関係を知りたい。
(1)(2)より、3k+2=5l+3すなわち、3k-5l=1・・・(4)
(2)(3)より、5l+3=7m+4すなわち、5l-7m=1・・・(5)
3と5、および、5と7は、それぞれ「互いに素」であるから、1次不定方程式(4)(5)はいずれも整数解を持つ。
まず、それぞれの「特別解」、「一般解」を求めることから始める。
5=3+2・・・2=5-3
3=2+1・・・1=3-2
したがって、
1=3-2
1=3-(5-3)
1=3×2-5×1
「特別解」(k,l)=(2,1)
3k-5l=1・・・(4)
3・2-5・1=1・・・(4')
3(k-2)-5(l-1)=0・・・(4)-(4')
3(k-2)=5(l-1)
3,5は互いに素だから、整数iを用いて、次の「一般解」を得る。
(k,l)=(5i+2,3i+1)・・・(6)
同様に、
7=5+2・・・2=7-5
5=2×2+1・・・1=5-2×2
したがって、
1=5-2×2
1=5-(7-5)×2
1=5×3-7×2
「特別解」(l,m)=(3,2)
5l-7m=1・・・(5)
5・3-7・2=1・・・(5')
5(l-3)-7(m-2)=0・・・(5)-(5')
5(l-3)=7(m-2)
5,7は互いに素だから、整数jを用いて、次の「一般解」を得る。
(l,m)=(7j+3,5j+2)・・・(7)
ここで、(6)(7)のlが共通であることから、
3i+1=7j+3
すなわち、
3i-7j=2
3,7は互いに素であるから、
3i'-7j'=1
は整数解をもつ。「特別解」として(i',j')=(-2,-1)
したがって、(i,j)の特別解は、(i,j)=(-4,-2)
3i-7j=2・・・(8)
3(-4)-7(-2)=2・・・(8')
3(i+4)-7(j+2)=0・・・(8)-(8')
こうして、整数nを用いて、
(i,j)=(7n-4,3n-2)
これらを(6)(7)に戻せば、ただ一つの整数nを用いて、整数k,l,mが、したがって、求める整数xが、表現できることになる。
k=5i+2=5(7n-4)+2=35n-18
l=7j+3=7(3n-2)+3=21n-11
m=5j+2=5(3n-2)+2=15n-8
そして、
x=3k+2=5l+3=7m+4=105n-52
- x>0ならば、n=1,2,3.・・・、その最小のものは、n=1のときで、x=53
- x<0ならば、n=0,-1,-2.・・・、その最大のものは、n=0のときで、x=-52
- a,b,cの最大公約数は6である。
- b,cの最大公約数は30、最小公倍数は420である。
- a,bの最小公倍数は180である。
条件Bより、b=30b',c=30c'、ただし、b',c'は互いに素、と書くことができ、さらに、
420=30b'c'
すなわち、
b'c'=14
であることがわかる。
b<c、すなわち、b'<c'だから、可能性は次の二つに限られる、すなわち、
(b,c)=(1,14),(2,7)
- (b,c)=(1,14)のとき
条件Aより、b=6×5、c=6×5×14、に対して、a=6a'、ただし、a'には5を因数にもたないという制限があることがわかる。
条件Cより、180=6×5×a'、すなわち、a'=6となる。
このとき、(a,b,c)=(36,30,420)となるから、これは、条件a<b<cに反する。 - (b,c)=(2,7)のとき
条件Aより、b=6×5×2、c=6×5×7、に対して、a=6a'、ただし、a'には5を因数にもたないという制限があることがわかる。
したがって、a,bの最大公約数は、6であるか、または、12であるか、二つの可能性がある。- a,bの最大公約数が6であるとき、条件Cより、
180=6×a'×5×2、すなわち、a'=3
このとき、(a,b,c)=(18,60,210) - a,bの最大公約数が12であるとき、条件Cより、
180=6×a'×5、すなわち、a'=6
このとき、(a,b,c)=(36,60,210)
よって、(a,b,c)=(18,60,210),(36,60,210) - a,bの最大公約数が6であるとき、条件Cより、
19x+29y=450・・・(1)
19,29は互いに素であるから、
19u+29v=1・・・(2)
は、整数解をもつ。その特別解の一つは(ユークリッド互除法を用いた詳細を省略すると)、(u,v)=(-3,2)である。
したがって、(1)の特別解の一つは、(x,y)=(450u,450v)=(-1350,900)となる。
19x+29y=450・・・(1)
19(-1350)+29・900=450・・・(1')
19(x+1350)+29(y-900)=0・・・(1)-(1')
-19(x+1350)=29(y-900)
19と29とは互いに素であるから、整数kを用いて、次のように書くことができる。
(x,y)=(29k-1350,900-19k)
ここで、題意から、x≧0、y≧0、すなわち、
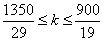
これを満たす整数は、k=47のみ、よって、(x,y)=(13,7)を得る。
[別解](2)の特別解を450倍すると、あまりにも数字が大きくなりすぎるので、予め、次のような工夫をしてもよい。
- 450を29で割ってみると、
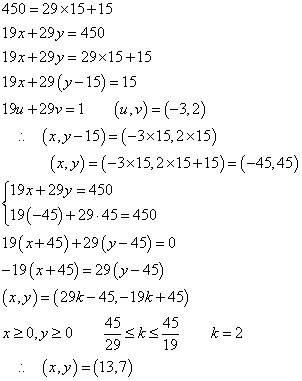
- 450を19で割ってみると、
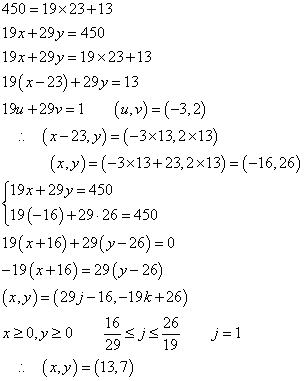
[注]「合同式」を用いても、この例ではうまくいかないようである。
450≡29y (mod 19)
すなわち、
13≡10y (mod 19)
とか、
-6≡10y (mod 19)
-6≡-9y (mod 19)
いろいろやってみても、yの係数が消えないので、有難味がなさそうなのである。mod 29でやってみても同様。
問題集などに、「合同式を用いた別解」が紹介されている場合が多いが、数字の設定によってうまくいくときとそうでもない時があるようで、「原則」としては、「ユークリッド互除法」による1次不定方程式の解法、で、すべてが解決するはずである。
私がうっかり間違えてしまったのは、右辺が1のときの特別解を、この問題ならば、450倍する「タイミング」、であった。まず450倍して「特別解」を得てからそれを「一般解」にしないと、逆にすると、定数項も450倍されてしまうから、すべての解をカバーできなくなってしまうのだ!
そう、その今後の研究課題であったが、さて、ほんのちょっとだけ、変更して、次のようにしてみよう。

こういう場合に「合同式」を使えば簡単!、などと、受験参考書は「称揚」するのだが、それは単に、この恣意的な数字の選び方がうまくいったから、だけのことであって、では、例えば、
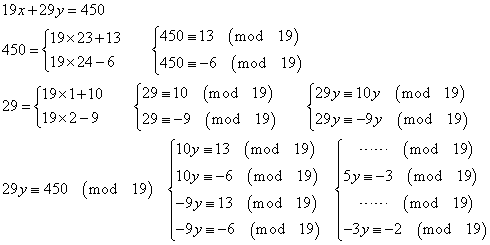
ならば、決して、yを○k+△と表す方法が存在せず、だから、この場合は、「合同式」の有難味がない、ならば、私たちは、「どんな場合に、『合同式』の有難味があるのか?」知りたいのが「人情」なのだが、どうも、「彼ら」は、それを説明する時間を割くことには、あまり積極的ではないらしい、ということが、わかった、訳である。