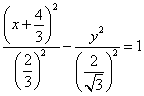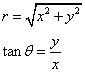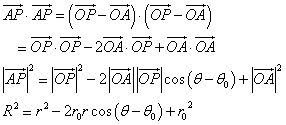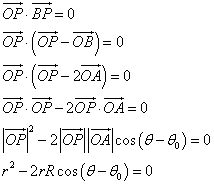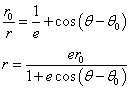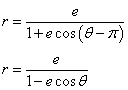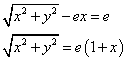定義:2点からの距離の「和」が一定であるような点の軌跡。
- 2点(焦点)がx軸上
C(c,0),C'(-c,0)からの距離の和が2aであるような点P(x,y)の軌跡(ただし、a>c:三角形の2辺の和は他の1辺より大きい)
PC+PC'=2a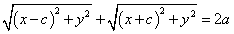
左辺第2項を移項して、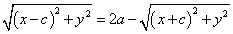
両辺を2乗すると、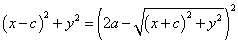
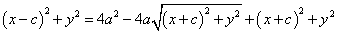
両辺からいくつかの項が消える。両辺を4で割る。根号のついた項のみ左辺にまとめ、再び両辺を2乗する。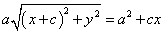
a2{(x+c)2+y2}=a4+2a2cx+c2x2
(a2-c2)x2+a2y2=a2(a2-c2)
ここで、a2-c2=b2とおくと、(明らかに0<b<a)
b2x2+a2y2=a2b2
両辺をa2b2で割り、
が、得られた。0<b<aのとき、 
は、x軸上に焦点を持つ楕円を表す。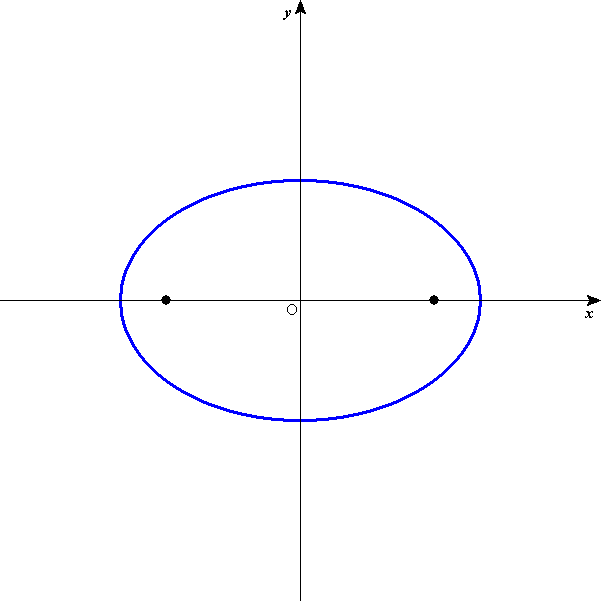
長半径:a、短半径:b
焦点: C( 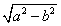
,0),C'(- 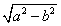
,0)
- 2点(焦点)がy軸上
C(0,c),C'(0,-c)からの距離の和が2bであるような点P(x,y)の軌跡(ただし、b>c:三角形の2辺の和は他の1辺より大きい)
PC+PC'=2b
左辺第2項を移項して、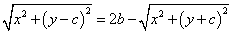
両辺を2乗すると、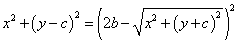
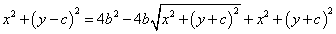
両辺からいくつかの項が消える。両辺を4で割る。根号のついた項のみ左辺にまとめ、再び両辺を2乗する。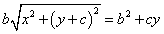
b2{x2+(y+c)2}=b4+2b2cy+c2y2
b2x2+(b2-c2)y2=b2(b2-c2)
ここで、b2-c2=a2とおくと、(明らかに0<a<b)
b2x2+a2y2=a2b2
両辺をa2b2で割り、
が、得られた。0<a<bのとき、 
は、y軸上に焦点を持つ楕円を表す。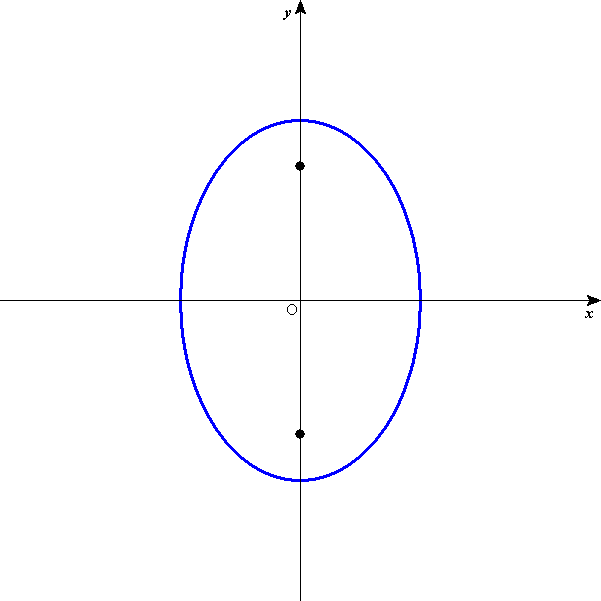
長半径:b、短半径:a
焦点: C(0, 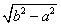
,C'(0,- 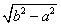
)
定義:2点からの距離の「差」が一定であるような点の軌跡。
- 2点(焦点)がx軸上
C(c,0),C'(-c,0)からの距離の差が2aであるような点P(x,y)の軌跡(ただし、a<c:三角形の2辺の差は他の1辺より小さい)
|PC-PC'|=2a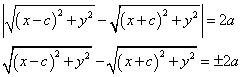
左辺第2項を移項して、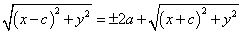
両辺を2乗すると、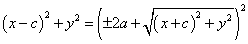
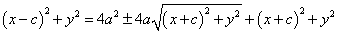
両辺からいくつかの項が消える。両辺を4で割る。根号のついた項のみ左辺にまとめ、再び両辺を2乗する。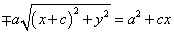
a2{(x+c)2+y2}=a4+2a2cx+c2x2
(c2-a2)x2-a2y2=a2(c2-a2)
ここで、c2-a2=b2とおくと、
b2x2-a2y2=a2b2
両辺をa2b2で割り、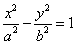
が、得られた。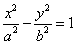
は、x軸上に焦点を持つ双曲線を表す。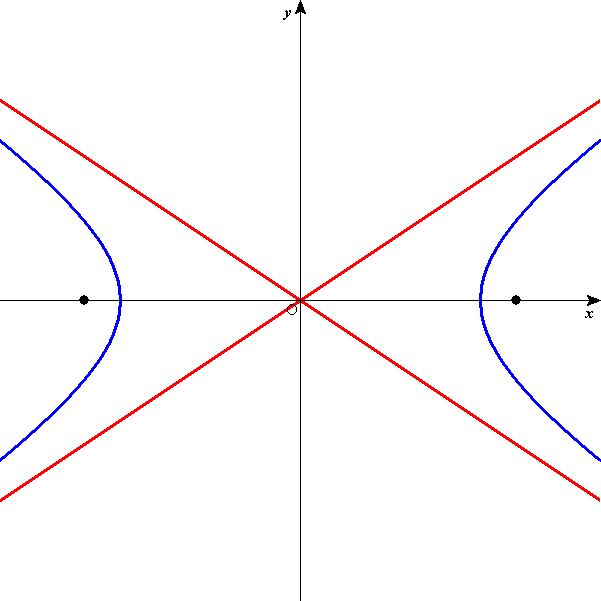
頂点:(a,0),(-a,0)
焦点: C( 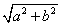
,0),C'(- 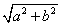
,0) 漸近線: 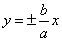
- 2点(焦点)がy軸上
C(0,c),C'(0,-c)からの距離の差が2bであるような点P(x,y)の軌跡(ただし、b<c:三角形の2辺の差は他の1辺より小さい)
|PC-PC'|=2b
左辺第2項を移項して、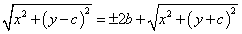
両辺を2乗すると、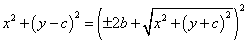
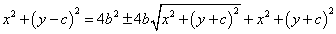
両辺からいくつかの項が消える。両辺を4で割る。根号のついた項のみ左辺にまとめ、再び両辺を2乗する。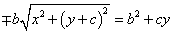
b2{x2+(y+c)2}=b4+2b2cy+c2y2
b2x2-(c2-b2)y2=-b2(c2-b2)
ここで、c2-b2=a2とおくと、
b2x2-a2y2=-a2b2
両辺をa2b2で割り、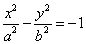
が、得られた。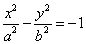
は、y軸上に焦点を持つ双曲線を表す。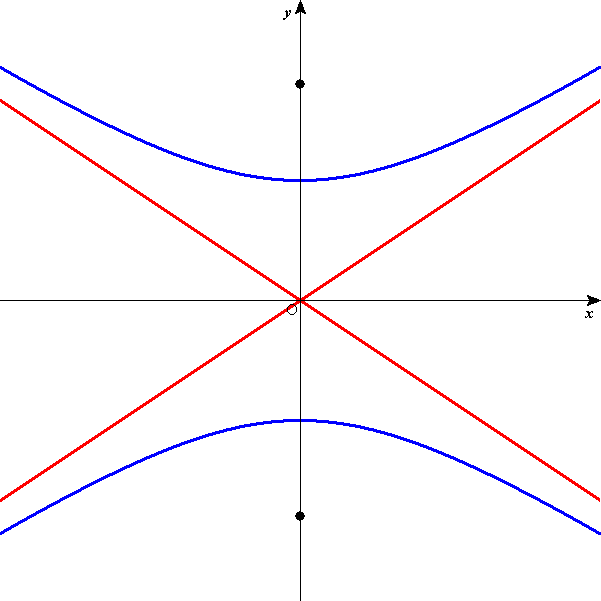
頂点:(0,b),(0,-b)
焦点: C(0, 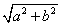
),C'(0,- 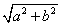
) 漸近線: 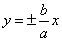
定義:1点からの距離と定直線との距離が等しいような点の軌跡。
- 1点(焦点)がx軸上・定直線(準線)がy軸に平行
点C(c,0)との距離,直線x=-cへの距離が等しい点P(x,y)の軌跡
Pから直線x=-cへ下ろした垂線の足をHとすると、H(-c,y)であるから、
PC=PH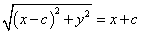
両辺を2乗して、
(x-c)2+y2=(x+c)2
y2=4cxy2=4cx
は、x軸上に焦点を持ち、
y軸に平行な直線を準線とする放物線を表す。
頂点:(0,0)、 焦点:C(c,0)、 準線:x=-c - 1点(焦点)がy軸上・定直線(準線)がx軸に平行
点C(0,c)との距離,直線y=-cへの距離が等しい点P(x,y)の軌跡
Pから直線y=-cへ下ろした垂線の足をHとすると、H(x,-c)であるから、
PC=PH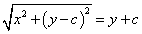
両辺を2乗して、
x2+(y-c)2=(y+c)2
x2=4cyx2=4cy
は、y軸上に焦点を持ち、
x軸に平行な直線を準線とする放物線を表す。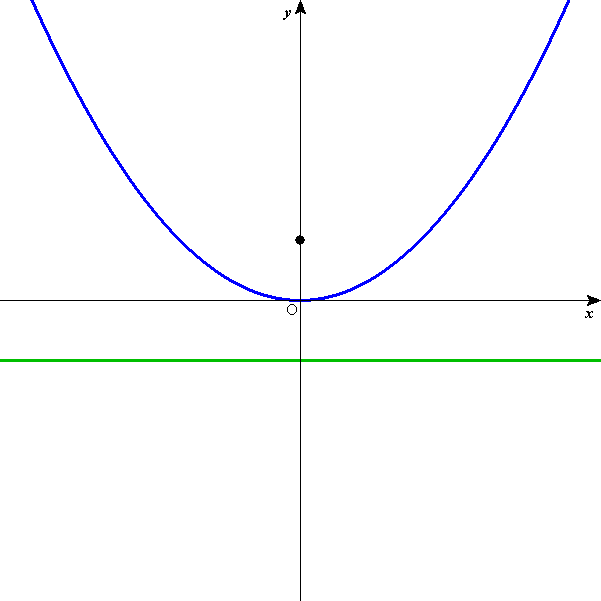
頂点:(0,0)、 焦点:C(0,c)、 準線:y=-c
1つのxの値に対して、yの値が1つ定まるとき、「yはxの関数である」という。
この事実が、はっきりとした形で表されている表現形式、つまり、yがxの「関数」として表現されている式を「陽関数」という。
y=f(x)
これに対して、「yはxの関数である」かも知れないが、その事実が「隠されている」表現形式を「陰関数」という。
g(x,y)=0
たとえば、xy平面上の直線は、
y=mx+n・・・①
ax+by+c=0・・・②
という二つの表現形式が考えられるが、①が「陽関数」表現、②が「陰関数」表現である。
これら2つの表現方法の、メリット・デメリットを考えてみよう。
- ①には決して表現できない直線が存在する。すなわち、y軸に平行な直線x=r、ちなみに、この直線上の点については、「1つのxの値に対して、yの値が1つ定まる」とはいえないから、yはxの関数ではない、から当然である。
- ②はy軸に平行な直線を含むxy平面上のすべての直線を表現できる。しかし、0の定数倍がすべて0である以上、②式を定数倍しても、それらの式はすべて同値であり、「一つに定まらない」というデメリットがある。
x2+y2=r2
という、もっともシンプルな「2次曲線」について考える。
xの値を1つ定めても、点(±r,0)以外では、yの値は必ず2つあり、「1つに定まらない」から、「yはxの関数である」とはいえない。この図形を「陽関数」で表現するとすれば、次の2つの関数となる。

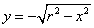
- 楕円

両辺をxで微分すると、
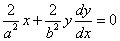
- y≠0のとき
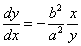
点(x0,y0)における接線は、
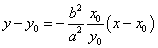
a2y0(y-y0)+b2x0(x-x0)=0
b2x0x+a2y0y-(b2x02+a2y02)=0
ここで、点(x0,y0)は、楕円上の点であるから、
b2x02+a2y02=a2b2
したがって、
b2x0x+a2y0y=a2b2・・・①
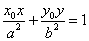 ・・・①'
・・・①'
- y=0のとき、すなわち、点(±a,0)における接線は、
x=±a
これは、①に含まれる。
- y≠0のとき
- 双曲線
-
x軸上に焦点を持つ双曲線
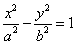
両辺をxで微分すると、

- y≠0のとき
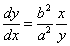
点(x0,y0)における接線は、
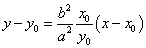
a2y0(y-y0)-b2x0(x-x0)=0
b2x0x-a2y0y-(b2x02-a2y02)=0
ここで、点(x0,y0)は、双曲線上の点であるから、
b2x02-a2y02=a2b2
したがって、
b2x0x-a2y0y=a2b2・・・②
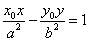 ・・・②'
・・・②'
- y=0のとき、すなわち、点(±a,0)における接線は、
x=±a
これは、②に含まれる。
- y≠0のとき
-
y軸上に焦点を持つ双曲線
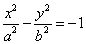
両辺をxで微分すると、

y≠0だから、
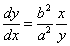
点(x0,y0)における接線は、
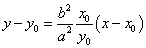
a2y0(y-y0)-b2x0(x-x0)=0
b2x0x-a2y0y-(b2x02-a2y02)=0
ここで、点(x0,y0)は、双曲線上の点であるから、
b2x02-a2y02=-a2b2
したがって、
b2x0x-a2y0y=-a2b2・・・③
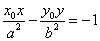 ・・・③'
・・・③'
-
x軸上に焦点を持つ双曲線
- 放物線
-
x軸上に焦点を持ち、y軸に平行な直線を準線とする放物線
y2=4cx
両辺をxで微分すると、
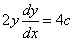
- y≠0のとき
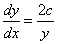
点(x0,y0)における接線は、
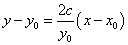
y0(y-y0)=2c(x-x0)
y0y-y02=2cx-2cx0
ここで、点(x0,y0)は、放物線上の点であるから、
y02=4cx0
したがって、
y0y-4cx0=2cx-2cx0
y0y=2c(x+x0)・・・④ - y=0のとき、すなわち、点(0,0)における接線は、
x=0
これは、④に含まれる。
- y≠0のとき
-
y軸上に焦点を持ち、x軸に平行な直線を準線とする放物線
x2=4cy
両辺をxで微分すると、
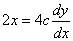
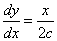
点(x0,y0)における接線は、
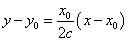
2c(y-y0)=x0(x-x0)
2cy-2cy0=x0x-x02
ここで、点(x0,y0)は、放物線上の点であるから、
x02=4cy0
したがって、
2cy-2cy0=x0x-4cy0
x0x=2c(y+y0)・・・⑤
-
x軸上に焦点を持ち、y軸に平行な直線を準線とする放物線
| 点(x0,y0)における接線 | ||
| 焦点がx軸上 | 焦点がy軸上 | |
| 楕円 | 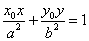 | 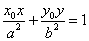 |
| 双曲線 | 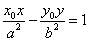 | 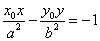 |
| 放物線 | y0y=2c(x+x0) | x0x=2c(y+y0) |
変数x,yに関する2次式、すなわち、x2の項、xyの項、y2の項、xの項、yの項、定数項、で表現される式、
ax2+bxy+cy2+dx+ey+f=0
で表される図形を「2次曲線」と呼んでいる。xにある定数を代入した式はyの2次方程式だから、1つのxの値に対して、yの値が1つ定まる、とはいえず、yはxの関数ではない。このような式が表す曲線は?
円錐を、平面で切ったときにできる曲線群を、「円錐曲線」と呼んでいる。
母線を含む平面に平行な平面で切ると「放物線」、底面とのなす角がこれよりも小さい平面で切ると「楕円」、底面に平行になれば、「楕円」の特別な場合として「円」、反対に底面とのなす角がこれよりも大きい平面で切ると「双曲線」が得られる。これと平行で、円錐の頂点を含む平面で切れば、「2個の直線」が得られ、これらは、「双曲線」の「漸近線」をなす。
「円錐曲線」はすべて、変数x,yに関する2次式で表される。
以下の二つの例で、これは少しも「証明」ではないが、確認してみよう。
-
[例題1]
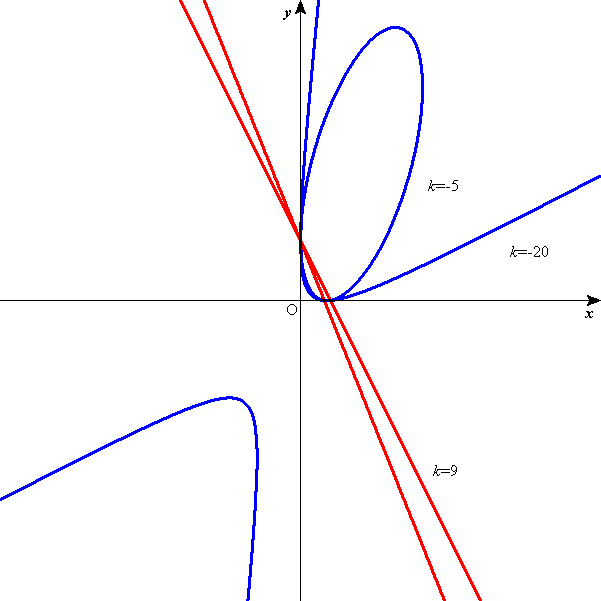
10x2+kxy+2y2-9x-4y+2=0が2直線を表すときのkの値を求めよ。ただし、kは整数とする。[03 自治医大]
[解答]
与えられた式は、
2y2+(kx-4)y+(10x2-9x+2)=0・・・①
2y2+(kx-4)y+(5x-2)(2x-1)=0
と変形できるから、この式が、x,yの1次式の積に「因数分解」されるとすると、次の4つの可能性(複号同順)しかない。
{2y±(2x-1)}{y±(5x-2)}=0
{2y±(5x-2)}{y±(2x-1)}=0
このなかで、yの1次の係数が-4となるのは、
(2y+5x-2)(y+2x-1)=0
のみである。これを展開すると、
10x2+9xy+2y2-9x-4y+2=0
であるから、k=9
[別解]
①式がx,yの1次式の積に「因数分解」されるとすれば、①をyの2次方程式として解いた解が、xの1次式でなければならない。
とすれば、「解の公式」のなかの「根号」の内部、
(kx-4)2-8(10x2-9x+2)
つまり①式の「解の判別式」が、xの「完全平方式」でなければならない。
①をyの2次方程式と見たときの、「解の判別式」をD1とする。
D1=(kx-4)2-8(10x2-9x+2)
D1=0はxについての2次方程式である。
これがxの完全平方式であるためには、D1=0をxについての2次方程式と見たときの「解の判別式」D2がD2=0を満たさなければならない。
D1=(k2-80)x2-8(k-9)x
D2=64(k-9)2
したがって、D2=0を満たすkは、k=9のみである。 -
[例題2]
点(x,y)を、原点を中心として、反時計回りにθだけ回転する1次変換を表す行列は、
である。これを用いて、以下の式が表す図形が、楕円であることを証明せよ。A= 
cosθ -sinθ 
sinθ cosθ
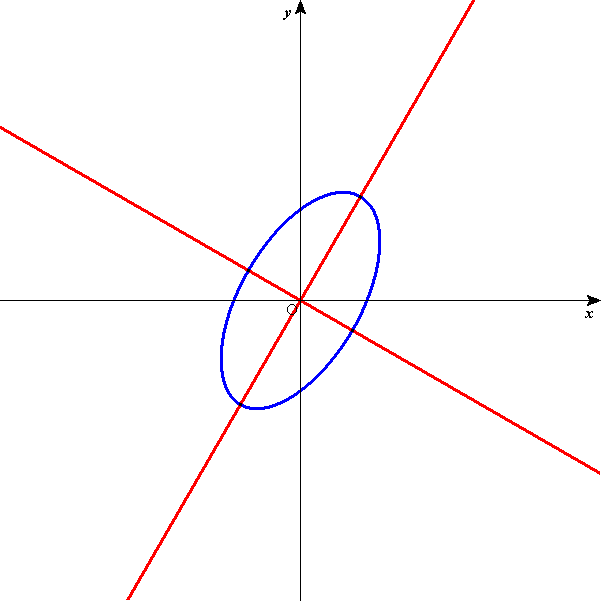
13x2-6√3xy+7y2-16=0
この図形が、ある図形を原点周りにθ回転して得られたものだとすれば、この図形上の任意の点(x,y)に対して、「元の図形」上の点(X,Y)は、次の関係を満たす。
x=Xcosθ-Ysinθ
y=Xsinθ+Ycosθ
13(Xcosθ-Ysinθ)2-6√3(Xcosθ-Ysinθ )(Xsinθ+Ycosθ)+7(Xsinθ+Ycosθ)2-16=0
(13cos2θ-6√3cosθsinθ+7sin2θ)X2+{-12cosθsinθ-6√3(cos2θ-sin2θ)}XY+(13sin2θ+6√3cosθsinθ+7cos2θ)X2-16=0・・・①
この式のXYの項の係数が0になるように回転角θを定めたい。
12cosθsinθ+6√3(cos2θ-sin2θ)=0
6sin2θ+6√3cos2θ=0
sin2θ+√3cos2θ=0
2sin(2θ+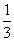 π)=0
π)=0
θは-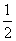 π≦θ<
π≦θ<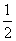 πの角だから、-
πの角だから、-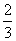 π≦2θ+
π≦2θ+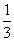 π<
π<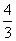 π
π
よって、θ=-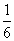 πまたは、
πまたは、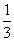 π
π
①に代入すると、- θ=-
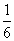 πのとき、
πのとき、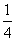 x2+y2=1
x2+y2=1
- θ=
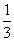 πのとき、x2+
πのとき、x2+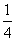 y2=1
y2=1
- θ=-
|
|
| 10x2+kxy+2y2-9x-4y+2=0の表す図形 | 13x2-6√3xy+7y2-16=0 の表す図形 |
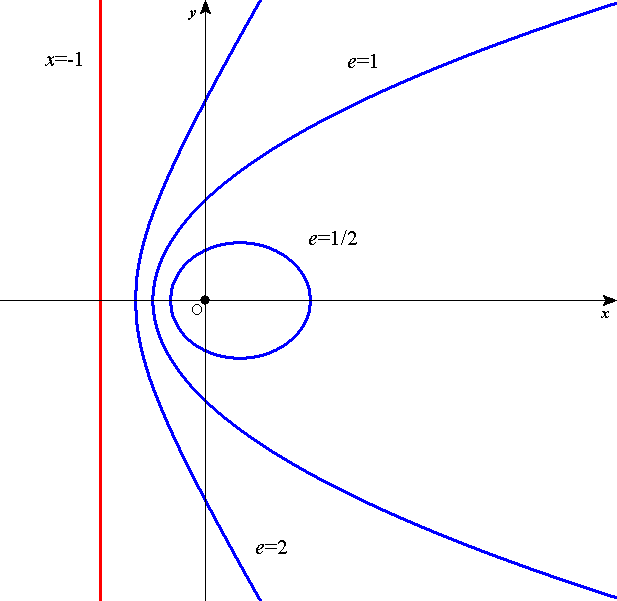
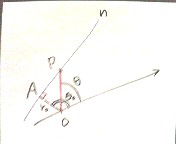
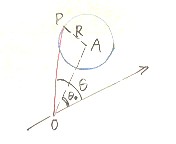
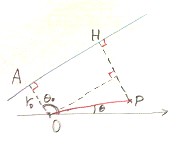
定点との距離と定直線との距離の比が一定である点の軌跡は、2次曲線であることが知られている。
定点との距離の、定直線との距離に対する比を「離心率」eとする。
「定点」として原点O、「定直線」として、x=-dを選ぶ。
動点P(x,y)から、直線x=-dに下ろした垂線の足をHとすると、H(-d,y)であるから、
PO/PH=e
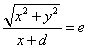
両辺に(x+d)をかけ、2乗すると、
x2+y2=e2(x+d)2
(1-e2)x2-2e2dx+y2-e2d2=0・・・①
または、
(e2-1)x2+2e2dx-y2+e2d2=0・・・②
となる。
- e=1のとき
①②は、
2dx-y2+d2=0
y2=2dx+d2
[例]d=1とすると、
y2=2x+1 - e<1のとき
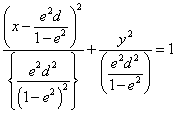
[例]e=1/2,d=1とすると、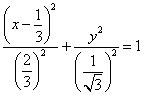
- e>1のとき
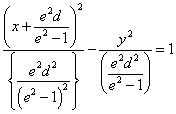
[例]e=2,d=1とすると、