

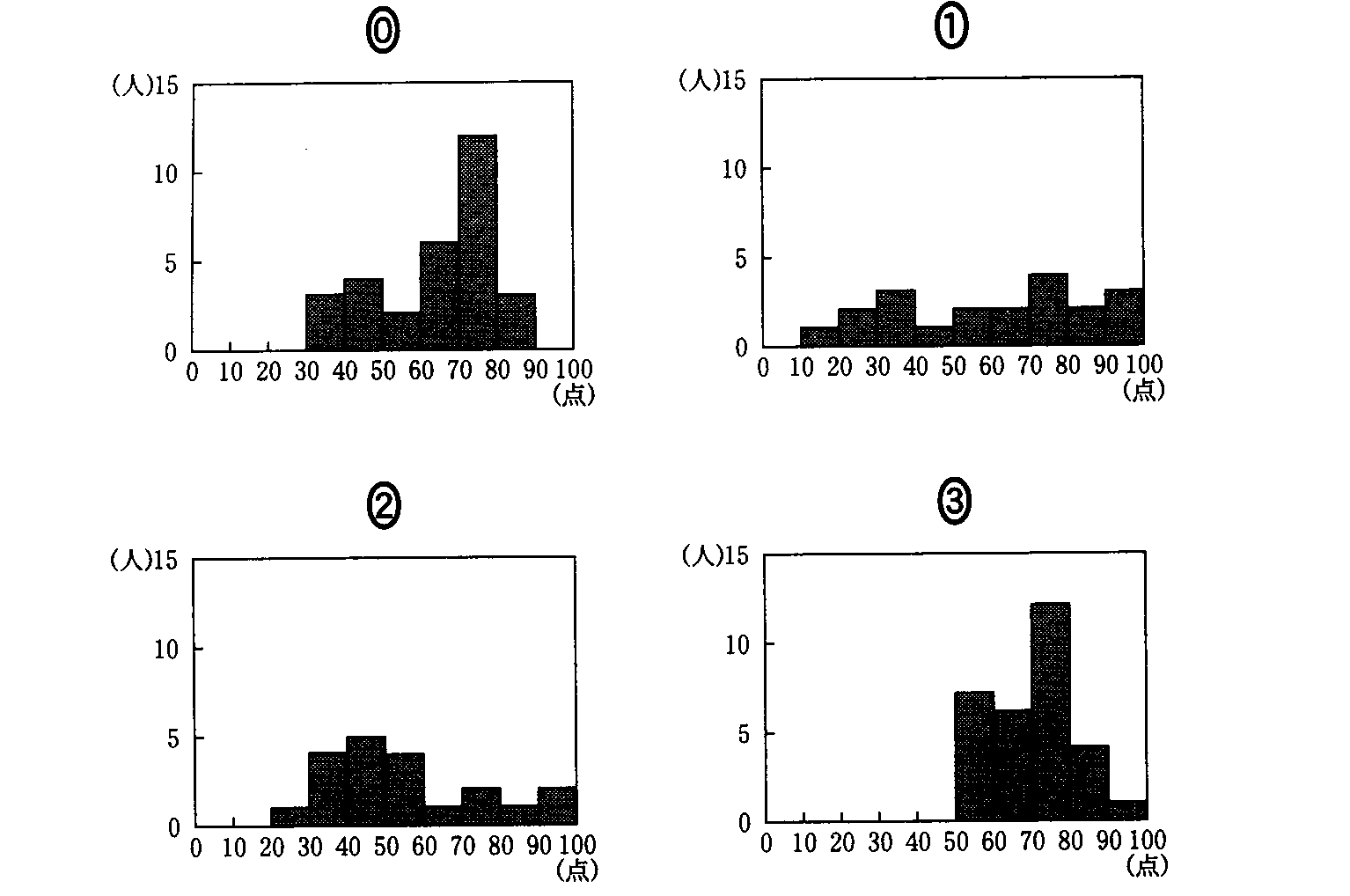


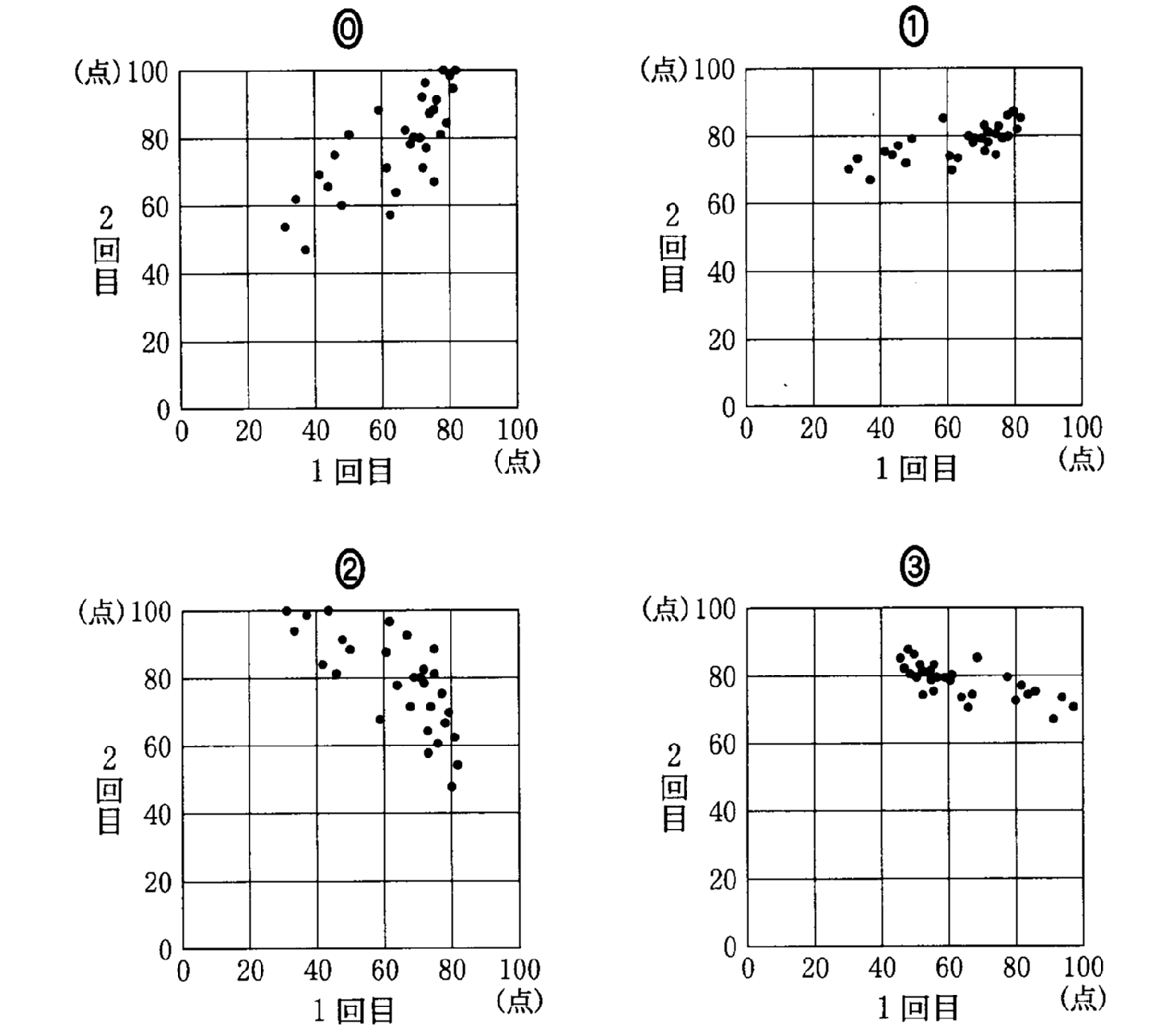

(2008追5)

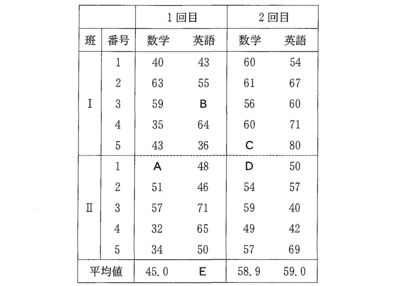





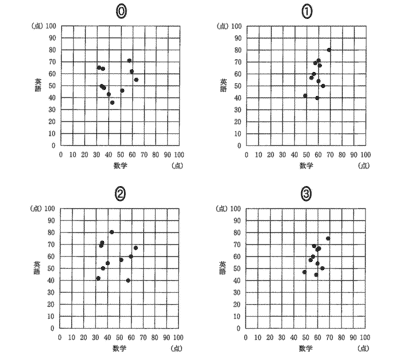


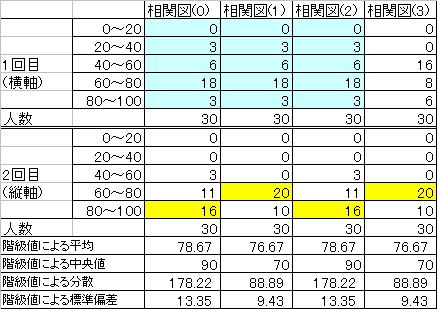
(2009本5)







(2008追5)










(2009本5)
1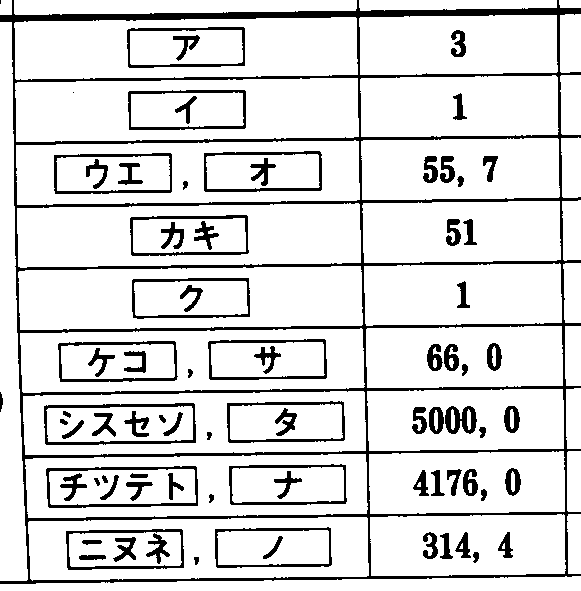 |
2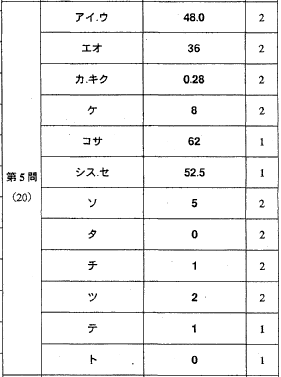 |
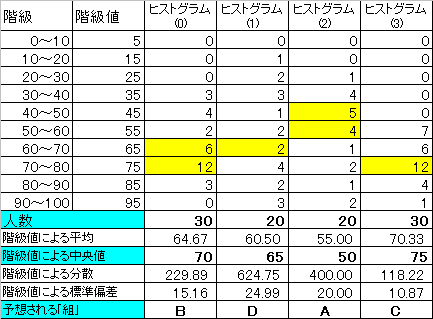
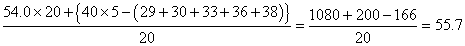
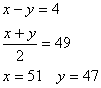

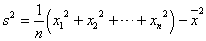
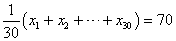
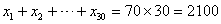
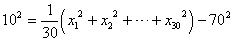
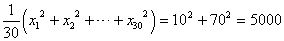
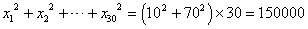
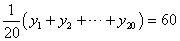
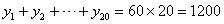
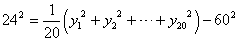
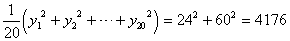
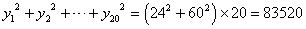
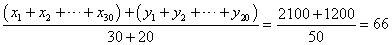


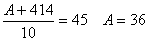

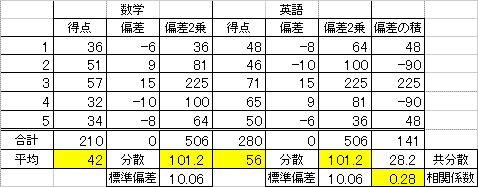
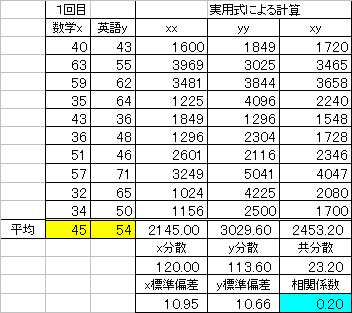
| 分散 | 偏差の「2乗」の平均 |
| 標準偏差 | 分散の平方根 |
| 共分散 | 偏差の「積」の平均 |
| 相関係数 | 共分散/(標準偏差の「積」) |
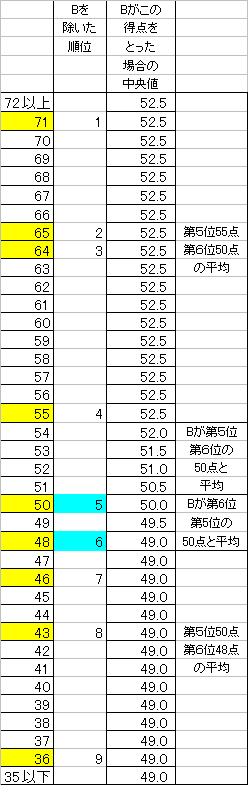 |
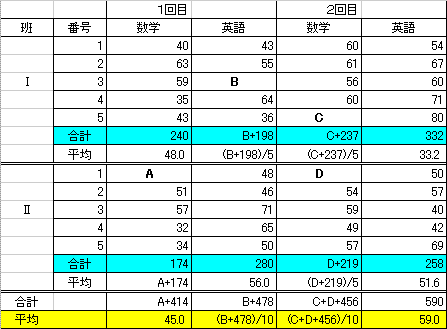
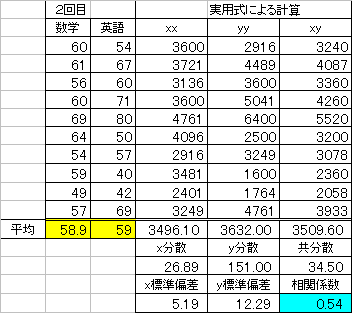
10人のデータの「中央値」であるから、第5位と第6位の生徒の点数の平均点を採用することになる。
Bを除く9人のデータでは、 第5位が50点、第6位が48点。
|
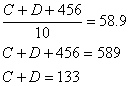
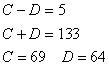
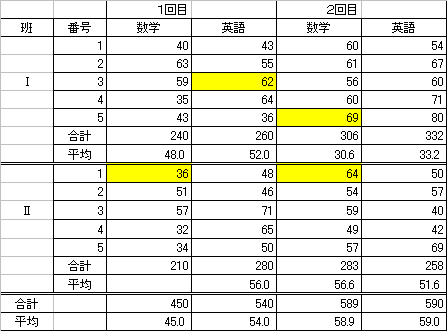
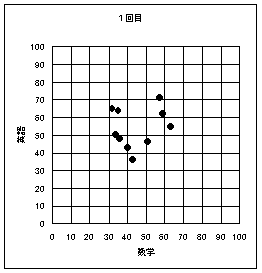 |
 |
 |
 |