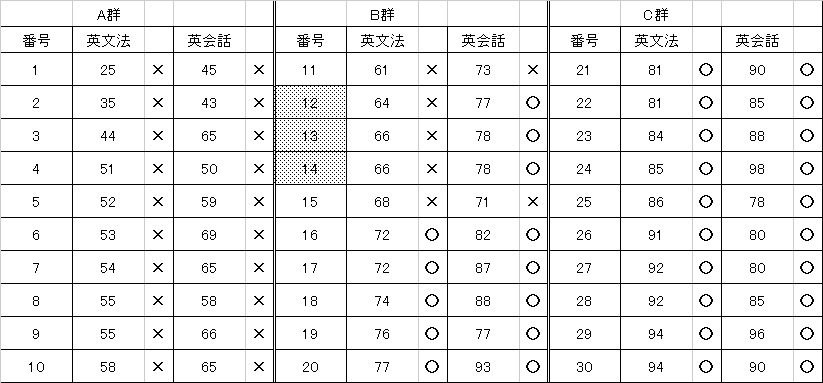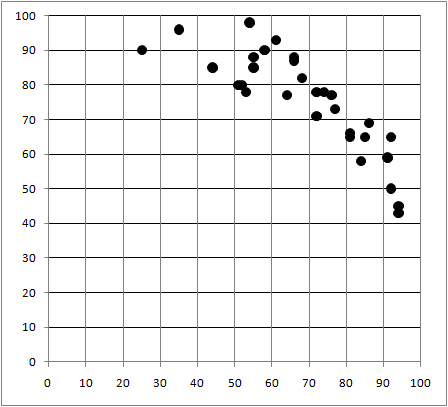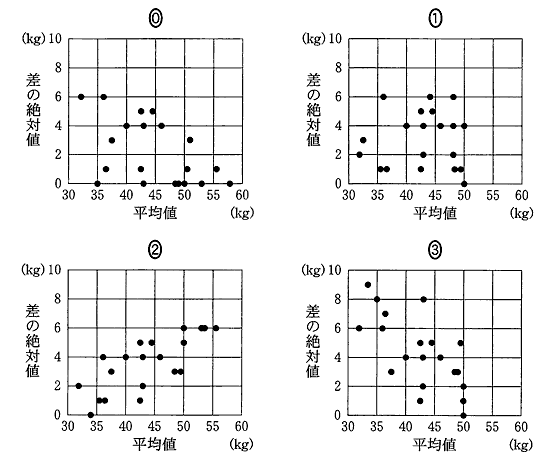

[2010本]
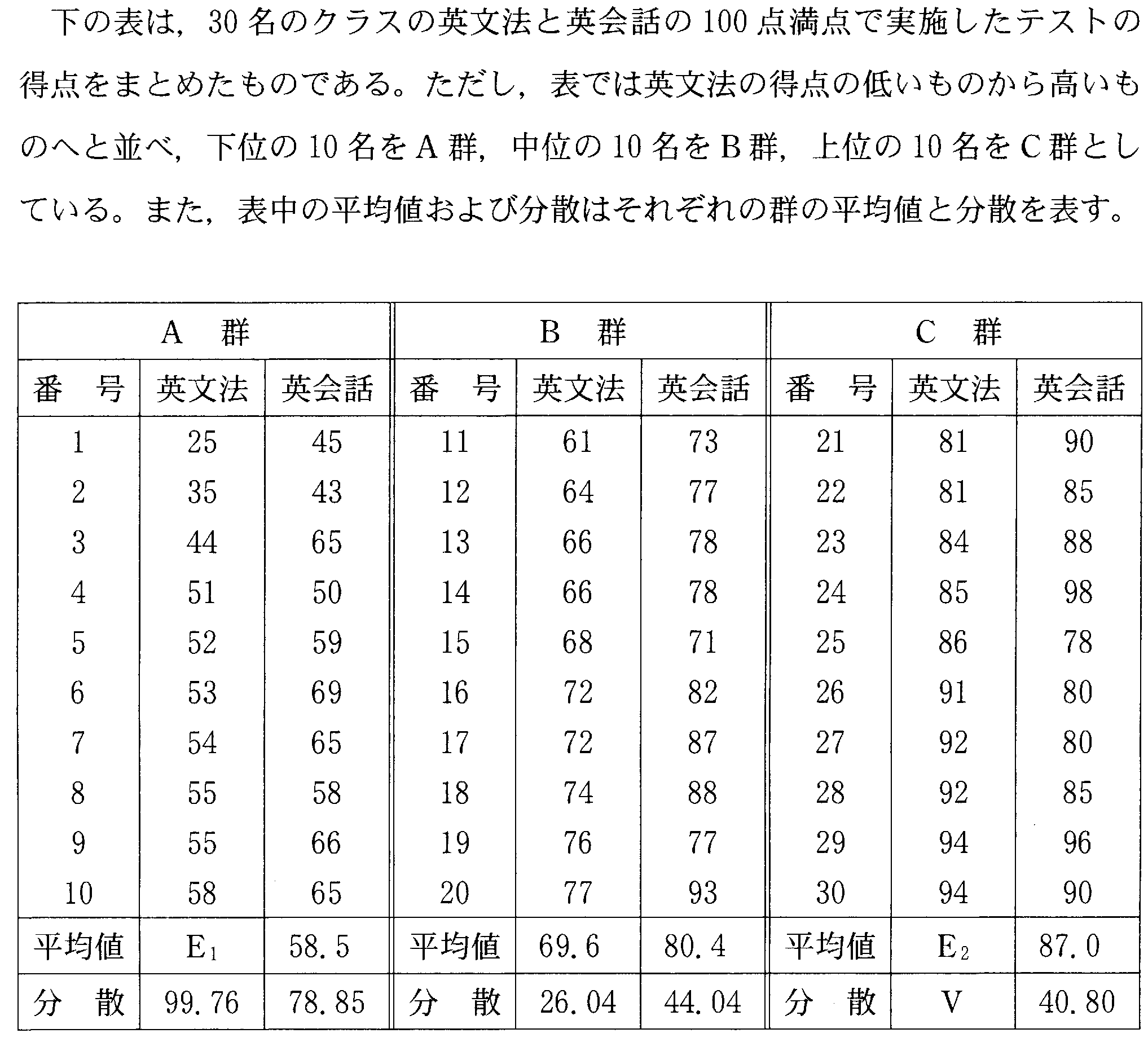


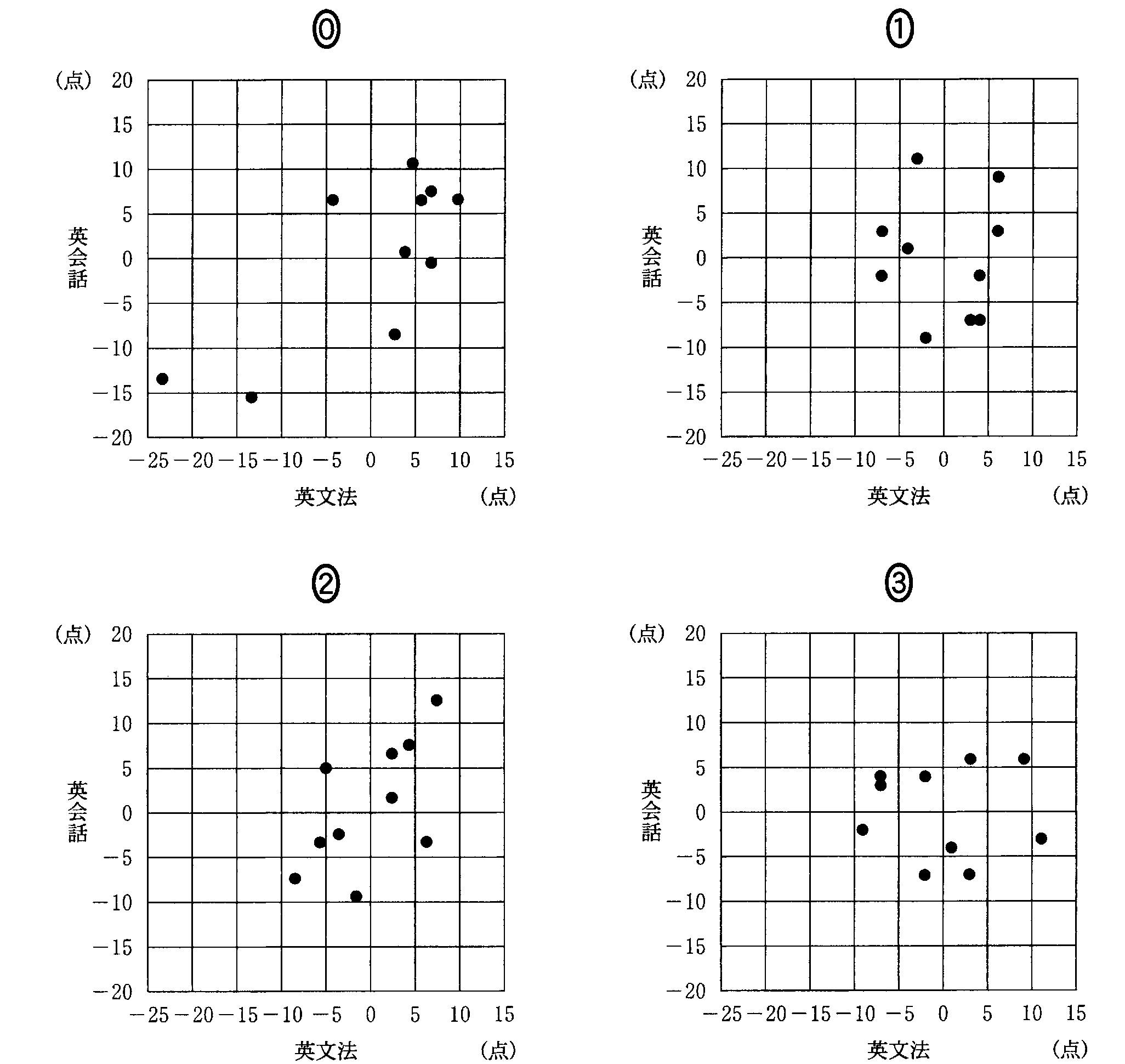

[2009追]
2010本 |
2009追 |










[2010本]





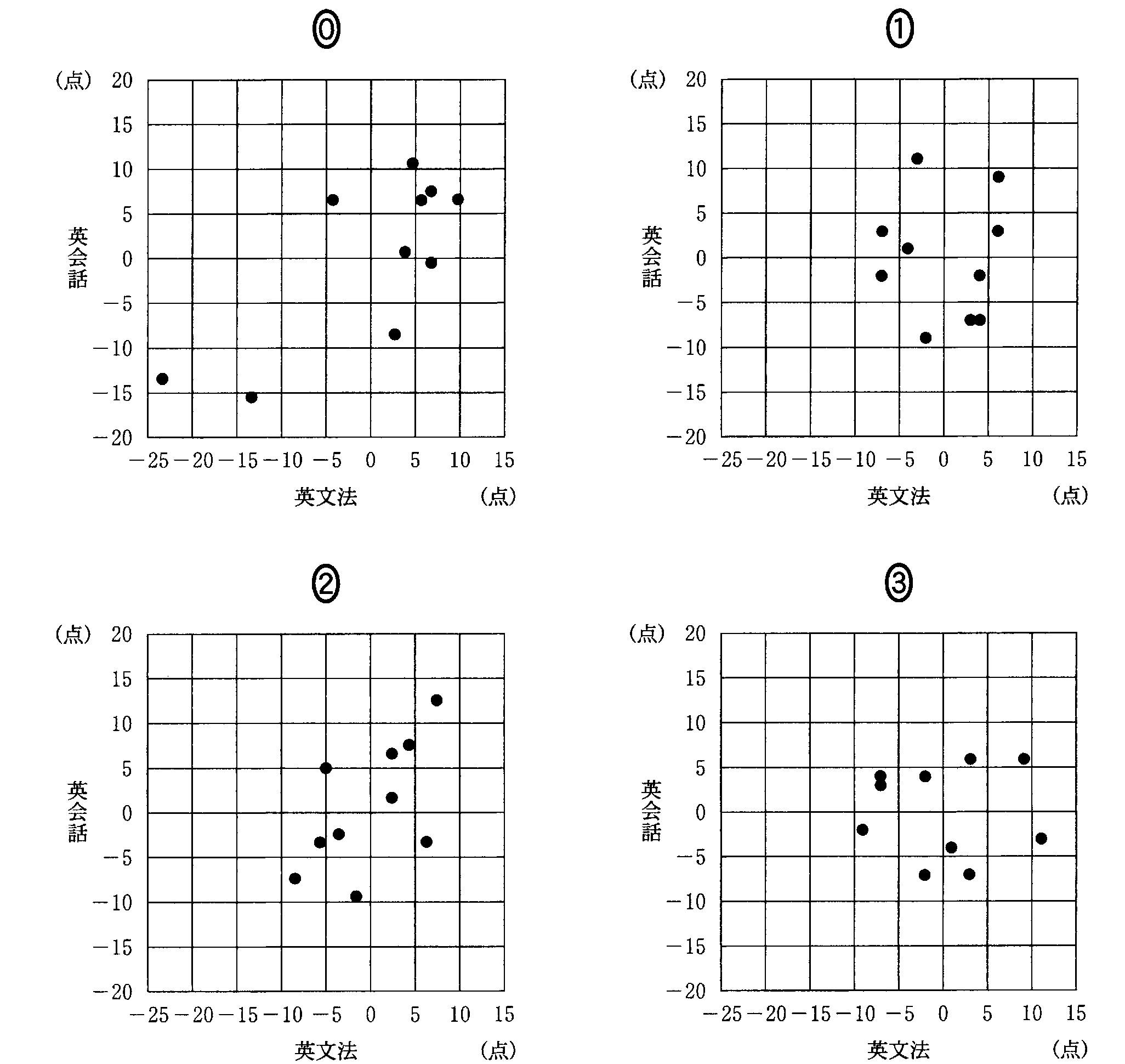


[2009追]
2010本 |
2009追 |
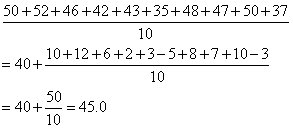
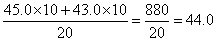
| 「中央値」 |
データを「得点」の高い順(降順)、または、低い順(昇順)に並べたとき、「中央」に来る値。
|
| 「分散」と「標準偏差」 |
|
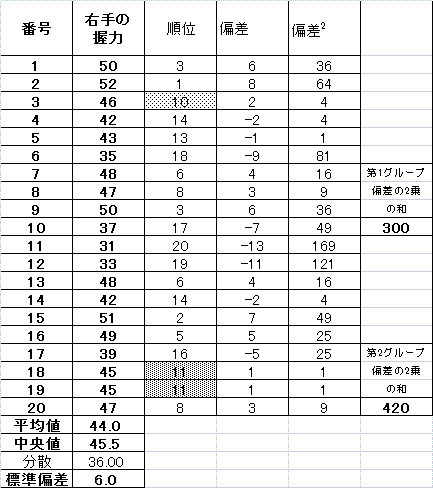 |
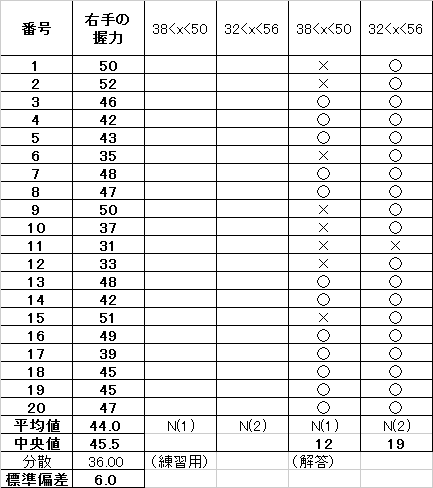
| 20人全体の「中央値」と「分散・標準偏差」の計算 |
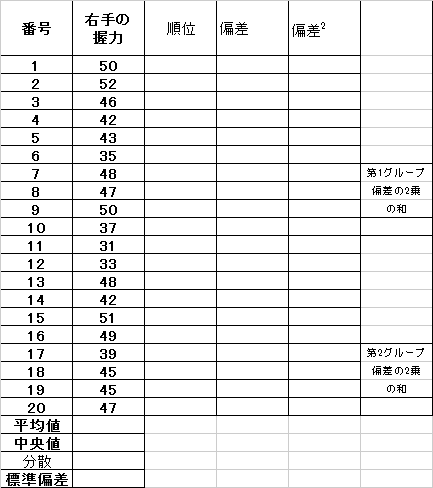 |
| 20人全体の「中央値」と「分散・標準偏差」の計算(練習用) |
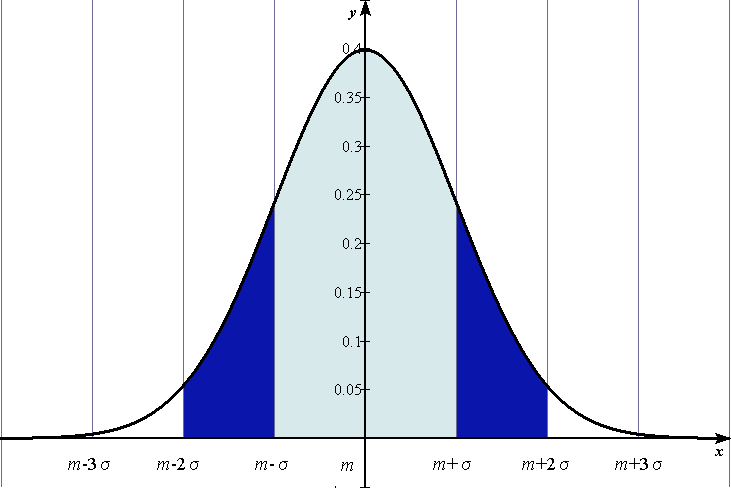
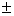 σ の間にそれぞれ34.1パーセント
σ の間にそれぞれ34.1パーセント
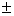 σ と m
σ と m 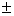 2σ の間にそれぞれ13.6パーセント
2σ の間にそれぞれ13.6パーセント
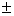 2σ と m
2σ と m 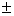 3σ の間に2.1パーセント
3σ の間に2.1パーセント
 3σ の外側にはそれぞれ0.1パーセント
3σ の外側にはそれぞれ0.1パーセント
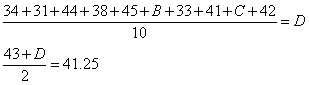
| 差 の 絶 対 値 | 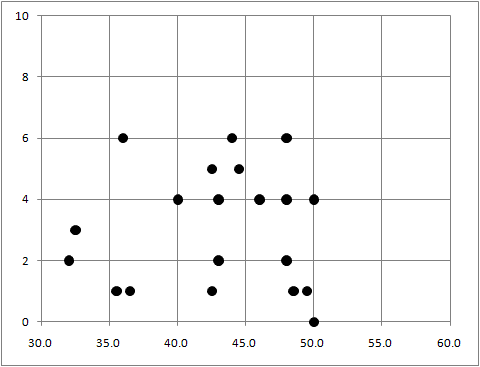 | 差 の 絶 対 値 |  |
| 平均値 | 平均値 | ||
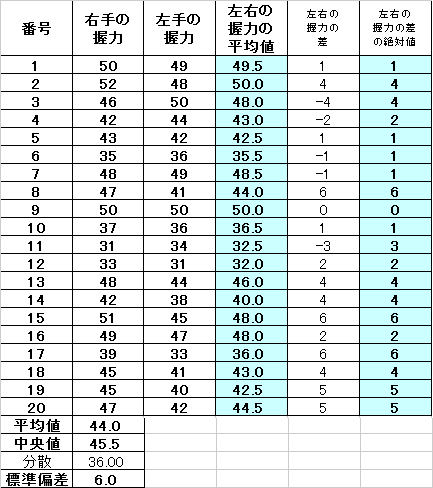
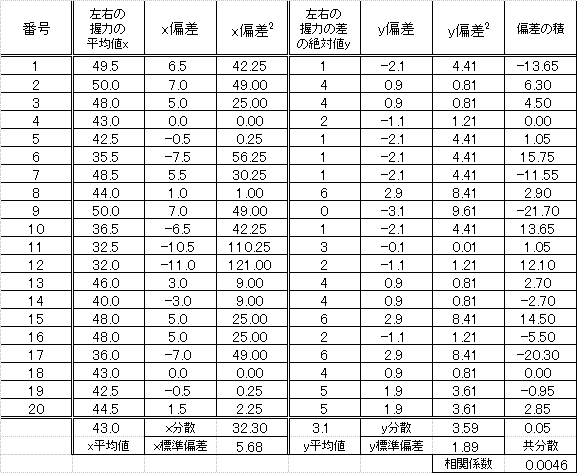
| 「相関係数」 |
| 「共分散」を、それぞれの「分散」の平方根、すなわち「標準偏差」の積で、割ったもの かならず-1と1の間の値であり、
|
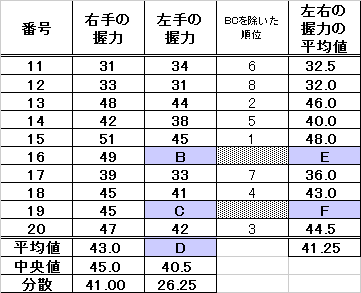
| 「中央値」 |
データを「得点」の高い順(降順)、または、低い順(昇順)に並べたとき、「中央」に来る値。
|

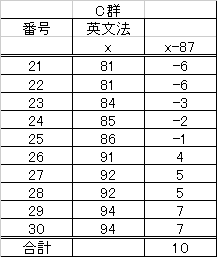
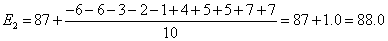
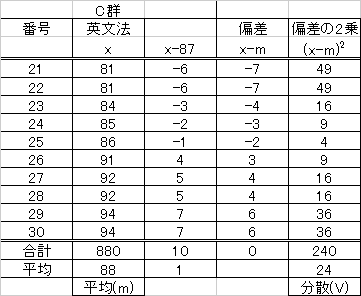
| 「分散」 |
|
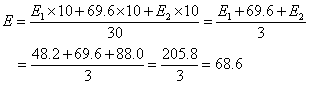

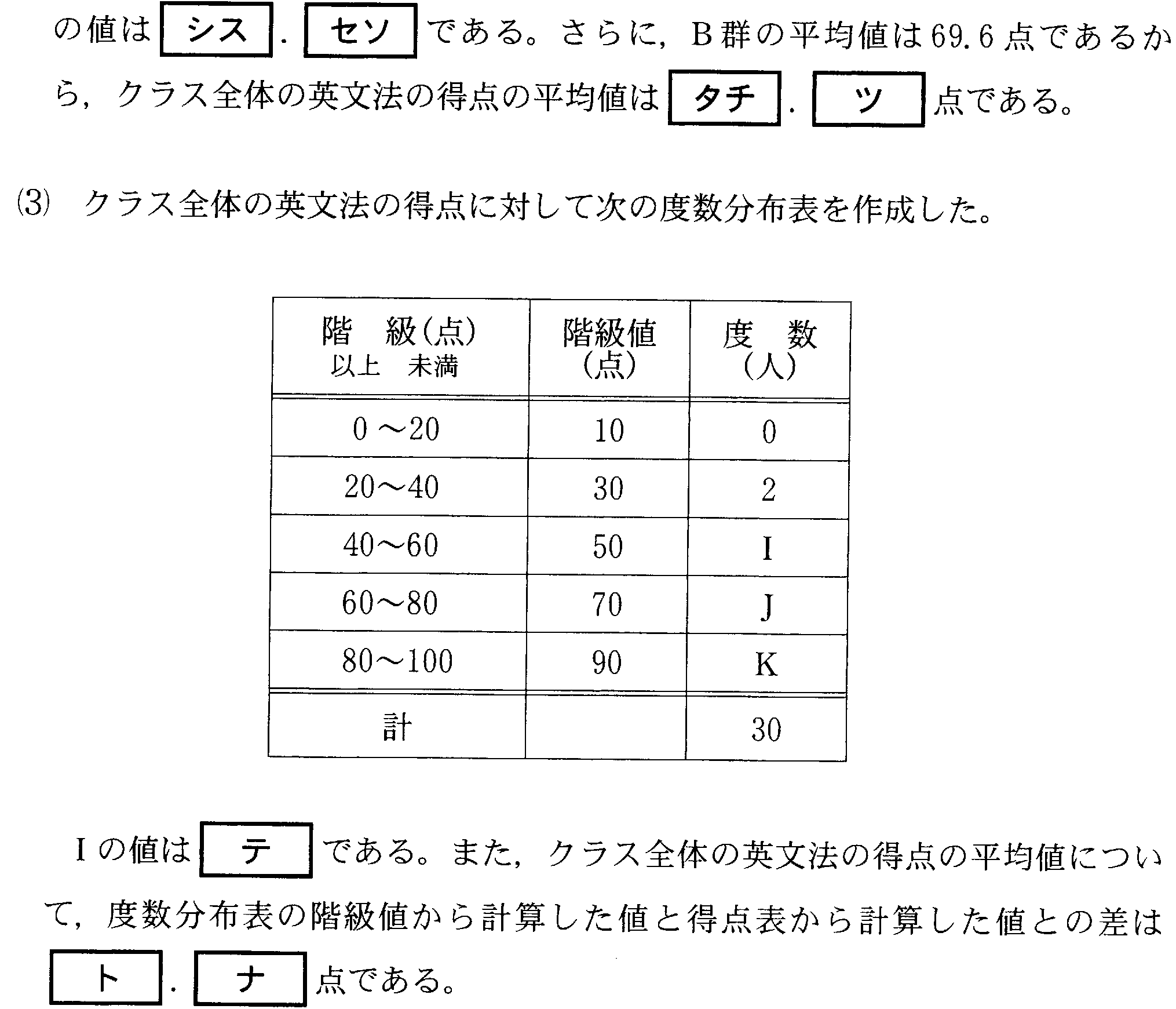
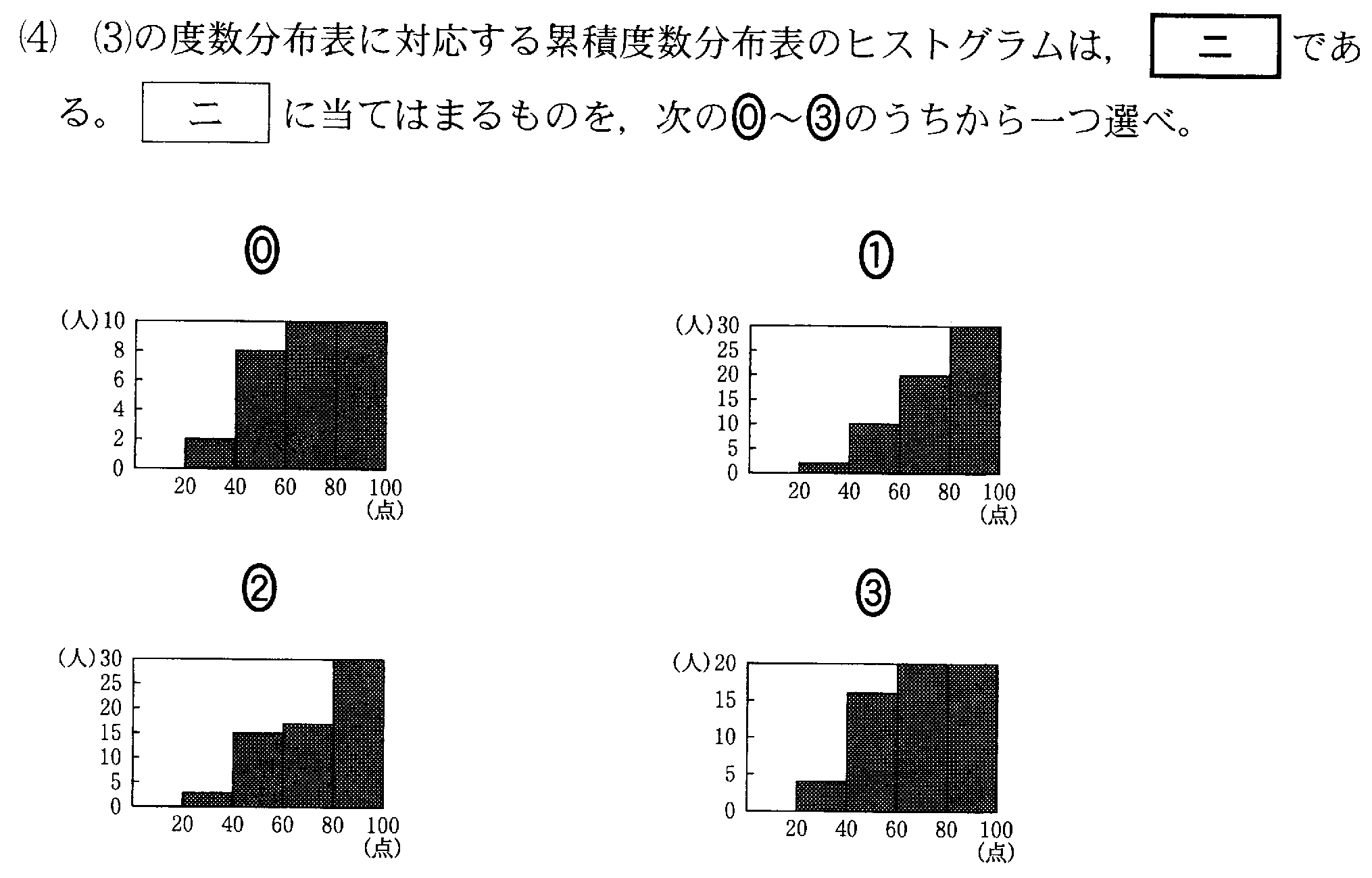
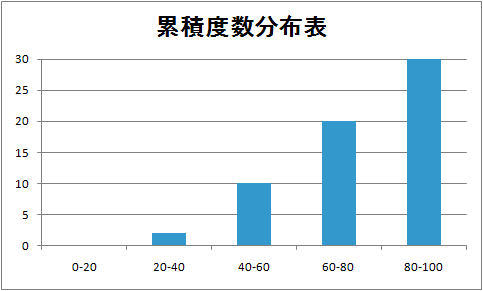
| 「累積度数」の計算方法 | ||
| 階級 | 度数 | 累積度数 |
| 0-20 | 0 | 度数をそのまま0 |
| 20-40 | 2 | 0+2=2 |
| 40-60 | 8 | 2+8=10 |
| 60-80 | 10 | 10+10=20 |
| 80-100 | 10 | 20+10=30 |

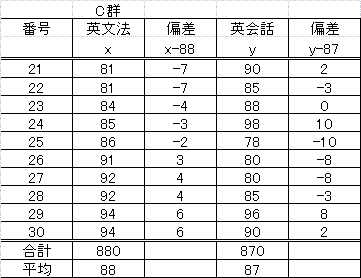
| 解答 | 練習用 | ||
| 英 会 話 | 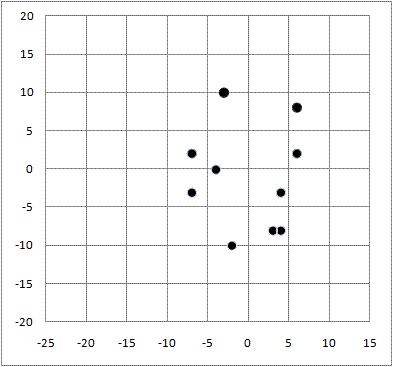 |
英 会 話 |  |
| 英文法 | 英文法 | ||
| 解答 | 練習用 | ||
| 英 会 話 | 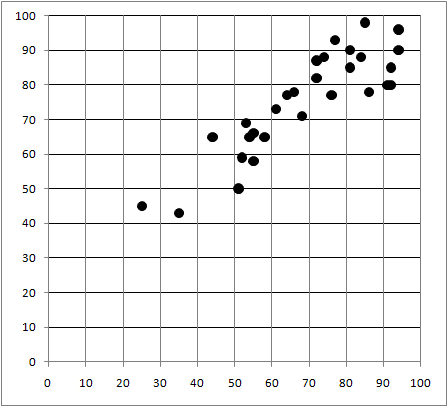 |
英 会 話 |  |
| 英文法 | 英文法 | ||
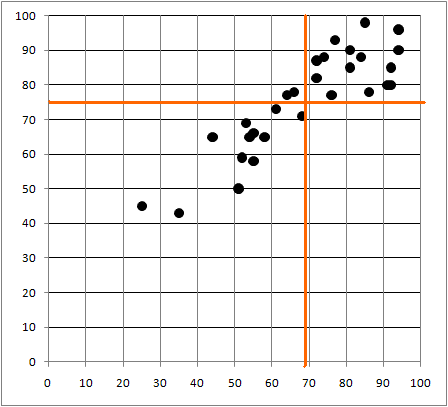
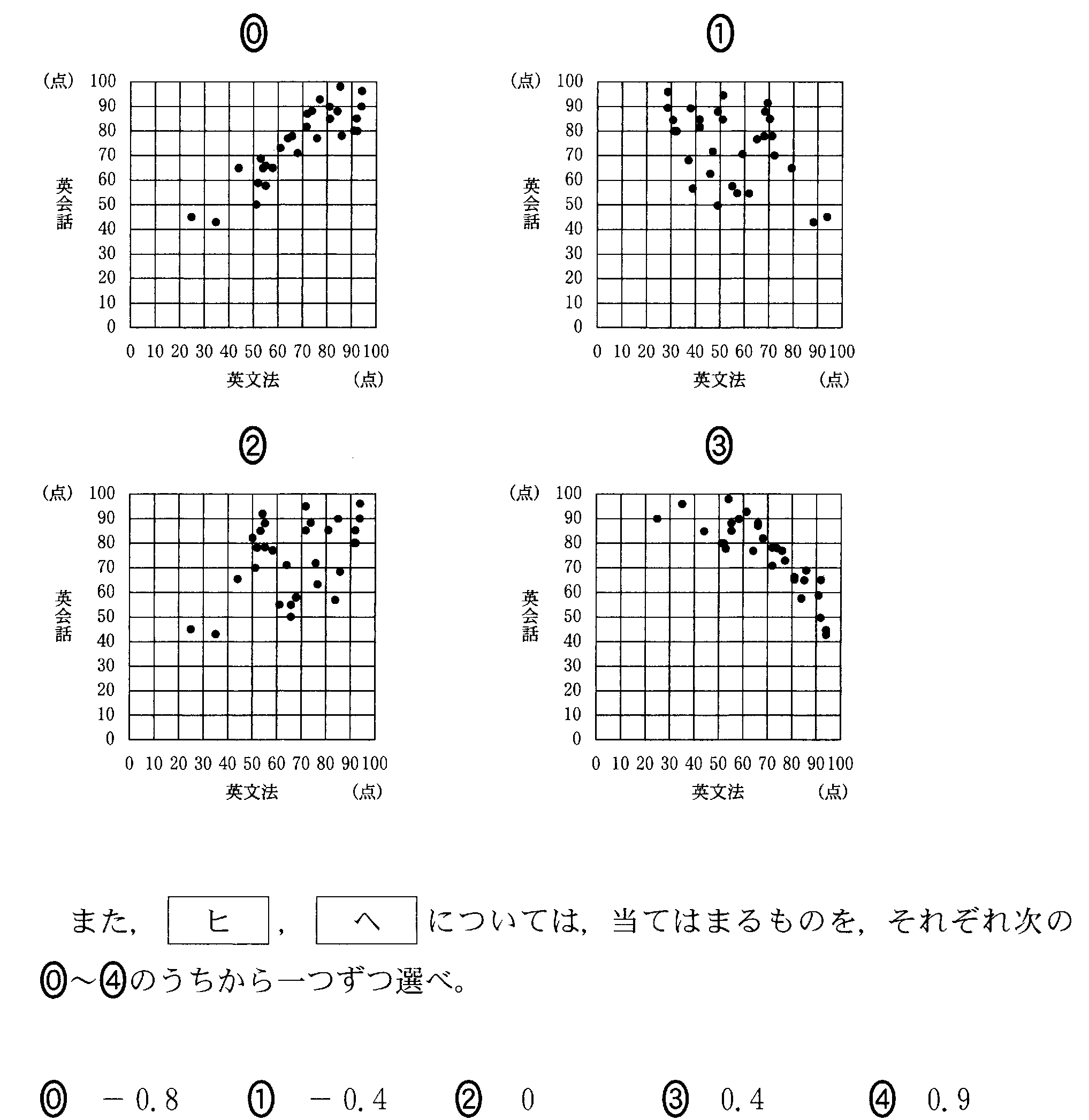
| 「相関係数」 |
| 「共分散」を、それぞれの「分散」の平方根、すなわち「標準偏差」の積で、割ったもの かならず-1と1の間の値であり、
|