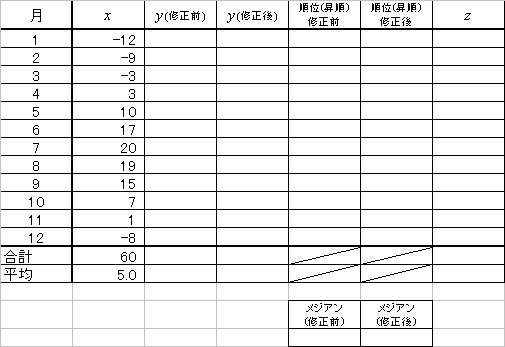
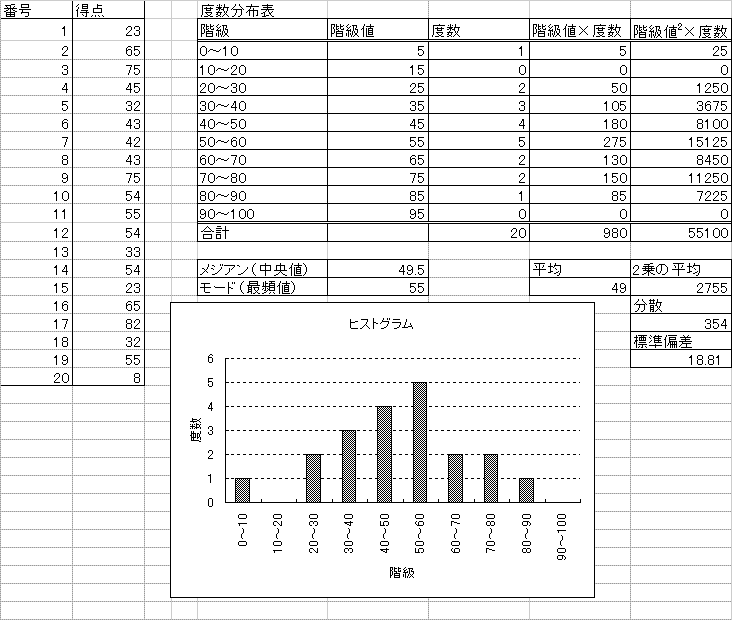
「分布の広がり」を示す指標。
たとえば、平均点が60点のテストで、あなたが70点を取ったとしよう。それは確かに「偉い!」ことに違いない。でも、その「偉さ」は、他の受験者の点の取り方、すなわち点数の「分布」によって異なる。
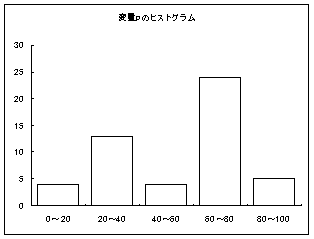
左のグラフのように、平均点の周りに大多数の受験者が集まっているような分布では、平均点より「10点も」上回ったあなたは、「とても・偉い」。
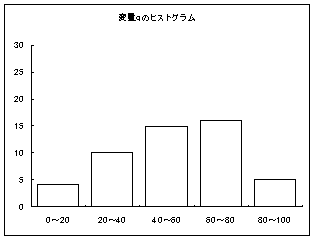
しかし、右のグラフのように、同じ平均点でも0点から100点までなだらかな勾配で広がっているような分布だったら、平均点より、「10点くらい」上回っている人はざらにいるのだから、「そんなに・偉くない」ことになる。
したがって、あなたの「偉さ」を評価するには、「平均点」以外に、このような「分布の広がり」を示す指標が必要だ。
それぞれの受験者の得点が、平均点とどれほど隔たっているか(「偏差」)、その絶対値の合計が大きいほど、「分布の広がり」は大きい、といえる。
「分散」・「標準偏差」は、このようにして考案された。
| 分散・標準偏差 | |
| 小さい | 大きい |
| 平均値の周りに多くのデータが密集した、「シャープな」分布 | 平均値から離れたところにも多くのデータが存在する、「ゆるやかな」分布 |
| 分散 | 定義式 | 実用式 |
| 「偏差」の「2乗」の「平均」 | 「2乗の平均」-「平均の2乗」 | |
| 標準偏差 | 「分散」の正の「平方根」 | |
2つの変量の、「関係の傾向」と「関係の強さ」を同時に示す指標。
たとえばある特定の100人の人間を対象として調査をしたとしよう。この100人のことを「標本(サンプル)」という。個々の「人」には、当然さまざまに異なる性質(属性)があるのだが、「人」と「人」を比較するには、その「属性」が、「数値化」されていなければならない。「よい人」、「悪い人」というのも結構だが、「どのくらい」よいのか悪いのかが示されなければ、少なくとも、比較はできない。
さて、このようにして「数値化」された「属性」、たとえば、「年齢」、「身長」、「体重」、「体脂肪率」、「年収」、「資産額」、、「腕立て伏せの回数」、「国語の点数」、「数学の点数」、などのうち、たった二つのものの「関係」を調べたいとしよう。
「二つ」であるのはもちろん理由がある。私たちは「3次元空間」に生きていると信じているが、実際は、その3次元の外的空間を、網膜という2次元平面に投影した図象として把握している。したがって、人間は物事の「関係」や「傾向」について、原則として2個の「属性」間の関係しか、捉えることができない。
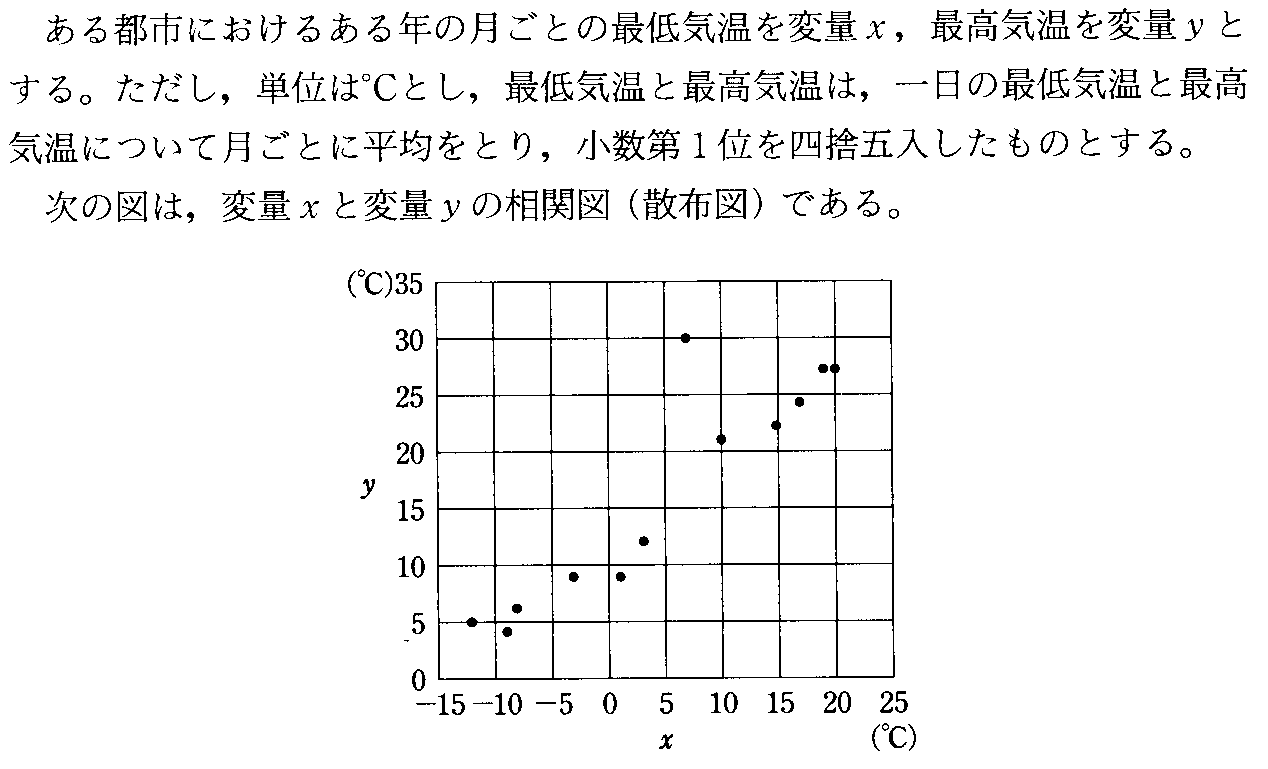
このようにして選ばれ、数値化された2個の「属性」をそれぞれ「変量x」、「変量y」と呼ぼう。この調査結果を、xy平面上にプロットしてみると、一人ひとりのサンプルはそれぞれ「変量x」、「変量y」の値を持つから、点(x,y)に対応する。こうして、xy平面上にサンプルの個数100個分の点が打たれた図面が出来上がる。これを「散布図」、「相関図」などと呼ぶ。
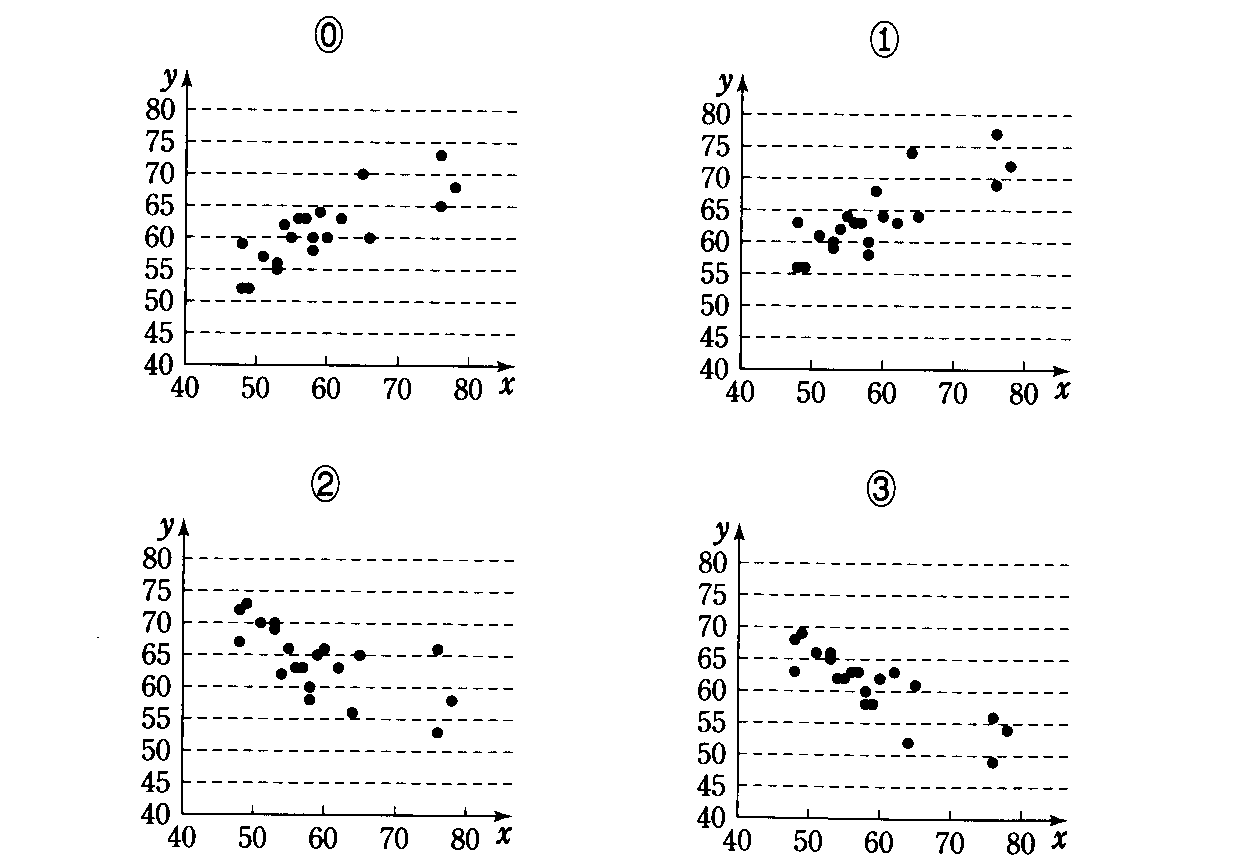
散布図の上に並んだ点のかたまりが、おおよそどのような形をしているかによって、2つの変量の「関係の傾向」および「関係の強さ」を見ることができる。
残念ながら人間はそれほど精度の高い分析機械ではないから、「傾向」と言ったって、もっとも単純な直線関係(比例関係)しか見て取ることができない。
|
| 正の相関 | 負の相関 | 無相関 |
次に「相関の強さ」について考える。サンプルを表す点が、仮に同じ傾きの直線を中心に集まっていたとしても、「集まり方の度合い」によって評価は異なってくる。
多くの点が、直線の周りに密集して集まっていたならは、2つの変量xyの間の直線関係は、より明瞭なものだといえるだろう。
しかし、同じ直線が引けたとしても、多くの点がまばらに集まっているに過ぎないならば、2つの変量xyの間の直線関係は、かなりあいまいなものだとしか言えない。
これが、「相関の強さ」の問題である。
後から詳しく説明するように、「すべての点から最も近い直線(回帰直線)」を、「最小2乗法」と呼ばれる数学的手法で、必ず求めることができる。回帰直線の傾き(回帰係数)の正負が、「相関の正負」を決める。
次に求められた直線(回帰直線)と、各点の間の距離の合計の数値から、「相関の強さ」が決められる。
これら二つの要素を、ひとつの数値で表現しているのが、「相関係数」である。
| 相関係数 -1≦r≦1 | ||
| -1≦r<0 | r=0 | 0<r≦1 |
|
相関がない |
|
|
|
|
| 強い『正』の相関 相関係数 0.81 |
弱い『正』の相関 相関係数 0.41 |
|
|
|
| 強い『負』の相関 相関係数 -0.82 |
弱い『負』の相関 相関係数 -0.43 |
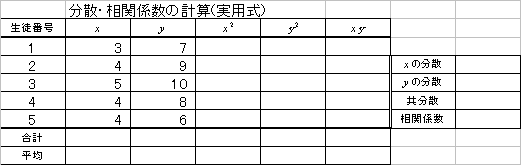
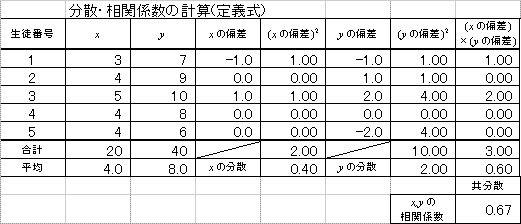
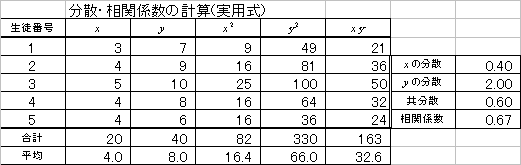
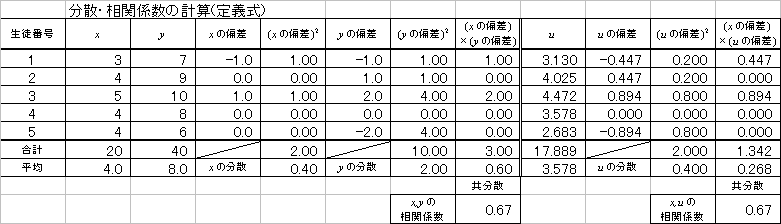
| 共分散 | 定義式 | 実用式 |
| 「偏差」の「積」の「平均」 | 「積の平均」-「平均の積」 | |
| 相関係数 | 「共分散」÷「標準偏差の積」 | |
変量xiの代わりに、次のようにxiの1次式で表される新たな変量uiを考える。
この新たな変量uiについて、その平均、分散、標準偏差を定義に従って計算してみると、
- 平均:
- 分散:
- 標準偏差:
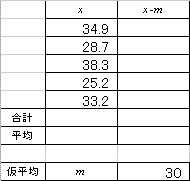
全データから、一律、定数mを引くという、変数変換を行うと、
|
全データを、一律、定数dで割るという、変数変換を行うと、
|
xのデータを、一律、定数d1で割り、yのデータを、一律、定数d2で割り、るという、変数変換を行うと、
|






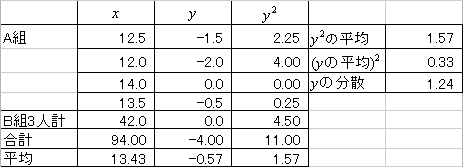
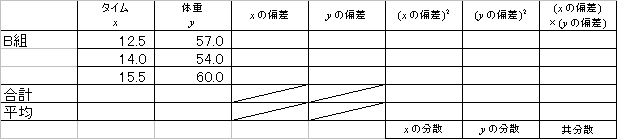
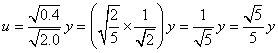 (エオ)
(エオ)
 (カキク)(ケコサ)
(カキク)(ケコサ)

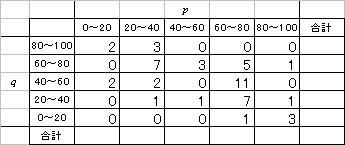
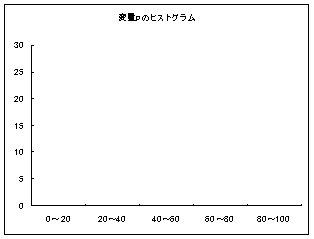
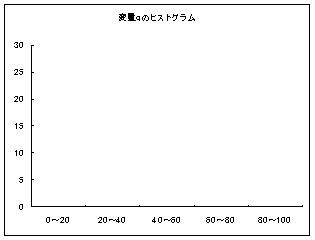
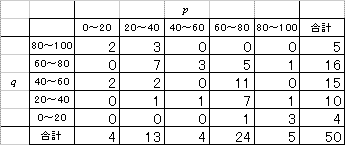

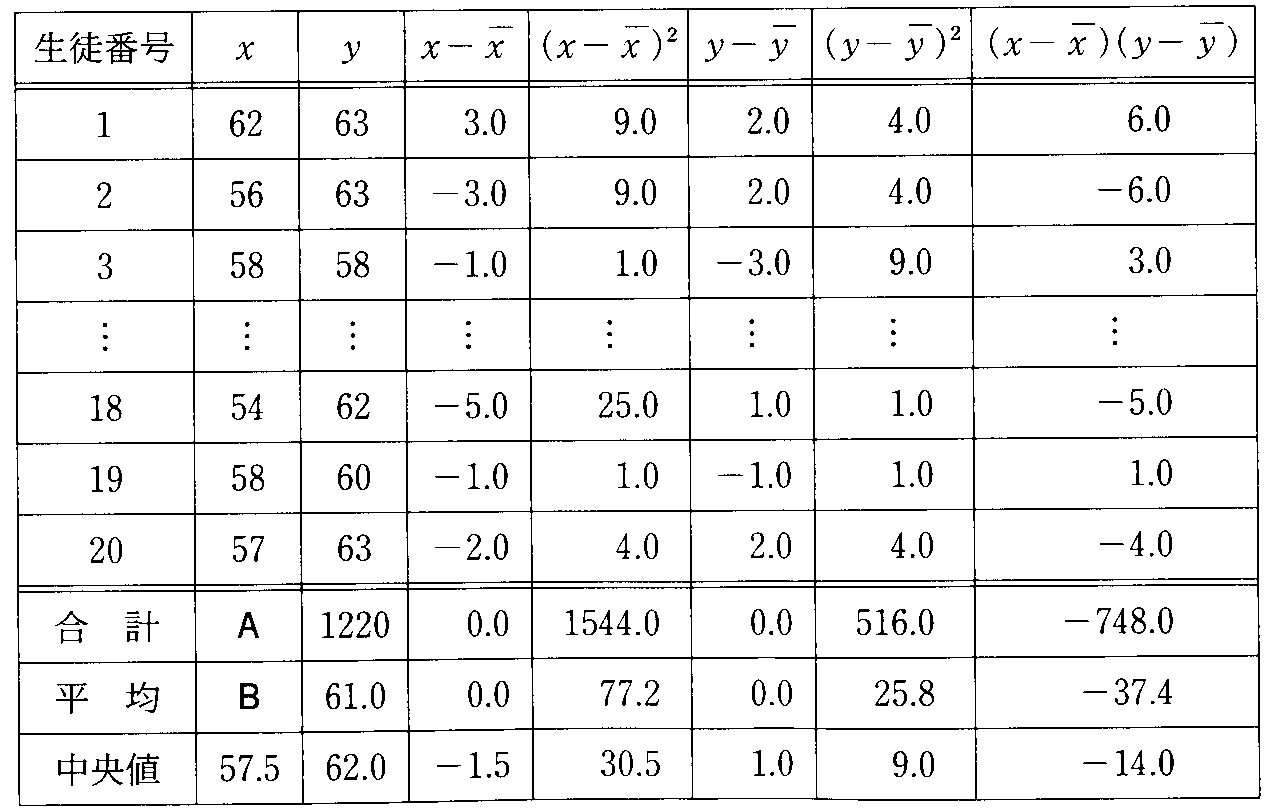






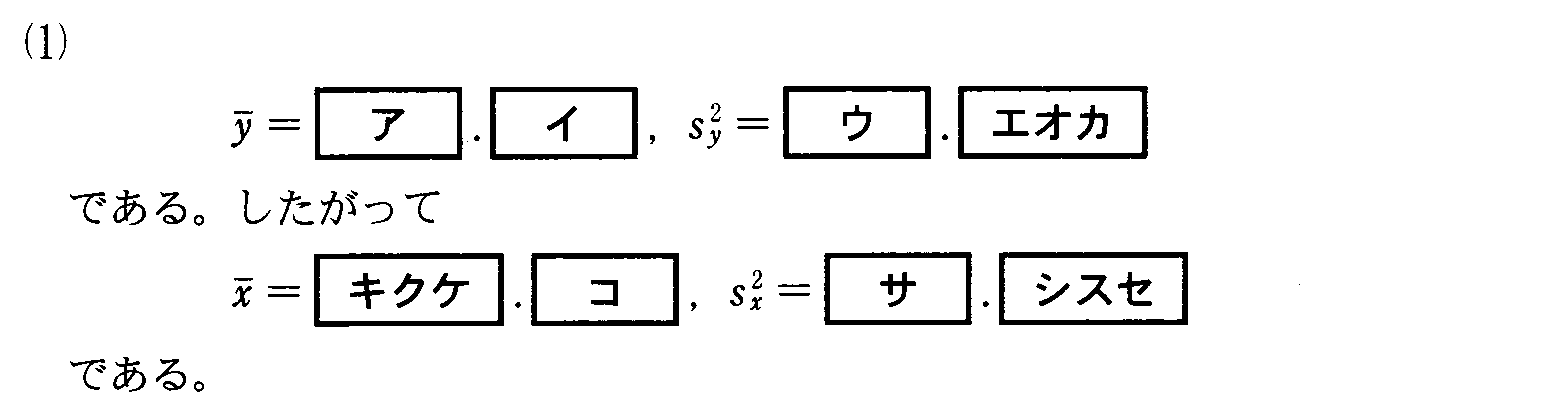



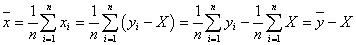
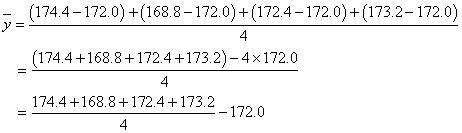

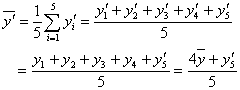
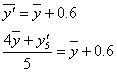
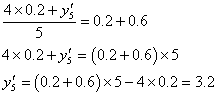
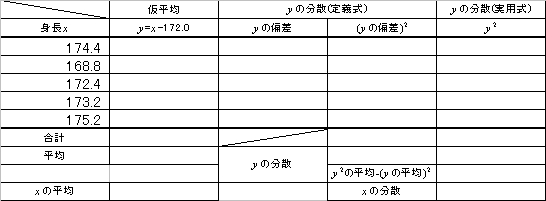

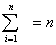 であることを思い出してください。「上手に仮平均を選んだら、たまたま当たっていた」という場合です。
であることを思い出してください。「上手に仮平均を選んだら、たまたま当たっていた」という場合です。
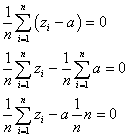
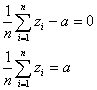
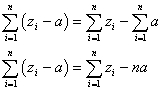


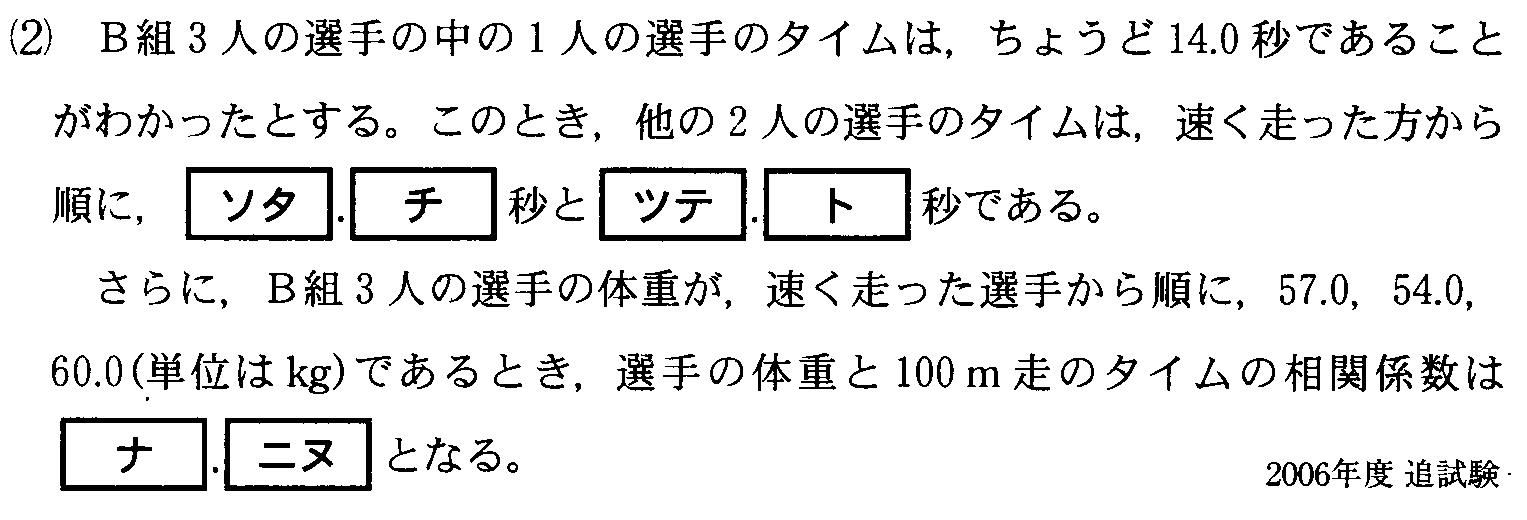




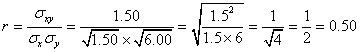


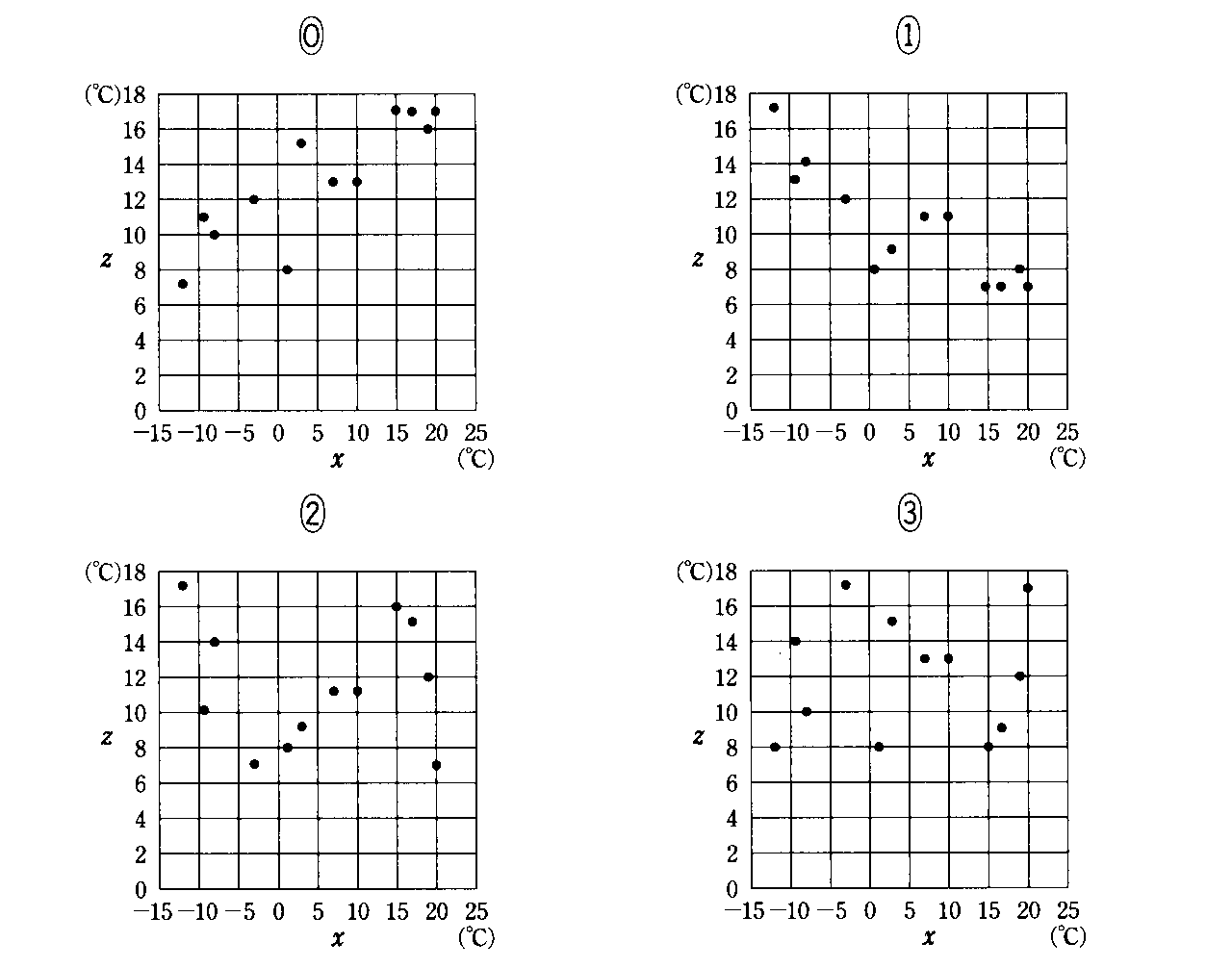

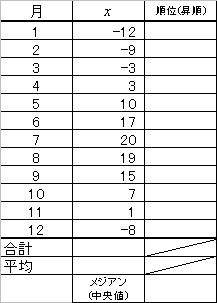
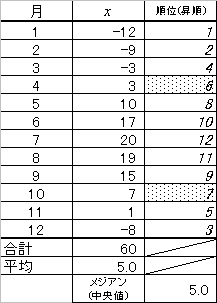


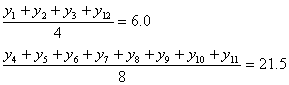
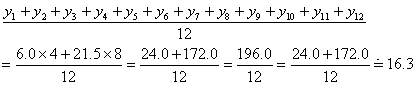 16.3(サシス)
16.3(サシス)