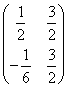横に並んだ成分を「行(row)」、縦に並んだ成分を「列(colum)」と呼ぶ
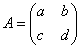
- 加法・減法
対応する成分同士の加減
- 乗法
左側の行列の「行ベクトル」と、右側の行列の「列ベクトル」との「内積」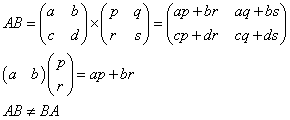
行列の乗法には一般に「交換法則」が成り立たない- A,Bのいずれかが、単位行列の定数倍、もしくは零行列のときは、乗法に関する交換法則が成り立つ。AE=EA=A,AO=OA=O
- Aが単位行列の定数倍でないとき、乗法に関する交換法則AB=BAが成立するための必要十分条件は、B=uA+vEとかけることである。[補1]
- 零行列
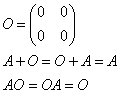
- 単位行列
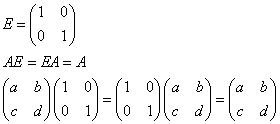
- 逆行列の定義
AB=BA=EをみたすBが「存在するとき」、これをAの「逆行列」と呼び、「A-1」とかく。
AB=Eの場合について、計算経過を示す。BA=Eについても同様である。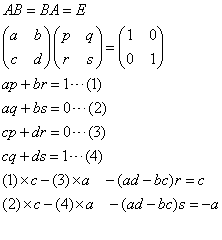
ここで、ad-bcが0でないとすると、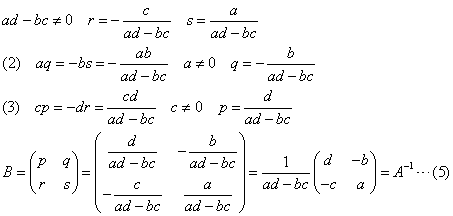
このようにしてAの逆行列が求められた。ちなみに、割り算の過程で、aが0でないこと、またはcが0でないことを仮定したが、それぞれが0の場合も以下のように求められ、その結果は上の(5)式に含まれる。a,cがともに0である場合はad-bcが0でないことに反する。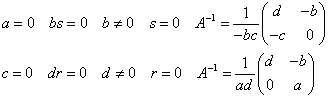
ここからわかるように、ad-bcが0でないときのみ、逆行列が計算できる。
のちに示すように、Aが逆行列を持つ「必要十分条件」はad-bcが0でないことである。
- 逆行列を持つ行列(正則行列)と逆行列を持たない行列(非正則行列)
このように、ad-bcは、ある行列が逆行列をもつか否かの「判別式」として機能する。これを「行列式」と呼び、|A|、detAと書いたりする。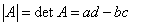
逆行列をもつ行列、すなわちad-bcが0でない行列を、「正則行列」、逆行列をもたない行列、すなわちad-bcが0である行列を、「非正則行列」と呼ぶ。
ここで、ad-bc=0でない、ということを、もう少し別の観点から考える。
- ベクトルの「1次独立性」(2次元・平面ベクトル)
- 互いに平行でなく、
- いずれも0ベクトルでない、
すなわち、以下の式で、平面上の任意の点Pに対して、uとvはかならず一組だけ存在する。平面上の任意の点を表す位置ベクトルは、2個の1次独立なベクトルの「1次結合(線形結合):定数倍と加法のみであらわされる形式」で、ただ一通りに(一意的に)表現できる。 
「独立」とは、互いに他を自分の定数倍で表現できない、という意味であり、1次独立でないことを「1次従属」と呼ぶ。1次従属とは、- 互いに平行であるか、または、
- いずれかが0ベクトルである
- ad-bc=0でない、ということは、列ベクトル(a,c)と列ベクトル(b,d)が「1次独立である」ということと同値(必要十分条件の関係)である。
- 「十分条件」:ad-bc=0でないならば、列ベクトル(a,c)と列ベクトル(b,d)は1次独立である。
「対偶」:列ベクトル(a,c)と列ベクトル(b,d)は1次従属であるならば、ad-bc=0である。
- 「必要条件」:列ベクトル(a,c)と列ベクトル(b,d)が1次独立であるならば、ad-bc=0でない。
「対偶」:ad-bc=0であるならば、列ベクトル(a,c)と列ベクトル(b,d)は1次従属である。
- 「十分条件」:ad-bc=0でないならば、列ベクトル(a,c)と列ベクトル(b,d)は1次独立である。
- Aが逆行列を持つ「必要十分条件」はad-bcが0でない、すなわち、Aの列ベクトル(a,c)と列ベクトル(b,d)は1次独立であることである、ことを証明する。
- 「十分条件」:Aが逆行列を持つならば、Aの列ベクトル(a,c)と列ベクトル(b,d)は1次独立である。
「対偶」:Aの列ベクトル(a,c)と列ベクトル(b,d)が1次従属であるならば、Aは逆行列を持たない。
(a,c)が0ベクトルならば、bsとdrがいずれも0であり、かつ、brとdsがいずれも0でない、という矛盾に陥る。従ってAB=EをみたすBは存在しない。BA=Eについても同様。また(b,d)が0ベクトルの場合も同様。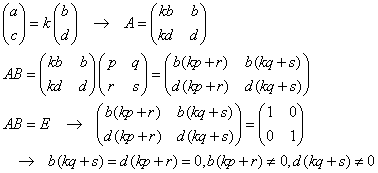
(a,c)が(b,d)の定数倍で表されるならば、やはり矛盾に陥る。従ってAB=EをみたすBは存在しない。BA=Eについても同様。
- 「必要条件」:Aの列ベクトル(a,c)と列ベクトル(b,d)が1次独立であるならば、Aは逆行列を持つ。
Aの列ベクトル(a,c)と列ベクトル(b,d)が1次独立であるならば、ad-bc=0でない。
ad-bc=0でないならば、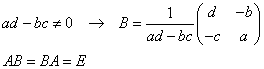
でしめされる、BがAB=BA=Eをみたすので、Aの逆行列である。
Aが逆行列を持つ「必要十分条件」はad-bcが0でない、すなわち、Aの列ベクトル(a,c)と列ベクトル(b,d)は1次独立であることである。
行ベクトルについても、同様なことがいえる。Aが逆行列を持つ「必要十分条件」はad-bcが0でない、すなわち、Aの行ベクトル(a,b)と行ベクトル(c,d)は1次独立であることである。 - 「十分条件」:Aが逆行列を持つならば、Aの列ベクトル(a,c)と列ベクトル(b,d)は1次独立である。
- ベクトルの「1次独立性」(2次元・平面ベクトル)
- ハミルトン・ケーリーの定理
任意の行列に対して、次の式が成立する。
A2-(a+d)A+(ad-bc)E=O
左辺の第3項の係数は、すでに見た「行列式」|A|、detAである。左辺の第2項の係数(a+d)は行列の「対角成分(左上から右下に向かって並ぶ成分)」の和であり、trace(A)などと呼ばれる。
ハミルトン・ケーリー式は行列の2次式であるから、行列の次数を下げる機能をもつ。
A2 = (a+d)A-(ad-bc)E 左辺・2次式 右辺・1次式
- ハミルトン・ケーリーの定理の証明
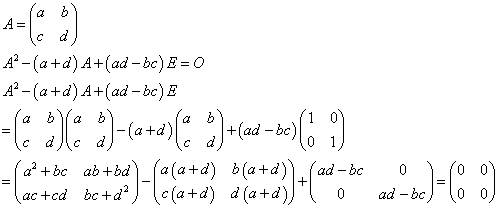
- では、ある行列について成立する2次式は、ハミルトン・ケーリー式だけなのだろうか?

行列Aについて(1)式が成立するとする。ハミルトン・ケーリーの定理から、(2)式が成立する。両式からAの二乗の項を消去すると、(3)式が得られる。
左辺の係数p+(a+d)が0ならば、左辺は零行列である。右辺は単位行列の定数倍であるから、これが零行列となるためには、右辺の係数q-(ad-bc)も0でなければならない。このとき、(1)式はハミルトン・ケーリー式に一致する。
では、p+(a+d)が0でないならば、どうであろうか?(3)式より、Aは単位行列の定数倍となるから、b=c=0,a=dである。各成分を比較すると、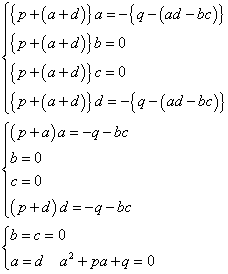
つまり、行列Aについて式(1):A2+pA+qE=Oが成立するとき、
この式の行列Aを変数xで置き換えた方程式:x2+px+q=Oの解に対して、
行列A=xEは、かならず式(1)を満たす。
別の見方をすると、Aが単位行列の定数倍、A=xEで表されるとき、
xを解とする2次方程式:x2+px+q=0は無数に存在する。 これらのp,qに対して、無数の式(1)が存在する。
[例題1] 次の式を満たす行列Aを求めよ。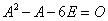
- [十分条件]:Aが逆行列を持つならば、ad-bcは0でない。
「背理法」(後述)によって証明する。
Aが逆行列を持ち、かつad-bc=0であると仮定すると、矛盾にいたることを示す。
ハミルトン・ケーリーの定理から、ad-bc=0のとき、
A2-(a+d)A=O
A2=(a+d)A
Aは、逆行列A-1をもつから、これを両辺に左からかけると、
A-1A2=(a+d)A-1A
A=(a+d)E
ここで、a+d≠0とすると、Aは単位行列の定数倍であるから、ad-bc=0に反する。
また、a+d=0とすると、Aは零行列であるから、逆行列を持つことに反する。
こうして、いずれの場合も矛盾を生じ、Aが逆行列を持ち、かつad-bc=0であることがありえないことが示された。
よって、Aが逆行列を持つならば、ad-bcは0でない。
- [必要条件]:ad-bcが0でないならば、Aは逆行列を持つ。
ad-bc=0でないならば、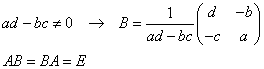
でしめされる、BがAB=BA=Eをみたすので、Aの逆行列である。
積が零行列であるのに、それぞれ零行列ではない二つの行列を、相互に「零因子」と呼ぶ。
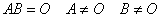
- 「零因子は逆行列を持たない」ことを証明する。
- 「背理法」による証明
「Aであるならば、Bである」ことを証明する代わりに、「Aであり、かつBでないことを仮定すると、矛盾を生じる」ことを証明する方法。AならばBである ←→ AはBであるための十分条件である ←→ 
←→ 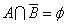
集合Aが集合Bに「包含」されているとき、
「A」と「Bの補集合」は共通部分を持たない
←→ 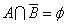
- 「行列A,Bが零因子であるならば、A,Bはともに逆行列を持たない。」
[背理法]「行列A,Bが零因子であり、かつ、A,Bのいずれかが逆行列を持つと仮定すると、矛盾を生じる。」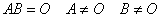
であり、かつAが逆行列を持つと仮定する。Aの逆行列A-1が存在するのであるから、これをAB=Oの両辺に左からかけると、
B=Oとなり、仮定に反する。また、Bが逆行列を持つと仮定する。Bの逆行列B-1が存在するのであるから、これをAB=Oの両辺に右からかけると、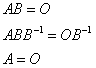
B=Oとなり、仮定に反する。
こうして、いずれの場合も矛盾に陥った。矛盾に陥った原因は、「A,Bのいずれかが逆行列を持つ」と仮定したことにあるから、「A,Bはともに逆行列を持たない」ことが証明された。
- 「背理法」による証明
- 零因子は、どのような行列であろうか?
行列の積は、左側の行列の「行ベクトル」と右側の行列の「列ベクトル」との「内積」を各要素とするから、AB=Oならば、次のように書ける。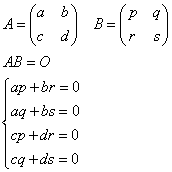
これは、ベクトル(a,b)と(p,r)、(a,b)と(q,s)、(c,d)と(p,r)、(c,d)と(q,s)が、それぞれ「直交」していることを意味する。
であるならば、ベクトル(a,b)と(c,d)、(p,r)と(q,s)は、それぞれ「平行」でなければならない。
このことからも、Aの行ベクトル(a,b)と(c,d)、Bの列ベクトル(p,r)と(q,s)、はそれぞれ1次従属である、従って、A,Bはいずれも逆行列を持たないといえる。
そこで、(c,d)が(a,b)の定数倍、(q,s)が(p,r)の定数倍として以下のように書けば、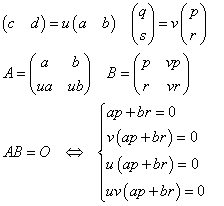
となり、与えられた行列A(任意のa,b,u、ただし、a,bは同時に0ではない)に対して、AB=0を満たす行列Bは、p,rはap+br=0を満たす任意の数であり、vはまったくの任意の数、として定められることがわかる。[補2]
ちなみに、a,bがともに0であれば、Aは零行列であり、任意の行列Bに対してAB=0が成立する。もちろん、これらは零因子ではない。
[例題2] 次の行列Aに対して、AB=Oを満たす行列Bを求めよ。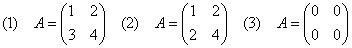
- 行列の2次式が、以下のように因数分解されたとしよう。「解と係数の関係」より以下のようにいえる。
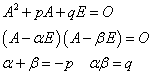
- (A-αE)が零行列ならば、(A-βE)は任意であり、A=αEである。
- (A-βE)が零行列ならば、(A-αE)は任意であり、A=βEである。
- Aが単位行列Eの定数倍でないとき、(A-αE)、(A-βE)はいずれも零行列でない。このとき、この2次式は「ハミルトン・ケーリー式」に一致する。
また、このとき、(A-αE)と(A-βE)は相互に零因子である。
Aはa+d=-p,ad-bc=qを満たす任意の行列であり、 のちに述べるように、これらは、α,βを「固有値」とする行列である。
[例題3] 次の式を満たす行列Aを求めよ。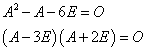
それ自身は零行列ではないにもかかわらず、n乗すると零行列になる行列を「ベキ(冪)零行列」という。「冪乗」とは、「累乗」、n乗のことである。

- 「ベキ零行列は逆行列をもたない」ことを証明する。
[背理法]「Aがベキ零行列であり、かつ逆行列をもつと仮定すると、矛盾を生じる。」
Aに逆行列が存在するならば、これを両辺に左から(右からでも)、n回かけて、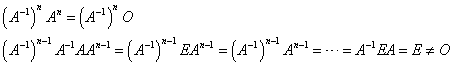
E=Oとなり矛盾を生じた。従って、Aがベキ零行列であるならば、Aは逆行列を持たない。
- 「Aのn乗が零行列ならば、Aの2乗が零行列である」ことを証明する。
- Aが零行列であるならば、当然A2=Oである。
- Aが零行列でなく、かつ、An=O、すなわちAが「ベキ零行列」であるとき、「Aがベキ零行列であるならば、Aは逆行列を持たない」から、ad-bc=0である。ハミルトン・ケーリー式より、Aのn乗は以下のようにかける。これが零行列であり、かつ、Aが零行列でないことから、a+d=0となり、再びハミルトン・ケーリー式より、Aの2乗が零行列であることが示される。
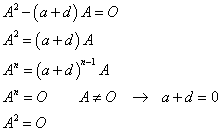
- では、ベキ零行列は、具体的にどんな形をしているのか?
ベキ零行列では、逆行列が存在しないから、列ベクトル同士は1次従属である。
[例題4] ベキ零行列の例を挙げよ。
x,yを未知数とする2元連立1次方程式は、行列を用いて以下のように書ける。
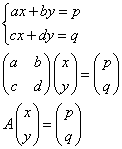
- Aが逆行列を持つならば、これを両辺に左からかけると、
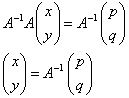
となり、(x,y)はただ一組の解を持つ。
- Aが逆行列を持たないとき、Aの行ベクトル同士は、1次従属であるから、
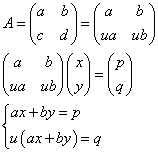
ここで、- p=0ならば、q=0となり、のちに述べる「連立1次『斉次』方程式」の問題となる。
- p=0でなく、q=upならば、
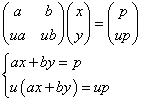
となり、ax+by=pを満たす任意の数が、(x,y)の解となる。
p=0でなく、u=0、従って、q=0のときも同様である。
- p=0でなく、u=0でないuに対して、q=upと表わせないとき、
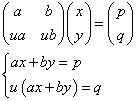
これらを満たす(x,y)の解は存在しない。
- p=0ならば、q=0となり、のちに述べる「連立1次『斉次』方程式」の問題となる。
別の言い方をすると、
- (a,b)と(c,d)が1次独立であるとき、すなわち2式が直線を表し、その「法線ベクトル」(a,b)と(c,d)が、平行でないとき、2直線はただ1点で交わる。
- (a,b)と(c,d)が1次独立でないとき、いずれかが0ベクトルである場合を除き、2式は「平行」または「一致」の関係にある。
- 「一致」の場合、共有点は無数に存在する。
- 「平行」の場合、共有点は存在しない。
[例題5] 次のx,yに関する連立1次方程式を解け。

連立1次方程式において、右辺の列ベクトルが零ベクトルであるようなものを、定数項(0次)を含まない、次数のそろった1次式であることから、「斉1次式」と呼ぶ。
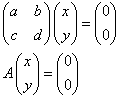
この連立1次方程式において、(x,y)=(0,0)は、明らかに解であるから、これを「自明解」とよぶ。
(x,y)=(0,0)以外の解(これを「非自明解」と呼ぶ)をもつために係数行列Aが満たすべき条件を求める。
- Aが逆行列を持つならば、これを両辺に左からかけると、
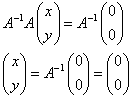
となり、(x,y)はただ一組の解(0,0)を持つことになる。
- Aが逆行列を持たないとき、Aの行ベクトル同士は、1次従属であるから、
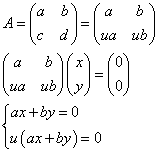
となり、ax+by=0を満たす任意の数が、解となる。この中には、当然(x,y)=(0,0)以外のものも含まれる。
別の見方をすると、これら2式は、(行ベクトルが0ベクトルである場合を除き)いずれも原点を通る直線を表している。したがって、原点は、明らかにこれらの共有点である。
- 2直線の法線ベクトルが、1次独立なら、2直線は平行でないから、交点は原点のみである。
- 2直線の法線ベクトルが平行なら、2直線は一致するから、共有点は無数に存在する。
| 連立1次『斉次』方程式が、(x,y)=(0,0)以外の解(非自明解)を持つための、必要十分条件は、係数行列Aが逆行列を持たない、ことである |
- 固有値
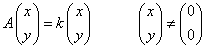
を満たす定数kを行列Aの「固有値」と呼ぶ。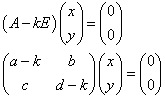
この「連立1次斉次方程式」が、(x,y)=(0,0)以外の解(非自明解)を持つのは、(A-kE)が逆行列を持たないときであるから、
となる。これを行列Aの「固有方程式」と呼び、この2次方程式の解が「固有値」となる。固有方程式の係数は、「ハミルトン・ケーリー式」の係数と同じである。
- 固有ベクトル
固有値をk1,k2(重解の場合も含む)としたとき、
を満たす列ベクトル(x1,y1),(x2,y2)をそれぞれ、k1,k2に対応する「固有ベクトル」と呼ぶ。
- 行列の「対角化」
二つの「固有ベクトル」を横に並べて行列を作れば、
となり、行列Aが、その固有値を「対角成分」にもつ行列(「対角行列」という)と関連付けられたことになる。これを、行列の「対角化」という 。
固有方程式が「重解」を持つとき、k1,k2は等しくなるので、対角行列Bは、単位行列の定数倍となる。
- n乗が簡単に求められる行列
- 零行列
- 単位行列
- 逆行列をもたない行列(非正則行列)
- 対角行列
- 上半三角行列

- 「対角化」によるn乗の計算
行列Aが、異なる二つの固有値k1,k2をもつとき、これらの固有値を対角成分にもつ行列B、それぞれに対応する固有ベクトルを列ベクトルとして横に並べた行列Pとの間に、次のような関係が成立する。

ここから、Pが逆行列を持つときは、以下のようにしてAのn乗が計算できる。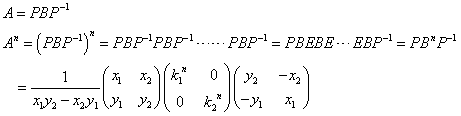
- 「上半三角化」によるn乗の計算
行列Aが固有値を一つしかもたないとき、すなわち、固有方程式が重解を持つとき、一つの固有値に対応する固有ベクトルは、互いに平行(1次従属)にならざるを得ないから、Pは逆行列を持たない。従って、対角化によるn乗はできない。
そこで次のような方法を用いる。行列Aのただ一つの固有値をk、これに対応する固有ベクトルを(x0,y0)とする。
行列Bとして、対角成分にkをとり、これをはさんだ上半分にのみ0以外の要素wがある行列(上半三角行列)を選ぶ。行列Pの右側の列ベクトル(u,v)はAP=PBが成り立つように、適当に決定する。(未知数u,v,wの3個に対し、条件式は2個だけであるから、無数の解が存在する。)
こうして、行列Aが「上半三角行列」Bと関連付けられ、Bのn乗からAのn乗が計算できる。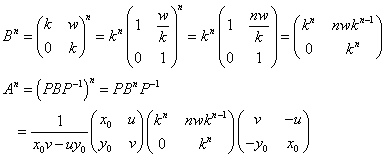
唯一の固有値kが0であればこの方法は用いられないが、固有方程式が0の重解をもつときは、ハミルトン・ケーリー式から、Aの2乗が零行列、すなわちベキ零行列であるから、n乗も零行列である。
[例題6]次の行列のn乗を求めよ。
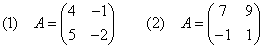
Aが単位行列の定数倍でないとき、乗法に関する交換法則AB=BAが成立するための必要十分条件は、B=uA+vEとかけることである。
- 「十分条件」:AB=BAならば、B=uA+vEをみたすu,vが存在する。
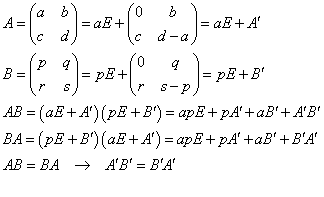
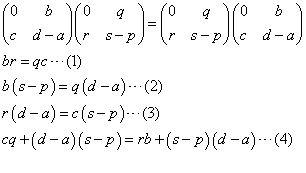
(1)が成立すれば(4)は自明である。(1)に関して、bが0かどうかについて以下のように場合わけして考える。
また、次のようにおく。
- b=0のとき→c=0またはq=0
- b=c=0のとき
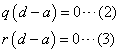
- d=aのとき
A=aEすなわち、Aは単位行列の定数倍であるから、任意のBに対してAB=BAである。 - d=aでないとき

- d=aのとき
- b=q=0のとき
(3)よりr(d-a)=c(s-p)
c=0は上で検討済みだから、c=0でないとする。
- b=c=0のとき
- b=0でないとき
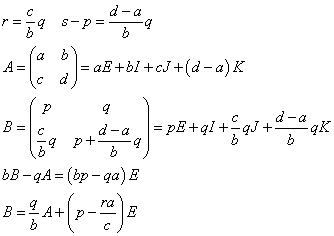
- b=0のとき→c=0またはq=0
- 「必要条件」:B=uA+vEならば、AB=BAである。
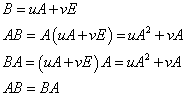
| 乗法に関する交換法則AB=BAが成立するための必要十分条件 | |
| Aが単位行列の定数倍であるとき | 任意のBに対してAB=BAが成立する |
| Aが単位行列の定数倍でないとき | B=uA+vEをみたすu,vが存在する |
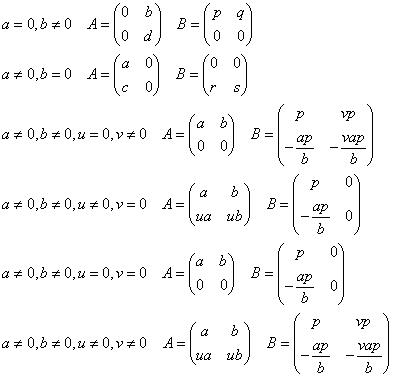
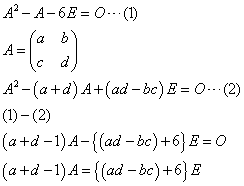
ここで、
- Aが単位行列の定数倍でないとすると、a+d=1であり、左辺は零行列であるから、ad-bc=-6である。
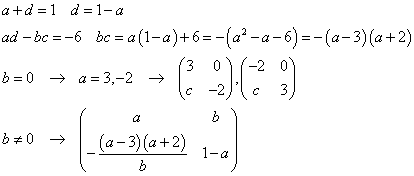
- a+d=1でないとすると、Aは単位行列の定数倍であり、b=c=0かつa=d、すなわちA=aEである。
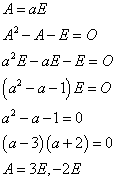
(1)B=O
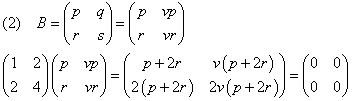
p+2r=0を満たす任意の行列
(3)任意の行列
- (A-3E)が零行列とすると、A=3E
- (A+2E)が零行列とすると、A=-2E
- (A-3E),(A+2E)いずれもが零行列でないとすると、これらは「零因子」
Aはa+d=1,ad-bc=-6を満たす任意の行列である。
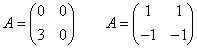
係数行列の「行列式」を求めると、
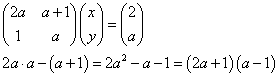
したがって、a=-1/2または、a=1のときこの行列は逆行列をもたない。
逆行列を持たないとき、すなわち、まずa=-1/2のとき、
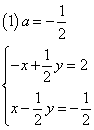
このとき、これら両式を同時に満たす(x,y)は存在しない。
次にa=1のとき、

となり、2式は同値となった。
したがって、(x,y)はx+y=1を満たす任意の数である。
最後に、係数行列が逆行列を持つ場合、以下のようにただ一組の(x,y)が定まる。
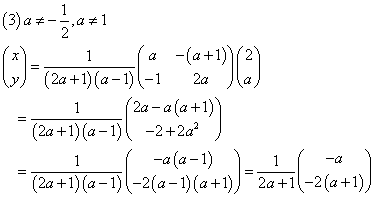
(1)
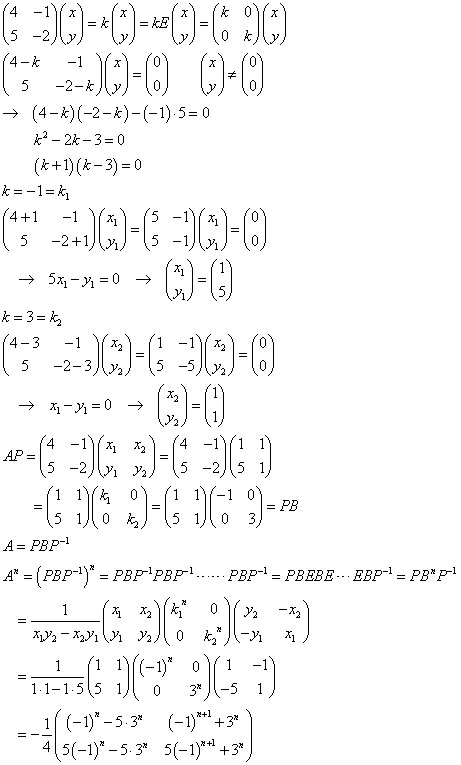
(2)
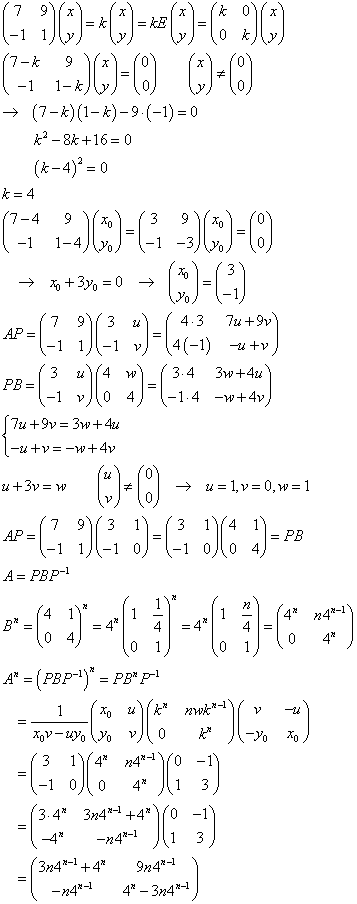


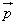 =(x1,y1)、列ベクトル
=(x1,y1)、列ベクトル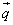 =(x2,y2)をもちいて、
=(x2,y2)をもちいて、
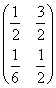
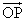 =
=
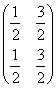
 =A
=A =
= -
-