A= |
a | b |  |
| c | d |
が、逆行列をもつための必要十分条件は、
ad-bc≠0
であることを証明せよ。
- Aが逆行列をもつための必要条件が、ad-bc≠0であること
すなわち、
Aは逆行列をもつならば、ad-bc≠0である
ことを、示す。
- ここに、
｢Aが逆行列をもつ｣
とは、
AB=BA=E・・・@
を充たすような2次の正方行列Bが存在することである。
ただし、Eは単位行列を表し、次のように定義される。
E= 1 0 0 1
- 一方、
2次の正方行列A
に対しては、｢ハミルトン･ケーリーの定理｣と呼ばれる以下の式が成立することが知られている。A= a b c d
A2-(a+d)A+(ad-bc)E=O・・・A
ここに、Oは零行列である。
O= 0 0 0 0
- では、ここで、｢Aが逆行列をもち｣、かつ、｢ad-bc=0｣であると仮定すると、
Aより、
A2=(a+d)A・・・B
となる。一方、@をみたすBが存在するのであるから、これをこのB式の両辺に右側からかけると、
A2B=(a+d)AB
AAB=(a+d)AB
AE=(a+d)E
A=(a+d)E
a b = a+d 0 c d 0 a+d
となり、
a=b=c=d=o
すなわち、A=Oが導かれる。
B式の両辺にBを左側からかけた場合も同様にして、
BA2=(a+d)BA
BAA=(a+d)BA
EA=(a+d)E
A=(a+d)E
となり、やはり A=Oが導かれる。
明らかに、
OB=BO=O
であるから、これは@に反している。このような矛盾が生じた理由は、
｢Aが逆行列をもち｣、かつ、｢ad-bc=0｣であると仮定
したことにあるから、これが誤っている。
こうして、
Aは逆行列をもつならば、ad-bc≠0である
であることが、示された。
- ここに、
｢Aが逆行列をもつ｣
とは、
- Aが逆行列をもつための十分条件が、ad-bc≠0であること
すなわち、
ad-bc≠0であるならば、Aは逆行列をもつ
ことを、示す。
ad-bc≠0であるから、｢ハミルトン･ケーリーの定理｣A式の両辺を
ad-bc
で割ると、
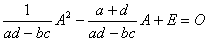
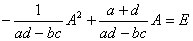
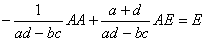
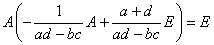
となるから、Bを次のようにおくと、
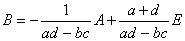
AB=E
となる。また、
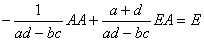
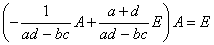
であるから、
BA=E
である。こうして、
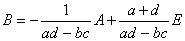
すなわち、
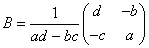
は、Aの逆行列である。
以上から、ad-bc≠0であるならば、Aは逆行列をもつことが示された。
√2が有理数である、すなわち、
√2=m/n・・・@
をみたす、互いに素な整数m,nが存在する、と仮定する。
@の両辺を2乗すると、
2=m2/n2
2n2=m2・・・A
となるから、mは2を因数に持つことになる。
そこで、整数m'を用いて、
m=2m'・・・B
と表すことにすると、ABより、
2n2=4m'2
n2=2m'2
となるから、nは2を因数に持つことになる。
m,nともに2を因数に持つことになり、
これは、｢@をみたす、互いに素な整数m,nが存在する｣との仮定に矛盾している。
こうして、@をみたす、互いに素な整数m,nは存在しないこと、すなわち、√2は無理数であることが示された。