





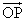 =(x1,y1,z1)
=(x1,y1,z1)
 =(x1,y1,z1)
=(x1,y1,z1)
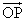 =x1i+y1j+z1k
=x1i+y1j+z1k
 =x2i+y2j+z2k
=x2i+y2j+z2k
|
ベクトルの「外積(ベクトル積)」は a×b=|a||b|sinθ・n ただし、nは、次にように定義される。 aをbに重なるように、同一平面内で最短距離で、つまりπ以下の角度で、回転させたとき、 これを「右ねじ」に見立てると、それが進む方向の単位ベクトル。 θはa,bのなす角のうち、小さい方、すなわち、π以下の角度。 |
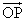 ×
× =(x1i+y1j+z1k)×(x2i+y2j+z2k)
=(x1i+y1j+z1k)×(x2i+y2j+z2k)
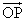 ,
, のいずれとも垂直であればよい。
のいずれとも垂直であればよい。
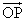 =0
=0
 =0
=0
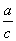 +y1
+y1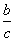 +z1=0
+z1=0
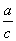 +y2
+y2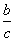 +z2=0
+z2=0
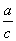 =s ,
=s , 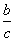 =t とおけば、
=t とおけば、
 |
x1 | y1 |  |
 |
s |  |
= |
-z1 |  |
| x2 | y2 | t | -z2 |
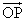 と
と は「1次独立」であるから、通・常・、
は「1次独立」であるから、通・常・、
| 1 |  |
y2 | -y1 |  |
 |
-z1 |  |
= |
s |  |
 |
x1y2-y1x2 | -x2 | x1 | -z2 | t |
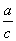 =(y1z2-z1y2)/(x1y2-y1x2)
=(y1z2-z1y2)/(x1y2-y1x2)
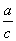 =(z1x2-x1z2)/(x1y2-y1x2)
=(z1x2-x1z2)/(x1y2-y1x2)
| 三角形の面積 |
|
△ABCの面積をS、∠BAC=θとすると、
S= 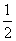 AB・ACsinθ AB・ACsinθ
ここで、0<θ<πだから、sinθ>0 sinθ= 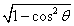
内積の定義から、  ・ ・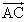 =| =| || ||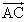 |cosθ |cosθ
したがって、 S= 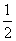 | | || ||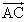 |sinθ= |sinθ=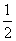 | | || ||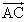 | |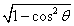
= 
|
 =(x1,y1,0)
=(x1,y1,0)
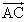 =(x2,y2,0)
=(x2,y2,0)
 |2|
|2|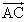 |2-(
|2-( ・
・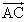 )2
=(x12+y12)(x22+y22)
-(x1x2+y1y2)2
)2
=(x12+y12)(x22+y22)
-(x1x2+y1y2)2
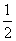 |x12y2-x22y1|
|x12y2-x22y1|
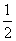 |
| ×
×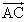 |
|
 ×
×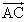 =(y1・0-0・y2 , ・0x2-x1・0 , x1y2-y1x2)
=(0 , 0 , x1y2-y1x2)
=(y1・0-0・y2 , ・0x2-x1・0 , x1y2-y1x2)
=(0 , 0 , x1y2-y1x2)
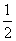 |x12y2-x22y1|
|x12y2-x22y1|