• xのn次多項式f(x)を考える。これを順次、n回微分することで、各項の係数a_nを決定することが出来る。
  
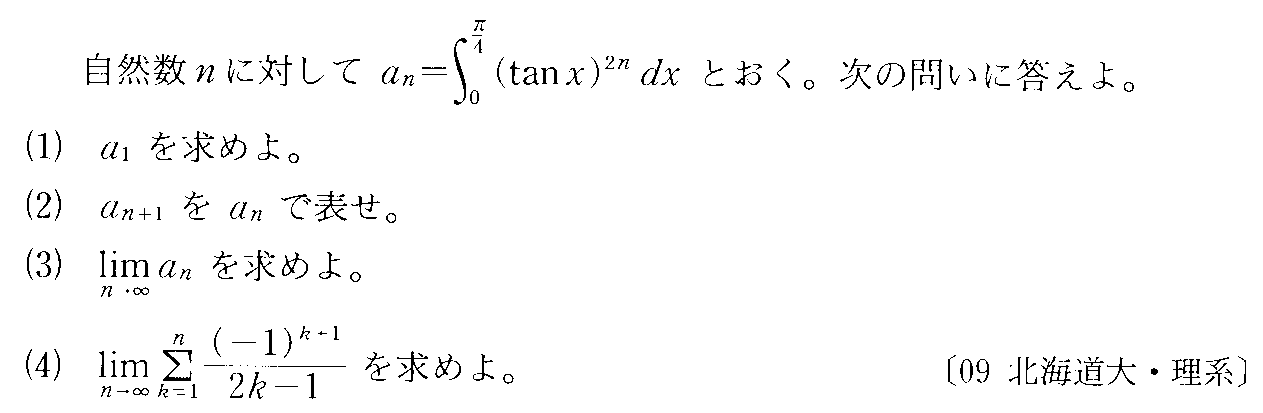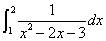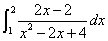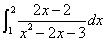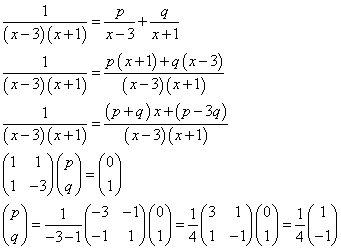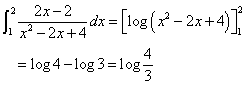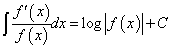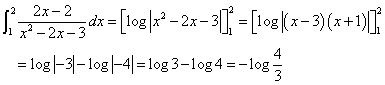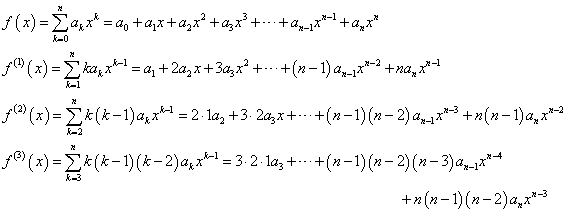
  すなわち、
  
  
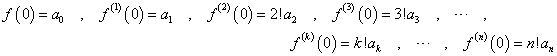
  であるから、
  
  
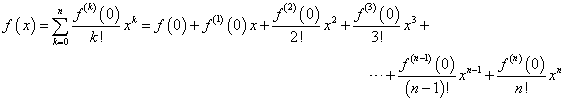
  ということは、ある関数が、無限回微分可能であるとき、これを、n次多項式で「近似」出来ることがわかる。上のnはどこまでも引き延ばすことが出来るから、どこか「途中でやめた」とすれば、それは、「本当の値」とは、少しだけずれてしまうことになるからだ。こういうのを「テーラー級数展開」、または「マクローリン級数展開」による近似と呼ぶ。
  
  
• 逆正接関数y=Atanxについて、マクローリン級数展開をほどこしたいと思う。なぜなら、
  tan(π/4)=1、すなわち、Atan(1)=π/4、4Atan(1)=π
  であるから、これを用いて、πの近似値を得ることが出来るからである。
  
  逆関数とは、xとyを入れ代えた関数のことである。
  関数は、「一つのxに対して一つのyが定まる」ことがその定義であるから、周期関数では、値域すなわちyの範囲に制限を設けないとこの定義を逸脱してしまう。
  
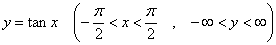
  に対して、
  
  ここから、
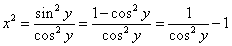  ・・・(1)
  一方、y=tanxの微分は、
  
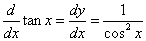
  であるから、xとyを入れ代えて、
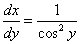  ・・・(2)
  (1)(2)より、
  
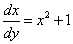
  すなわち、
  
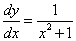
  が得られた。
  
  
• では、順次微分を行っていく。
  
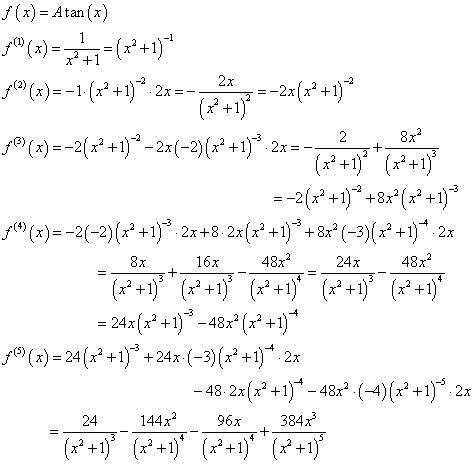
  すなわち、
  
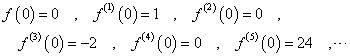
  こうして、
  
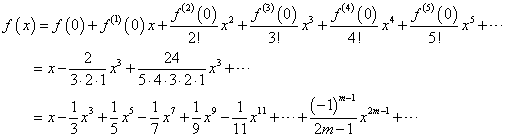
  と、推測される級数展開が得られた。
  しかし、これはいかにも迂遠な方法なのではないだろうか？
  
  
• そこで、次のような関数を考える。マクローリン級数展開の式は、無限項までを考えるかぎり、xについての「恒等式」なのであるから、より単純な関数についての級数展開を得た後、そのx部分に、より複雑な式を「代入」することが、可能なのである！
  
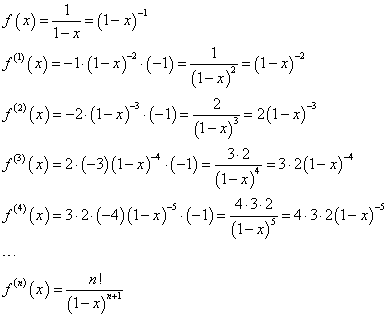
  と、これはいかにも規則性が高い関数なのであった！
  
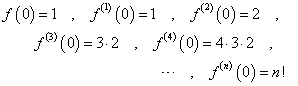
  であるから、第n項までの和で近似すると、
  
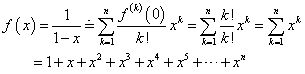
  そこで、上式のxに代えて、-x²を「代入」することによって、逆正接関数y=Atanxの級数展開が得られるではないか？
  すなわち、
  
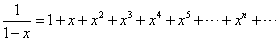
  であるから、
  
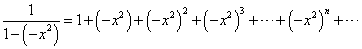
  つまり、
  
  
  
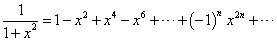
  ところで、
  
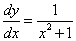
  であったから、項別積分して、
  
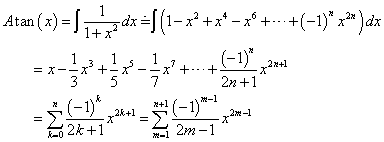
  と、上と同じ結果となった。
  
  
• いよいよ、πの近似式をつくる。
  
  
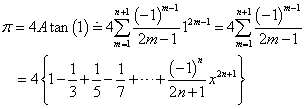
  この級数は、とても収束が遅い。
  100 input n
  110 k=0
  112 a=0
  114 s=0
  120 k=k+1
  122 if k>n then goto 500
  130 a=(-1)^(k+1)/(2*k-1)
  140 s=s+4*a
  142 ss=int(s*1000000)/1000000
  144 d=int((Pi-s)*1000000)/1000000
  150 if int(k/100)*100=k then print k;ss;d
  160 goto 120
  500 end
  
  2000項まで、100項ごとの計算結果と、真の値との差を表示してみた。2000項まで足しても、まだ、小数点以下3桁しか合ってない！
  
  Input ? 2000
  100 3.131592 0.009999
  200 3.136592 0.004999
  300 3.138259 0.003333
  400 3.139092 0.002499
  500 3.139592 0.001999
  600 3.139925 0.001666
  700 3.140164 0.001428
  800 3.140342 0.001249
  900 3.140481 0.001111
  1000 3.140592 0.000999
  1100 3.140683 0.000909
  1200 3.140759 0.000833
  1300 3.140823 0.000769
  1400 3.140878 0.000714
  1500 3.140925 0.000666
  1600 3.140967 0.000624
  1700 3.141004 0.000588
  1800 3.141037 0.000555
  1900 3.141066 0.000526
  2000 3.141092 0.000499
  OK
  
  

  ---

• ところで、この計算をしているときに気づいたのだが、高校の数学で、
  
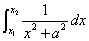
  という積分がx=atantという置換積分で、「うまくいく」ということは、「覚えておかなければならない」事項となっているのだが、「どうしてうまくいくのか？」はちっとも教えてくれない理由が（笑）、わかった。それを説明するには、逆三角関数という、高校数学の範囲を超える、ことになっている内容に触れざるを得ないからなんだね？
  「説明」を、試みよう！
  
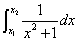• まず、高校数学風に、を解く。
  
  
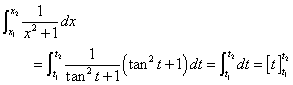
  ここでは、次のような置換積分を用いる。
  
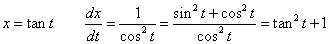
  ただし、

  x	|	x1	→	x2
  ---------------------
  t	|	t1	→	t2

  
  
  
• ところが、上で見たように、
  
  
  
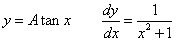
  なのであるから、これはもっと直截に、
  
  
  
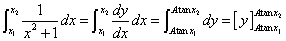
  と見ることができるだろう。
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
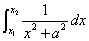• 一般化して、についても、
  
  
  
  
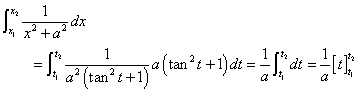
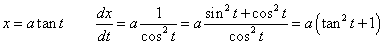
  ただし、

  x	|	x1	→	x2
  ---------------------
  t	|	t1	→	t2

  
  
  これも、
  
  
  
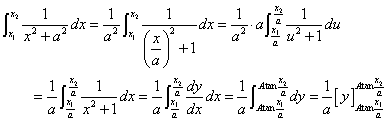
  ここでは、次のような置換積分、
  
  
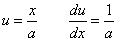
  ただし、

  x	|	x1	→	x2
  ---------------------
  u	|	x1/a	→	x2/a

  
  を用いている。
  
  あるいは、こう考えてもよいだろう？
  
  
  
  
  
  
  
  
• 【例題1】
  
  

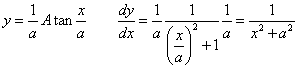
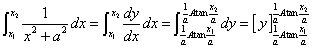
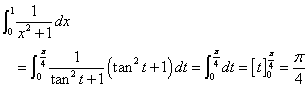
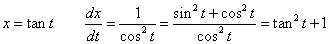
  x	|	0	→	1
  ---------------------
  t	|	0	→	π/4

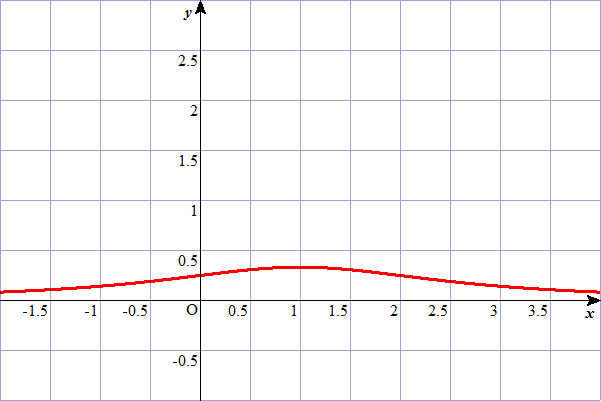
  y=1/(x2+1)の曲線下の面積をx=0から1まで求めると、なるほど、π/4になりそうだ。

  
  
• 【例題2】
  

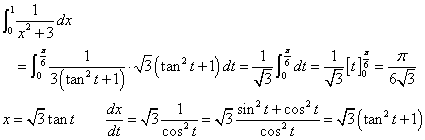
  x	|	0	→	1
  ---------------------
  t	|	0	→	π/6

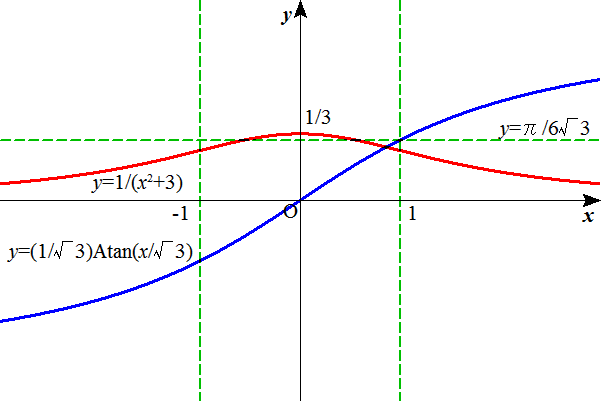  同様にy=1/(x2+3)の曲線下の面積をx=0から1まで求めると、π/6√3。 下に掲げたように、 y=(1/√3)Atan(x/√3) を微分すると y=1/(x2+3) になる。

  
  
  
  
• 【例題3】この方法は、分子が定数、分母がxの2次式で、有理数の範囲では因数分解できないものであるとき、さらに置換を組み合わせることで、適用できる。（分母の2次式が有理数の範囲で因数分解できるときは、部分分数展開による。）
  
  

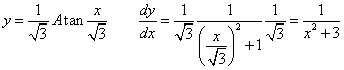
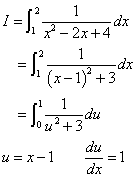
  x	|	1	→	2
  ---------------------
  u	|	0	→	1

  
  

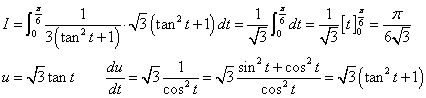
  u	|	0	→	1
  ---------------------
  t	|	0	→	π/6

  この被積分関数は上の【例題2】のy=1/(x²+3)をx軸方向に1、平行移動しただけのものだから、面積が同じなのは当然！
  
  
  
  
• 【例題4】πの近似式を素材にした問題。
  
  
  
  
  
  
  
  
  
  
  
  

【例題4】	【例題4】
【例題4】	【例題4】

【例題4】

• 【例題5】参考までに、分母が2次式であるような定積分のいくつかの形。
  
  
  1. 
  2. 
  3. 
  4. 
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  2. 
     
     部分分数展開
     
     
     
  3. 
     
     これは、
     
     を用いている。
     
     
  4. 
     
     これも、
     
     を用いているのは同じだが、この積分区間では、f(x)が負であることが特徴。