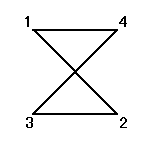
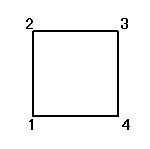
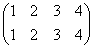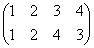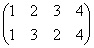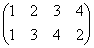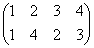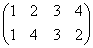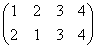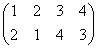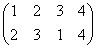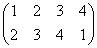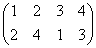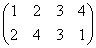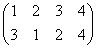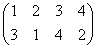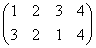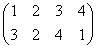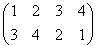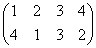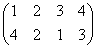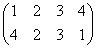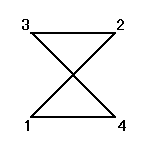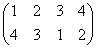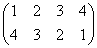下図の一番左上の正三角形、右下の頂点から順に、「反時計回り」に「1,2,3」と番号をつけたものを出発点としよう。
- 正三角形の重心に関して、「反時計回り」に120度回転する「操作」をaと呼び、
- 底辺の垂直二等分線に関して、「裏返す」「操作」をbと呼ぶ
3つの数字「1,2,3」を並べ替える方法の数は、3P3=3!=6通りしかなく、
したがって、得られる正三角形も、下図の6通り以外にはありえない。
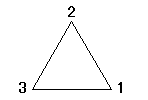 | → b | 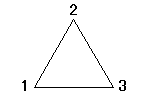 |
| ↓a | ↓ba=a2b | |
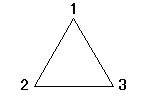 | 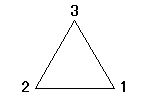 | |
| ↓a2 | ↓ba2=ab | |
 |  |
これを上の「操作」a,bの組み合わせで表示すると、・・・、「操作」の順に左から並べ、続けて行う「操作」を「積」のように、同じ操作の繰り返しは「累乗」のように表記すると、・・・、
下の表の如くになる。
e=a0=b0=a3=b2
|
ba=a2b
| ||||||||||||
ba2=ab
|
a2
| ||||||||||||
a
|
b
|
- これら6個の「操作」の集合をGと呼べば、いかなる「操作」の組み合わせの結果も、Gに含まれるから、「1」の要件は満たす。
- 「操作」については、結合法則が成り立つことが知られている(笑)。
例えば、
(ab)a 1 2 3 3 1 2 2 1 3 1 3 2 a(ba) 1 2 3 3 1 2 2 1 3 1 3 2 - e=a0=b0=a3=b2 は単位元である。
- 逆元について、
- e-1=e
- a-1=a2
- b-1=b
- (ba)-1=a-1b-1=a2b=ba
- (ab)-1=b-1a-1=ba2=ab
- (a2)-1=a
これらの置換に「名前」を付けてみる。
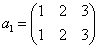  | →→ -π/3回転 | 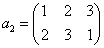 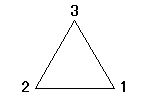 | →→ -π/3回転 | 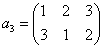 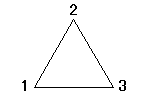 |
| ↓↑左右反転 | ||||
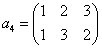 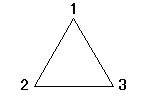 | →→ -π/3回転 | 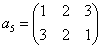 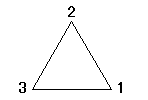 | →→ -π/3回転 | 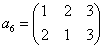  |
- a1:恒等置換
- a2:時計回り、
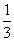 π回転
π回転
- a3:反時計回り、
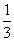 π回転
π回転
- a4:左右反転
- a5:左右反転後、時計回り、
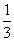 π回転
π回転
- a6:左右反転後、反時計回り、
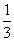 π回転
π回転
- a1=e=a0=b0=a3=b2
- a2=a2
- a3=a
- a4=b
- a5=ba2=ab
- a6=ba=a2b
- a1-1=e-1=e=a1
- a2-1=(a2)-1=a=a3
- a3-1=a-1=a2=a2
- a4-1=b-1=b=a4
- a5-1=(ba2)-1=(a2)-1b-1=ab=a5
- a6-1=(ba)-1=a-1b-1=a2b=a6
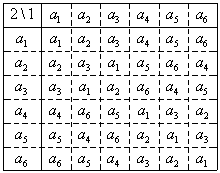
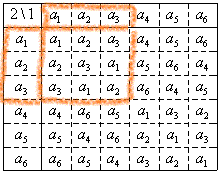
1行目、横に並んでいるa1,a2,・・・が「第1」の操作、
1列目、縦に並んでいるa1,a2,・・・が「第2」の操作、をあらわす。
「交換法則」が成り立たないペアが何組もできていることを、右の表で確認してみた。
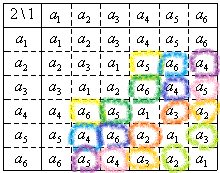
「部分群」というのがあって、
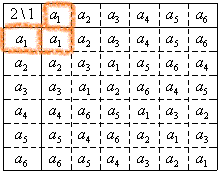
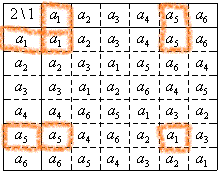
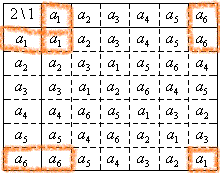
以下の、Gの部分集合、{a1},{a1,a4},{a1,a5},{a1,a6},{a1,a2,a3},
・・・そして、G={a1,a2,a3,a4,a5,a6}は、それぞれが、ちゃんと、「群」の要件を満たしている。


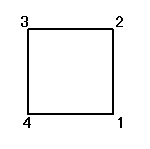
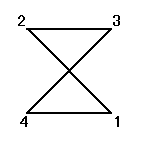
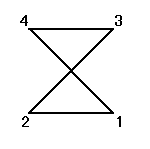
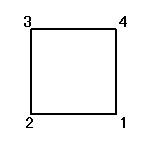
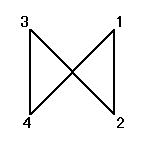
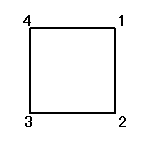
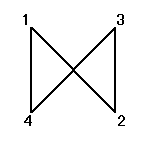
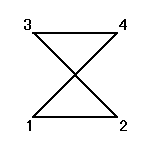
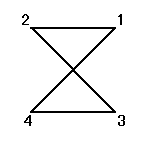
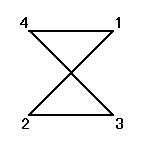
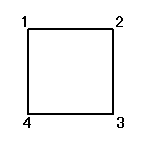
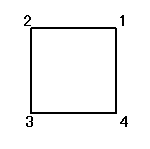
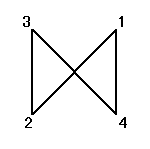
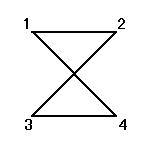
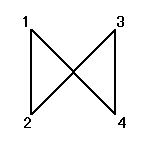
正方形の4頂点に、1,2,3,4と名前をつけ、その順番を並べ替えることを考える。
その並べ替え方の総数は、4P4=4!=24
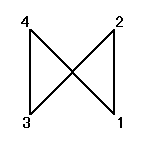
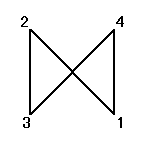
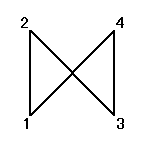
ところが、正三角形の場合と大いに異なるのは、そのほとんどの排列が、正方形になってくれないのであった。
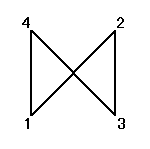
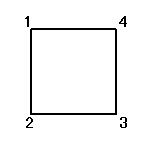
同一直線上にない3点を選べば、かならず三角形が描ける、のに対して、
そのうちのどの3点も同一直線上にないような4点を選んだとしても、その4点のつなぎ方の「順序」によって、4角形になることもあれば、ならないこともあるのだ。
これは、
- 3つの領域はかならず隣接させることができるのに、4つになるとどうしてもできない、
- この世でただ一つ「対角線」を持たない平面図形は、三角形であり、この世でただ一つ「対角線」を持たない立体図形は、四面体である、