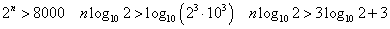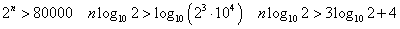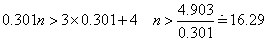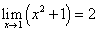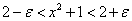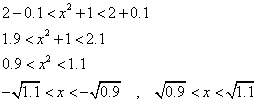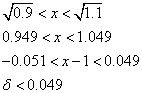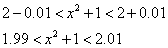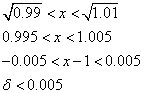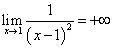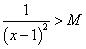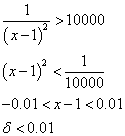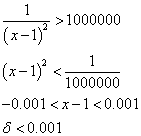定義:「数列に関するコーシーの収束性の定義」:nが限りなく大きくなるとき、数列
a1,a2,・・・,an,・・・
が数aに限りなく近づく、またはaに収束するとは、任意の正数εに対して自然数Nが存在して、不等式
|an-a|<ε
がn≧Nとなるすべてのnについて成り立つことである。
そんな大したことは言ってませんよ(笑)。「限りなく近づく」などという、直感的には誰にでもわかる「日常用語」に、「有無を言わさないような」(笑)数学的な精緻さを与える必要があるのです。
|an-a|<ε
で、εが正の数ですから、
a-ε<an<a+ε
これは、数直線上、「数aのまわりの、わ・り・と・(笑)近く」にanが、いる、と言うことをいっているだけだ。「ど・の・く・ら・い・近くか?」については、まだ、触れていない。
これを、偉そうに言うと(笑)「aのε近傍」となる。「近く」と言ってよかった筈だが、「近傍」、この国の知的伝統では「漢語」で表すほうが、重みがあって、「偉かった」のだな。
ここで、εに「任意性」を与える。正であることは決まっているから、いくらでも大きくすることも出来るし、いくらでもゼロに近づけることが出来る。ほら、ここで「いくらでも近づく」って言葉、使っちゃってるでしょ?、だから、説明は「循環」するの。
それはさておき、εが小さくなれば、aのまわりの「近傍」の幅は、どんどん小さくなっていく。どんどん小さくなった、どこかの時点で、anが「近傍」のエリアから外に出てしまったとしたら、もはや「限りなく近づく」とは言えんだろう?
だから、今度はnの方も、任意でなければならなくなる。ただし、「ある程度大きい」nであってよい。「段々」近づけばよいのだから。その「ある程度」の大きさが、Nで表されている。
平たく言うと、
nをどんどんでかくしていくと、どっか「ある程度でかい」Nを超えたところで、そっからあとはずっとanは、aのまわりの「めちゃめちゃ狭い範囲」にいる、
どんな「めちゃめちゃ狭い範囲」にしても、「めちゃめちゃでかい」nを探し出してきたら、ぜったいその範囲にanをはめこむことができる!
例を挙げてみよう。ということは、
 という数列を考える。当然、
という数列を考える。当然、
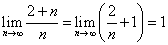 である。ということは、上の定義によれば、
である。ということは、上の定義によれば、
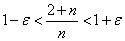 が、εをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成立させることが出来る、そんなNを見つけることが出来る、と言っている。
が、εをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成立させることが出来る、そんなNを見つけることが出来る、と言っている。
εが0.5なら?
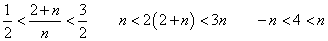
nは自然数だから4より大、つまり5以上。だから、N=5である。
εが0.1なら?
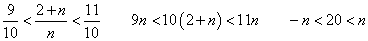
nは自然数だから20より大、つまり21以上。だから、N=21である。
εが0.01なら?
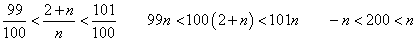
nは自然数だから200より大、つまり201以上。だから、N=201である。
こんなことを繰り返していけば、εがどんなに小さくなっても、Nを大きくとれば、かならず、anを「1のε近傍」に閉・じ・込・め・る・ことが出来るでしょ?
これが、anが1に収束する、ということの、「数学的な」表現、と言うわけだ。
わかっていただけたかしら?、ここでは「数列に関する」となっているが、後に、「関数」の収束性についても同じ議論が行われる。それが「ε-δ論法」だ。数列は、「添え字」になっている独立変数が「自然数」と言う「離散変数」だが、関数は括弧の中に書かれる独立変数が、「実数」と言う「連続変数」だから、少し表現が異なってくるが、言っていることは、ほとんど、同じ。
xが数aに限りなく近づくとき、関数f(x)が数Aに限りなく近づく、またはAに収束するとは、任意の正数εに対して正数δが存在して、
|x-a|<δのとき、つねに、
|f(x)-A|<ε
が成り立つことである。
これも「平たく言って」みよう!
xは、「aのδ近傍」、「数aのまわりの、わりと近く」にいるのだが、δをどんどん小さくしていって「近傍」を狭くしていくと、どっか「ある程度小さい」δより小さくなったところで、そっからあとはずっとf(x)は、Aのまわりの「めちゃめちゃ狭い範囲」にいる、
どんな「めちゃめちゃ狭い範囲」にしても、「めちゃめちゃ小さい」δを探し出してきたら、ぜったいその範囲にf(x)をはめこむことができる!
次は、「発散」。収束しない数列を発散するという。
nが限りなく大きくなるとき、数列
a1,a2,・・・,an,・・・
が限りなく大きくなる、または+∞に発散するとは、どんな正数Mに対しても自然数Nが存在して、
an>M
がn≧Nとなるすべてのnについて成り立つことである。
平たく言うと、
nをどんどんでかくしていくと、どっか「ある程度でかい」Nを超えたところで、そっからあとはずっとanは、Mより「ある程度でかい」ところにいる、
Mを「どんなにでかい」数にしても、「めちゃめちゃでかい」nを探し出してきたら、ぜったいその「とてもでかい」Mよりもさらに「でかい」範囲にanを押し出すことができる!
例を挙げてみよう。ということは、
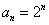 という数列を考える。当然、
という数列を考える。当然、
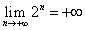 である。ということは、上の定義によれば、
である。ということは、上の定義によれば、
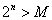 が、Mをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成させることが出来る、そんなNを見つけることが出来る、と言っている。
が、Mをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成させることが出来る、そんなNを見つけることが出来る、と言っている。
Mが8000なら?
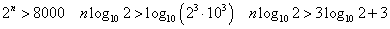
log102=0.301とすると、

nは自然数だから13以上。だから、N=13である。
Mが80000なら?
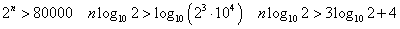
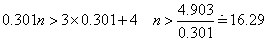
nは自然数だから17以上。だから、N=17である。
こんなことを繰り返していけば、Mがどんなに大きくなっても、Nを大きくとれば、かならず、anを「Mの右側」に押・し・出・す・ことが出来る。
これの「関数」版。
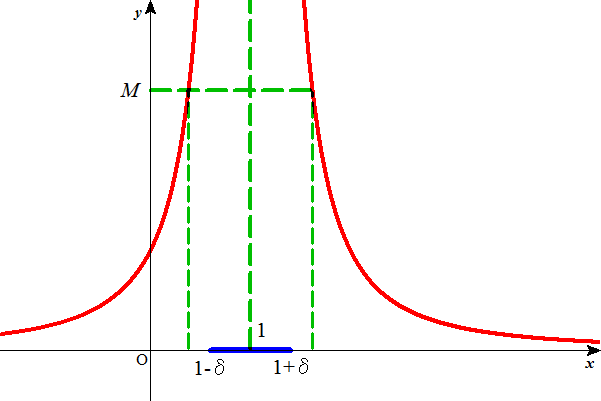
xが数aに限りなく近づくとき、関数f(x)が正の無限大になるとは、任意の正数Mに対して正数δが存在して、
|x-a|<δのとき、つねに、
f(x)>M
が成り立つことである。
「関数」版、収束の場合と、発散の場合、それぞれ例を作ってみた。
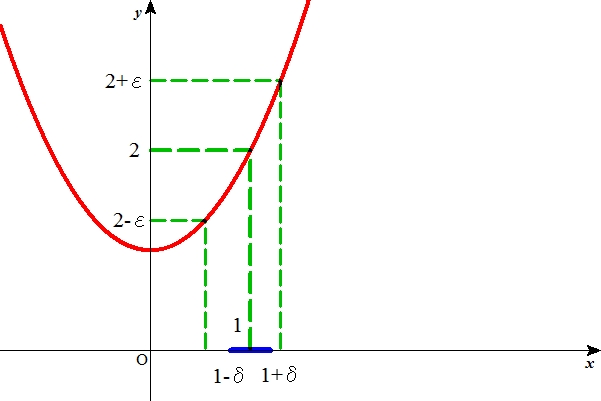
収束の場合。
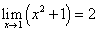
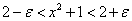
ε=0.1とすると、
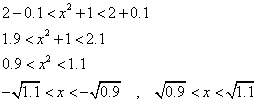
xは1の「近傍」で考えるから、
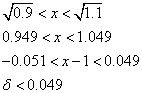
ε=0.1に対しては、0.049より小さな数をδとして選べばよい。すなわち、このεに対しては、ちゃんとδが「存在」している。
ε=0.01とすると、
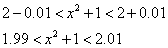
同様に、xは1の「近傍」で考えるから、
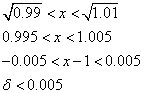
ε=0.01に対しては、0.005より小さな数をδとして選べばよい。すなわち、このεに対しても、ちゃんとδが「存在」している。
・・・
以下同様、εをどんなに小さくしても、それに対応するδが、ちゃんと「存在」している。
発散の場合。
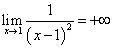
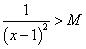
M=1000とすると、
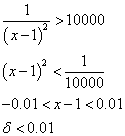
M=1000に対しては、0.01より小さな数をδとして選べばよい。すなわち、このMに対しては、ちゃんとδが「存在」している。
M=100000とすると、
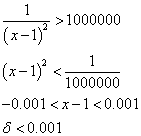
M=100000に対しては、0.001より小さな数をδとして選べばよい。すなわち、このMに対しても、ちゃんとδが「存在」している。
・・・
以下同様、Mをどんなに大きくしても、それに対応するδが、ちゃんと「存在」している。
 という数列を考える。当然、
という数列を考える。当然、
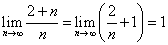 である。ということは、上の定義によれば、
である。ということは、上の定義によれば、
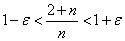 が、εをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成立させることが出来る、そんなNを見つけることが出来る、と言っている。
が、εをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成立させることが出来る、そんなNを見つけることが出来る、と言っている。
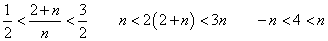
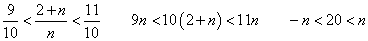
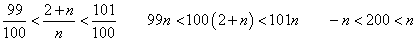
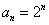 という数列を考える。当然、
という数列を考える。当然、
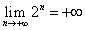 である。ということは、上の定義によれば、
である。ということは、上の定義によれば、
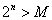 が、Mをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成させることが出来る、そんなNを見つけることが出来る、と言っている。
が、Mをどうとっても、nをある程度大きく、Nより大きくとったら、かならず成させることが出来る、そんなNを見つけることが出来る、と言っている。