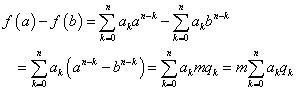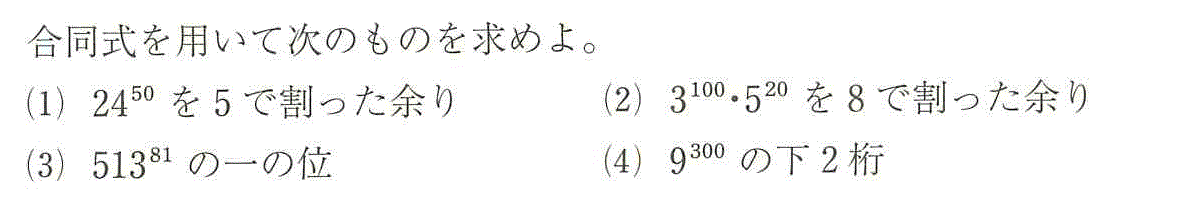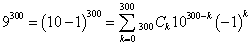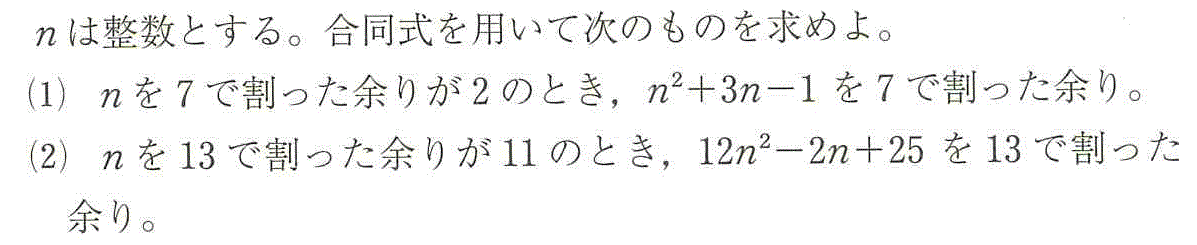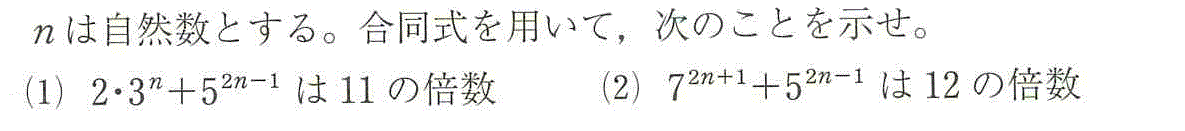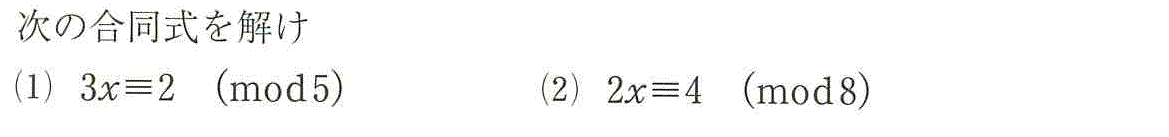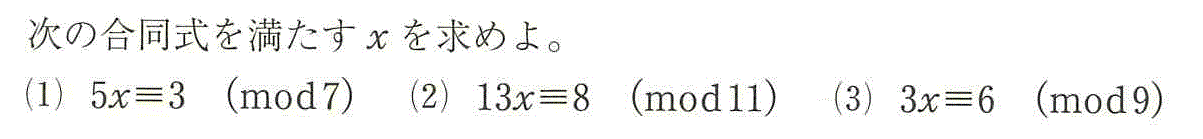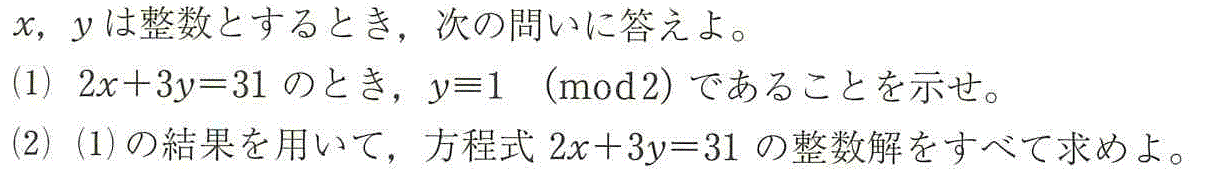「合同式congruence_equation」の研究
- [定義]
整数a,b,mに対して、
a-bがmの整数倍のとき、
aはmを法modulusとしてbと合同である、といい、
a≡b (mod m)と書く。
- [定理1]a≡b (mod m)となるための必要十分条件は、a,bをmで割った余りが等しいことである。
[証明]
- a≡b (mod m)→a,bをmで割った余りが等しいを示す。
a,bをmで割った余りをそれぞれr1,r2とおくと、
a=ma'+r1ただし、0≦r1<m
xb=mb'+r2ただし、0≦r2<m
a-b=m(a'-b')+(r1-r2)・・・(1)
ここで、
0≦r1<m
-m<-r2≦0
であるから、
-m<r1-r2<m・・・(2)
一方、a≡bであるから、a-bは、mの整数倍であり、
(1)式より、r1-r2もmの整数倍でなければならない。
(2)の範囲の中でこれを満たすのは、r1-r2=0のみである。
よって、r1=r2
- a,bをmで割った余りが等しい→a≡b (mod m)を示す。
a,bをmで割った余りがいずれもrとすると、
a=ma'+r
b=mb'+r
ただし、0≦r<m
a-b=m(a'-b')
a-bはmの整数倍である。
- [定理2]mを法とするとき、次の3式(同値律)がなりたつ。
- 反射律 a≡a (mod m)
- 対称律 a≡b (mod m)ならばb≡a (mod m)
- 推移律 a≡b (mod m),b≡c (mod m)ならばa≡c (mod m)
[証明]
- a=ma'+rただし、0≦r<m、とすると、
a-a=0すなわち、a≡a
- a≡b (mod m)から、
a=ma'+r,b=mb'+rただし、0≦r<m
b-a=m(b'-a')よって、b≡a
- a≡b (mod m)から、
a=ma'+r,b=mb'+rただし、0≦r<m
b≡c (mod m)から、
b=mb'+r,c=mc'+rただし、0≦r<m
a-c=m(a'-c')よって、a≡c
- [定理3]a≡b (mod m),c≡d (mod m)のとき、次の各式が成立する。
- a+c≡b+d (mod m)
- a-c≡b-d (mod m)
- ac≡bd (mod m)
- an≡bn (mod m)ただしnは自然数
[証明]
a≡b (mod m)より、a-b=mq1
c≡d (mod m)より、c-d=mq2
- (a+c)-(b+d)=(a-b)+(c-d)=m(q1+q2)
- (a-c)-(b-d)=(a-b)-(c-d)=m(q1-q2)
- ac-bd=(b+mq1)(d+mq2)-bd
=bmq2+dmq1+m2q1q2
=m(bq2+dq1+mq1q2)
- 数学的帰納法による。
- n=1のときa≡b (mod m)・・・(ア)
- n=kに対して、an≡bk (mod m)と仮定。
iiiより、aak≡bbk (mod m)
すなわち、ak+1≡bk+1 (mod m)・・・(イ)
(ア)(イ)より、任意の自然数nに対して、an≡bn (mod m)
- [定理3・系1]
a≡b (mod m)のとき、任意の整数nに対して、
a≡b+mn (mod m)
[証明]
a≡b (mod m)より、a-b=mq
a-(b+mn)=mq-mn=m(q-n)
- [定理3・系2]
整数係数の整式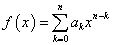 に対して、
に対して、
a≡b (mod m)のとき、f(a)≡f(b) (mod m)
[証明]
a≡b (mod m)だから、k=0,1,2,・・・,n-1に対して、[定理3iv]より、
an-k≡bn-k (mod m)
また、a0≡b0 (mod m)
よって、k=0,1,2,・・・,nに対して、an-k≡bn-k (mod m)
an-k≡bn-k=mqkと書くことができる。
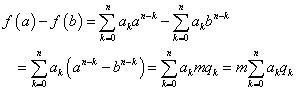
- [定理4]ac≡bc (mod m)のとき、(c,m)=gならば、
a≡b (mod m/g)
ここに、(c,m)=gとは、c,mの最大公約数がgであることをあらわす。
[証明](c,m)=gより、c=gc',m=gm'とおくことができる。
ここに、(c',m')=1すなわち、c',m'は互いに素である。
ac≡bc (mod m)より、ac-bc=mq=gm'q
一方、ac-bc=c(a-b)=gc'(a-b)
すなわち、gm'q=gc'(a-b)
すなわち、m'q=c'(a-b)
(c',m')=1だから、a-bはm'で割り切れる。すなわち、a-bはm/gで割り切れる。
- [定理4・系]ac≡bc (mod m)のとき、(c,m)=1ならば、
a≡b (mod m)
- [定理3i〜iii]では、「加・減・乗」の3つの演算に関しては、「合同式」が通常の数式の等式と同様に扱えることが明らかになった。
しかし、「除」に関しては、[定理4・系]が示すように、序数と法が互いに素であるときに限り、行うことができる。
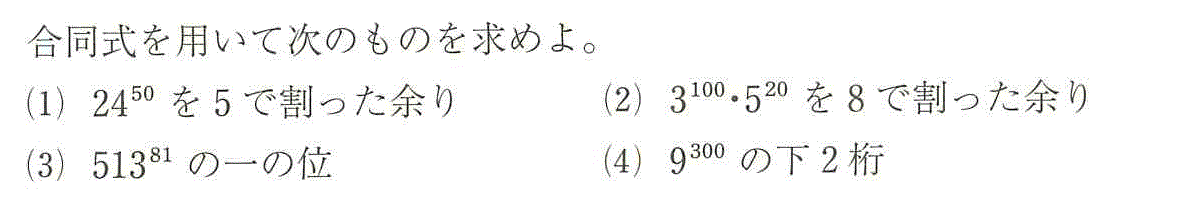
- (1)24≡4 (mod 5)、[定理3iv]より、2450≡450 (mod 5)
450=1625、16≡1 (mod 5)、同様に、1625≡125 (mod 5)
よって、2450≡1 (mod 5)
- (2)3100520=9502510
9≡1 (mod 8)、25≡1 (mod 8)だから、
[定理3iv]より、950≡1 (mod 8)、2510≡1 (mod 8)
[定理3iii]より、9502510≡1 (mod 8)
すなわち、3100520≡1 (mod 8)
- (3)51381を10で割った余りを求めればよい。
513≡3 (mod 10)、[定理3iv]より、51381≡381 (mod 10)
381=34×20+1=8120×3
81≡1 (mod 10)、[定理3iv]より、8120≡1 (mod 10)
[定理3iii]より、8120×3≡1×3 (mod 10)
よって、51381≡3 (mod 10)
- (4)9300を100で割った余りを求めればよい。
二項定理より、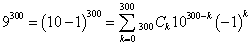
右辺のk=0からk=298に対応する項はすべて100で割り切れるから、
9300≡300C299101(-1)299+300C300100(-1)300≡300・10・(-1)+1≡1 (mod 100)
よって、9300≡1 (mod 100)
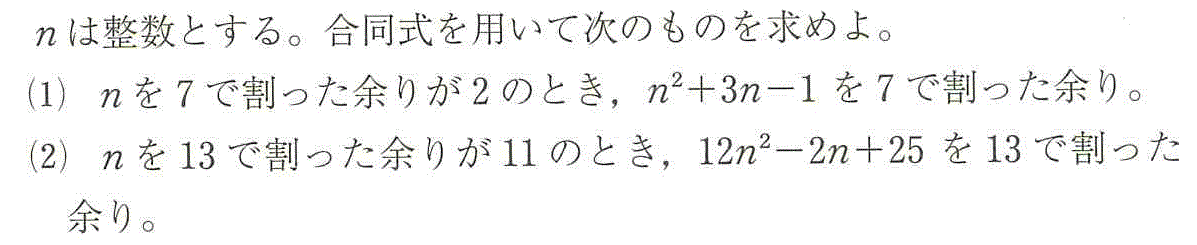
- (1)n≡2 (mod 7)だから、
[定理3iv]より、n2≡22≡4 (mod 7)
[定理3iii]より、3n≡3・2≡6 (mod 7)
[定理3i,ii]より、n2+3n-1≡4+6-1≡9≡2 (mod 7)
- (2)n≡11 (mod 13)だから、
[定理3iv、系1]より、n2≡112≡121≡13×9+4≡4 (mod 13)
[定理3iii、系1]より、12n2≡12×4≡48≡13×3+9≡9 (mod 13)
[定理3iii、系1]より、2n≡2×11≡22≡13×1+9≡9 (mod 13)
[定理3i,ii、系1]より、12n2-2n+25≡9-9+25≡25≡13×1+12≡12 (mod 13)
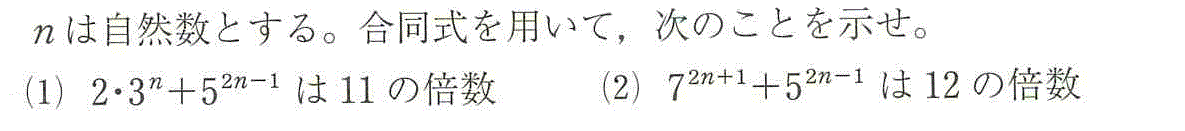
- (1)2・3n+52n-1≡0 (mod 11)を示したい。
52n-1=52(n-1)+1=5・25n-1
25≡3 (mod 11)、[定理3iii,iv]より、5・25n-1≡5・3n-1 (mod 11)
[定理3i]より、
2・3n+5・25n-1≡2・3n+5・3n-1≡6・3n-1+5・3n-1≡11・3n-1≡0 (mod 11)
よって、2・3n+52n-1≡0 (mod 11)
- (2)72n+1+52n-1≡0 (mod 12)を示したい。
72n+1+52n-1=72n+1+52(n-1)+1=7・(72)n+5・(52)n-1=7・49n+5・25n-1
[定理3・系1]より、49≡12×4+1≡1 (mod 12)、25≡12×2+1≡1 (mod 12)
[定理3iv,iii,i]より、7・49n+5・25n-1≡7・1n+5・1n-1≡7+5≡12≡0 (mod 12)
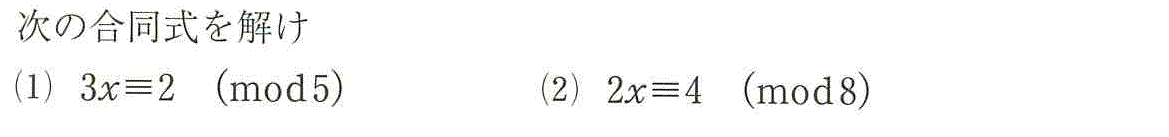
- (1)3を何倍かして、5で割ると1余る数にしたい。
3x≡2 (mod 5)
[定理3iii]より、6x≡4 (mod 5)
[定理3・系1]より、5x+x≡x≡4 (mod 5)
- (2)3を何倍しても、8で割ると1余る数にはできない。
これは、[定理4]の適用場面で、
2x≡4 (mod 8)
(2,8)=2だから、つまり、2と8の最大公約数は2だから、
x≡2 (mod 4)
「合同式を解く」とは、未知数xの与えられた法に対する剰余を求めることだから、
x≡□ (mod 8)でなければならない。
x≡2 (mod 4)から、x-2=4qすなわち、x=4q+2
4で割ると2余る数を、8で割った余りは?、これは、qが2の倍数であるか否かで異なる。
- q=2q'のとき・・・x=8q'+2すなわち、x≡2 (mod 8)
- q=2q'+1のとき・・・x=8q'+6すなわち、x≡6 (mod 8)
よって、x≡2,6 (mod 8)
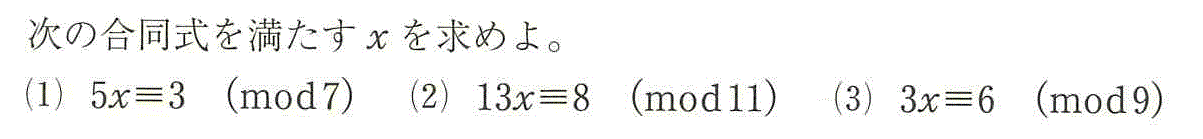
- (1)5を何倍かして、7で割ると1余る数にしたい。
5x≡3 (mod 7)
[定理3iii]より、15x≡9≡2 (mod 7)
[定理3・系1]より、2×7x+x≡x≡2 (mod 7)
- (2)13を何倍かして、11で割ると1余る数にしたい。78=13×6=11×7+1
13x≡8 (mod 11)
[定理3iii]より、78x≡48≡4 (mod 11)
[定理3・系1]より、7×11x+x≡x≡4 (mod 11)
- (3)3x≡6 (mod 9)
(3,9)=3であるから、[定理4]より、x≡2 (mod 3)
すなわち、x=3q+2
qを3の剰余類に分類する。
- q=3q'のとき、・・・x=9q'+2
- q=3q'+1のとき、・・・x=9q'+5
- q=3q'+2のとき、・・・x=9q'+8
よって、x≡2,5,8 (mod 9)
ところで、「解のない」合同式(合同方程式)が存在する。
[定理5]合同式ax≡b (mod m)は、(a,m)がbを割り切るとき、そのときだけ解をもつ。
[例]2x≡5 (mod 4)は、解をもたない。
2x-5=4q
左辺は奇数であり、右辺は偶数であるから、このような整数x,qは存在しない。
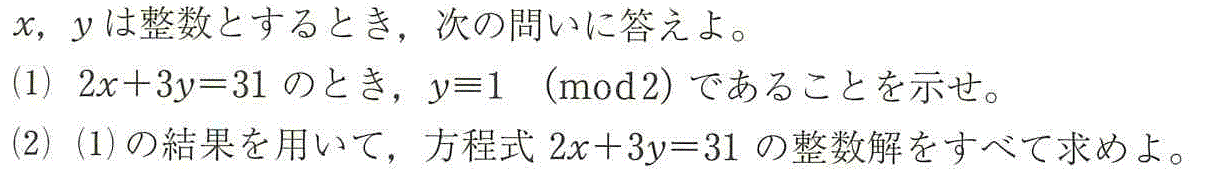
- (1)x,yの係数を比較すると、2より3の方が大きいから、3=2×1+1として、
2x+3y≡2x+(2×1+1)y≡y (mod 2)
一方、31≡1 (mod 2)
よって、y≡1 (mod 2)
- (2)y=2k+1 (kは整数)とすると、
2x+3y=31
2x+3(2k+1)=31
2x+6k=28
x+3k=14
x=-3k+14
よって、整数kに対して、(x,y)=(-3k+14,2k+1)

- (1)11x+13y=23
11x+13y≡11x+(11+2)y≡2y (mod 11)
23≡2×11+1≡1 (mod 11)
よって、2y≡1 (mod 11)
12y≡11y+y≡y≡6 (mod 11)
y=11k+6 (kは整数)とすると、
11x+13(11k+6)=23
11x+13×11k=23-78=-55
x+13k=-5
よって、整数kに対して、(x,y)=(-13k-5,11k+6)
- (2)39x-29y=326
39x-29y≡(29+10)x-29y≡10x (mod 29)
326≡29×11+7≡7 (mod 29)
よって、10x≡7 (mod 29)
30x≡29x+x≡x≡21 (mod 29)
x=29k+21 (kは整数)とすると、
39(29k+21)-29y=326
39×29k-29y=326-39×21=326-819=493=-29×17
39k-y=-17
よって、整数kに対して、(x,y)=(29k+21,39k+17)
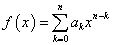 に対して、
に対して、