(2,3)=1であるから、2x'+3y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(31x',31y')である。
2x'+3y'=1を解く。・・・(イ)
x',y'の係数2,3を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(2,3)=1、すなわち、2と3は互いに素であるから、かならずこれは可能である。
2x'+(2×1+1)y'=1
2(x'+y')+y'=1
こうして、第2項の係数が1となった。
明らかに、x'+y'=0,y=1は、解である。
この連立方程式を解くと、
(x',y')=(-1,1)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が絶対値において3より小さい正数であり、かつ、y'が2より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
2x'+3y'=1・・・(イ)
2(-1)+3・1=1・・・(ウ)
2(x'+1)+3(y'-1)=0・・・(イ)-(ウ)
すなわち、
2(x'+1)=-3(y'-1)
ここに、(2,3)=1であるから、
x'+1=-3k
y'-1=2k
すなわち、
(x',y')=(-3k-1,2k+1)
無論、k=0のときが、上の、
x'が絶対値において3より小さい正数であり、かつ、y'が2より小さい正数である特殊解、
(x',y')=(-1,1)
である。
では、
x'が3より小さい正数であり、かつ、y'が絶対値において2より小さい正数である特殊解、
の方はどうか?
k=-1とすればよい。すなわち、
(x',y')=(2,-1)
(ア)に戻ると、解は次のように書ける。
(x,y)=(31(-3k-1),31(2k+1))
もう少しシンプルな表現にしたい。k'=31kとおくと、
(x,y)=(-3k'-31,2k'+31)
さらに、たとえば、k''=k'+15とおくと、
(x,y)=(-3(k''-15)-31,2(k''-15)+31)=(-3k''+14,2k''+1)
または、たとえば、k'''=k'+10とおくと、
(x,y)=(-3(k'''-10)-31,2(k'''-10)+31)=(-3k'''-1,2k'''+11)
ここでも、端数の絶対値を31より小さくする方法が、ただ2通り、存在するのである。
- (1)11x+13y=23・・・(ア)
(11,13)=1であるから、11x'+13y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(23x',23y')である。
11x'+13y'=1を解く。・・・(イ)
x',y'の係数11,13を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(11,13)=1、すなわち、11と13は互いに素であるから、かならずこれは可能である。
11x'+(11×1+2)y'=1
11(x'+y')+2y'=1
(2×5+1)(x'+y')+2y'=1
2{5(x'+y')+y'}+(x'+y')=1
2(5x'+6y')+(x'+y')=1
こうして、第2項の係数が1となった。
明らかに、5x'+6y'=0,x'+y=1は、解である。
この連立方程式を解くと、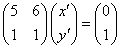
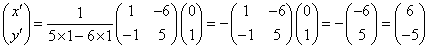
(x',y')=(6,-5)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が13より小さい正数であり、かつ、y'が絶対値において11より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
11x'+13y'=1・・・(イ)
11・6+13(-5)=1・・・(ウ)
11(x'-6)+13(y'+5)=0・・・(イ)-(ウ)
すなわち、
11(x'-6)=-13(y'+5)
ここに、(11,13)=1であるから、
x'-6=-13k
y'+5=11k
すなわち、
(x',y')=(-13k+6,11k-5)
無論、k=0のときが、上の、
x'が13より小さい正数であり、かつ、y'が絶対値において11より小さい正数である特殊解、
(x',y')=(6,-5)
である。
では、
x'が絶対値において13より小さい正数であり、かつ、y'が11より小さい正数である特殊解、
の方はどうか?
k=1とすればよい。すなわち、
(x',y')=(-7,6)
(ア)に戻ると、解は次のように書ける。
(x,y)=(23(-13k+6),23(11k-5))
もう少しシンプルな表現にしたい。k'=23kとおくと、
(x,y)=(-13k'+23×6,11k'-23×5)
23×6=13×10+8,23×5=11×10+5であるから、
さらに、たとえば、k''=k'-10とおくと、
(x,y)=(-13(k''+10)+13×10+8,11(k''+10)-11×10-5)=(-13k''+8,11k''-5)
23×6=13×11-5,23×5=11×11-6であるから、
または、たとえば、k'''=k'-11とおくと、
(x,y)=(-3(k'''+11)+13×11-5,11(k'''+11)-11×11+6)=(-13k'''-5,11k'''+6)
ここでも、端数の絶対値を23より小さくする方法が、ただ2通り、存在するのである。 - (2)39x-29y=326・・・(ア)
(39,29)=1であるから、39x'-29y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(326x',326y')である。
39x'-29y'=1を解く。・・・(イ)
x',y'の係数の絶対値39,29を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(39,29)=1、すなわち、39と29は互いに素であるから、かならずこれは可能である。
(29×1+10)x'-29y'=1
29(x'-y')+10x'=1
(10×2+9)(x'-y')+10x'=1
10{2(x'-y')+x'}+9(x'-y')=1
10(3x'-2y')+9(x'-y')=1
(9×1+1)(3x'-2y')+9(x'-y')=1
9{(3x'-2y')+(x'-y')}+(3x'-2y')=1
9(4x'-3y')+(3x'-2y')=1
こうして、第2項の係数が1となった。
明らかに、4x'-3y'=0,3x'-2y=1は、解である。
この連立方程式を解くと、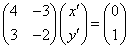
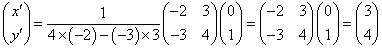
(x',y')=(3,4)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が29より小さい正数であり、かつ、-y'が絶対値において39より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
39x'-29y'=1・・・(イ)
39・3-29・4=1・・・(ウ)
39(x'-3)-29(y'-4)=0・・・(イ)-(ウ)
すなわち、
39(x'-3)=29(y'-4)
ここに、(39,29)=1であるから、
x'-3=29k
y'-4=39k
すなわち、
(x',y')=(29k+3,39k+4)
無論、k=0のときが、上の、
x'が29より小さい正数であり、かつ、-y'が絶対値において39より小さい正数である特殊解、
(x',y')=(3,4)
である。
では、
x'が絶対値において29より小さい正数であり、かつ、-y'が39より小さい正数である特殊解、
の方はどうか?
k=-1とすればよい。すなわち、
(x',y')=(-26,-35)
(ア)に戻ると、解は次のように書ける。
(x,y)=(326(29k+3),326(39k+4))
もう少しシンプルな表現にしたい。k'=326kとおくと、
(x,y)=(29k'+326×3,39k'+326×4)
326×3=29×33+21,326×4=39×33+17であるから、
さらに、たとえば、k''=k'+33とおくと、
(x,y)=(29(k''-33)+29×33+21,39(k''-33)+39×33+17)=(29k''+21,39k''+17)
326×3=29×34-8,326×4=39×34-22であるから、
または、たとえば、k'''=k'+34とおくと、
(x,y)=(29(k''-34)+29×34-8,39(k''-34)+39×34-22)=(29k''-8,39k''-22)
ここでも、端数の絶対値を326より小さくする方法が、ただ2通り、存在するのである。