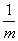 +
+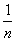 は集積点にあらざることを証せよ。
は集積点にあらざることを証せよ。
結論が「否定文」となっているから、証明は「背理法」または「対偶」によるのが都合がよい、と想像される。
A→Bが「真」であるのは、集合で表せば、
∀x∈Aに対して、x∈B、・・・、Aの任意の元xがBの元であること、に等しいから、これは、
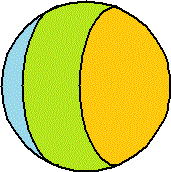
A⊂B、つまり、AがBに包含されていること、になる。ベン図で表せば、下図のようになる。

ところで、図からわかるように、
A⊂Bであることは、A∩BC=φ、Aと「Bの補集合」が共通部分を持たない、ことと同じい。
ということは、「AならばBである」を示すには、
「Aであり」、かつ、「Bでない」ことが決して起り得ないことを示せばよいことになる。
まさにそのような「起こり得ないこと」を仮定してみて、それが矛盾をきたすことを導けば、矛盾が導けた瞬間に、証明ができたことになるのである。これが「背理法」のロジックである。中身をよりよく表す言葉としては、「帰謬法」、誤謬に帰する、の方がふさわしいが、「謬」が当用漢字でない、などの理由で、高校教科書などでは「背理法」と呼ぶようになったと思われる。
同様に、図からわかるのは、ベン図は、全体集合が平面上の長方形で表されているから、その四囲に「無限」が隠されてしまっているが、これを「位相幾何学的同型性」を保ちながら、つまり、ぐにゃぐにゃと、4辺を紙面の「向こう側」で接続してしまえば、たちまち、「無限」を含んだ「リーマン球」が立ち現れる。
長方形の4辺が結び合わさった「へそ」が、このボールの左端、青色の部分の真中あたりにあると思いねぇ。
そうすると、オレンジ色の部分が集合A、
緑色の部分は、Aの外側で、Bの内側、つまりAC∩B
ならば、オレンジと緑を合わせれば、A∪(AC∩B)=(A∪AC)∩(A∪B)=U∩(A∪B)=A∪Bで、
ここではA⊂Bだから、A∪B=B、なぜなら、
∀x∈Aに対して、A⊂Bだから、x∈B、
∀x∈Bに対して、もちろん、x∈B、
したがって、∀x∈A∪Bに対して、x∈B、よって、(A∪B)⊂B、次に、
∀x∈Bに対して、x∈A∪B、よって、B⊂(A∪B)、以上、(A∪B)=B
とすると、残る青色部分は、Bの補集合、BCである。こうして、
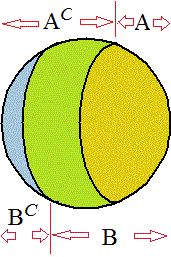
こうして、わかったことは、上図の如く、Bの補集合は、Aの補集合に、包含されている、すなわち、BC⊂AC、
これは、¬B→¬Aが真であることに対応している。これが「ある命題が真であれば、その『対偶』はかならず真である」の、意味である。
こうして、ともに「AならばB」を示すにあたって、
「背理法」は、「Aであり、かつ、『Bでない』と仮定して矛盾を導く」技術、
「対偶」は、「『Bでない』ならば、『Aでない』」を示す技術、
であることがわかった。何のた・め・に・、そのような技術が必要であるかを考えるに、二つに共通するのは、いずれも「Bでない」から出発する点である、つまり、元の命題の結論部分B、が、も・と・も・と・、「否定文」で書かれていた場合、「存在しない」ことを証明するのは通常困難であるから、これを、「Bでない」という「肯定文」に転換することができるメリットがあるのだ。
では、証明に入ろう。
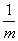 +
+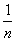 は集積点ではない、が示すべきことがらである。これは一見「A→B」という命題らしい形をとっていない。Bという結論しかなくて、Aという条件がないのである。つまり、無条件、したがって、Aにあたる部分を「全体集合U」に擬してよいことになる。したがって、命題、
は集積点ではない、が示すべきことがらである。これは一見「A→B」という命題らしい形をとっていない。Bという結論しかなくて、Aという条件がないのである。つまり、無条件、したがって、Aにあたる部分を「全体集合U」に擬してよいことになる。したがって、命題、
「・・・ならば、
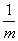 +
+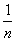 は集積点ではない」を、「U→B」とみて、
は集積点ではない」を、「U→B」とみて、
「背理法」によるならば、U∩BC=φを、
「対偶」によるならば、BC⊂UCを、それぞれ示すことになる。
ところで、U∩BC=BC、UC=φであるから、
結局どちらも、BC=φを示すことになる。つまり、
「
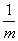 +
+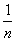 が集積点であると仮定したら、矛盾を導く」、ことを言えばよい。
が集積点であると仮定したら、矛盾を導く」、ことを言えばよい。
[証明]
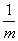 +
+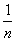 が集積点であるとする。
が集積点であるとする。
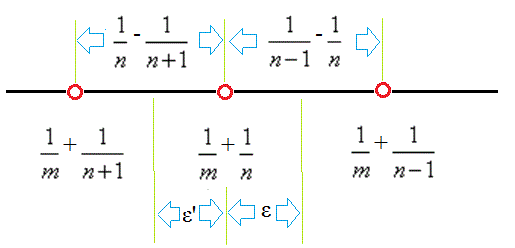
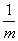 +
+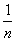 に隣接するSの要素は、
に隣接するSの要素は、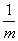 +
+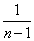 (n=m+2,m+3,・・・)、または、
(n=m+2,m+3,・・・)、または、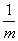 +
+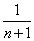 (n=m+1,m+2,・・・)であるが、
(n=m+1,m+2,・・・)であるが、
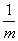 +
+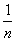 と
と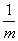 +
+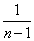 の間には、Sの要素はただ一つも含まれていないから、
の間には、Sの要素はただ一つも含まれていないから、
両者の間隔
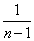 -
-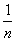 よりも小さい値としてεを選ぶと、区間(
よりも小さい値としてεを選ぶと、区間(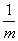 +
+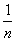 ,
,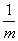 +
+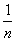 +ε)には、Sの要素が含まれず、
+ε)には、Sの要素が含まれず、
同様に、
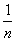 -
-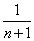 よりも小さい値としてε'を選ぶと、区間(
よりも小さい値としてε'を選ぶと、区間(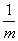 +
+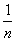 -ε,
-ε,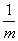 +
+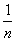 )には、Sの要素が含まれないことになり、これでは、
)には、Sの要素が含まれないことになり、これでは、
任意の正数εに対して、区間(
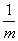 +
+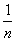 -ε,
-ε,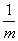 +
+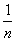 +ε)に無数のSの要素が含まれる、とはいえない。
+ε)に無数のSの要素が含まれる、とはいえない。
したがって、
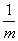 +
+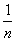 が集積点ではなく、これを集積点であるとする仮定が誤っていたことがわかった。証明終わり。
が集積点ではなく、これを集積点であるとする仮定が誤っていたことがわかった。証明終わり。
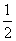 ,
,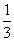 ,・・・,
,・・・,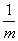 ,・・・の外に集積点なきを証せよ。
,・・・の外に集積点なきを証せよ。
[証明]m=2,3,・・・、n=m+1,m+2,・・・に対して、
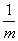 +
+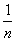 はいずれも集積点ではない。
はいずれも集積点ではない。
よって、0及
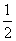 ,
,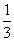 ,・・・,
,・・・,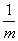 ,・・・以外に集積点は存在しない。
,・・・以外に集積点は存在しない。
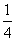 等、一般に、
等、一般に、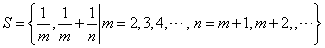

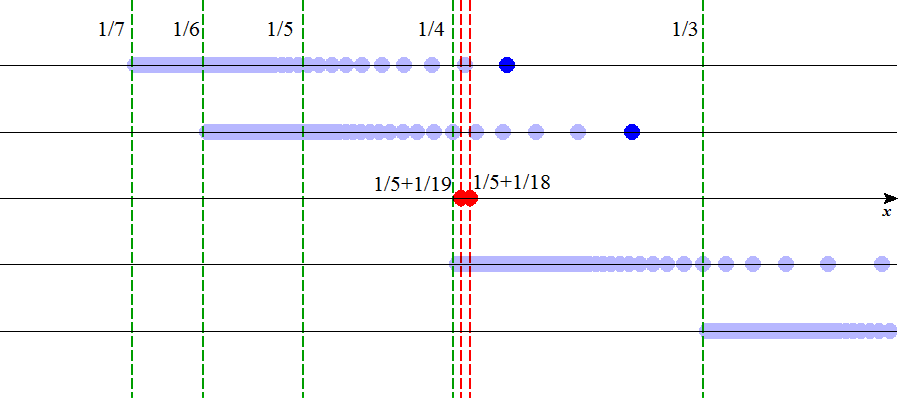
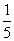 +
+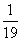 と
と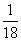 の間には、決して「無数」ではなく、有限個のSの要素しか含まれていないことを確かめたい。
の間には、決して「無数」ではなく、有限個のSの要素しか含まれていないことを確かめたい。
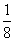 +
+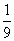 ≒0.236 ,
≒0.236 , 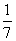 +
+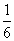 +
+

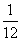 =0.25 ,
=0.25 , 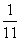 ≒0.258なのである。
≒0.258なのである。
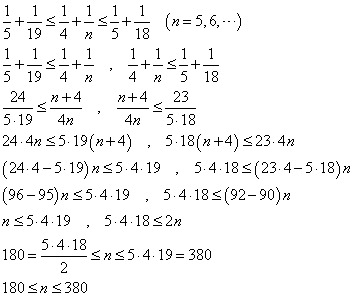
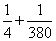 から、
から、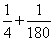 まで、両端を含めると201個、含めないと199個の要素が、この区間に存在している。
まで、両端を含めると201個、含めないと199個の要素が、この区間に存在している。