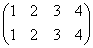
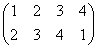


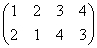
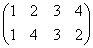
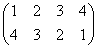
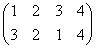
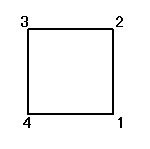
a1=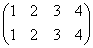 | a1=e | 恒等置換 |
a2=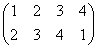 | a2=a3 | 時計回りπ/4回転 |
a3= | a3=a2 | 反時計回りπ/2回転 |
a4= | a4=a | 反時計回りπ/4回転 |
a5=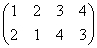 | a5=b | 左右反転 |
a6=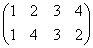 | a6=ba3=ab | 左右反転後、時計回りπ/4回転 |
a7=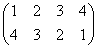 | a7=ba2=a2b | 左右反転後、反時計回りπ/2回転 |
a8=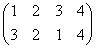 | a8=ba=a3b | 左右反転後、反時計回りπ/4回転 |
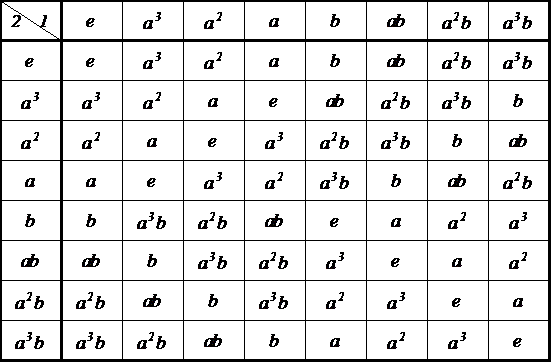
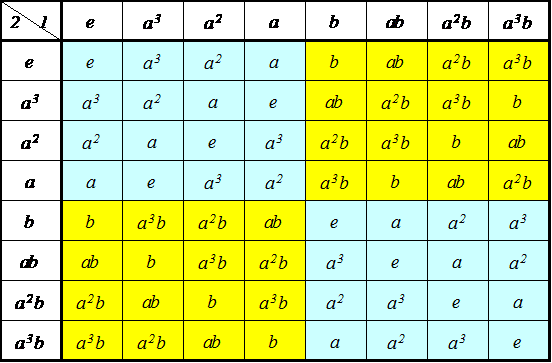
 を全体としてa1'、
を全体としてa1'、 を全体としてa2'、と呼び、集合G'={a1',a2'}とし、
を全体としてa2'、と呼び、集合G'={a1',a2'}とし、

|
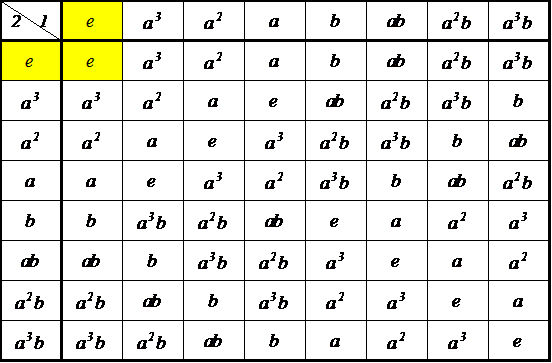
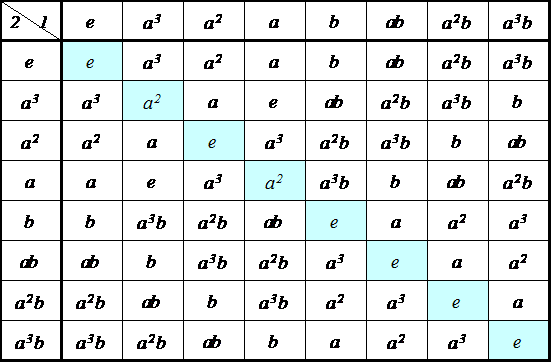
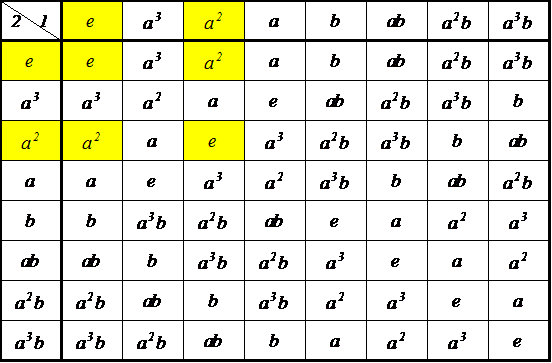
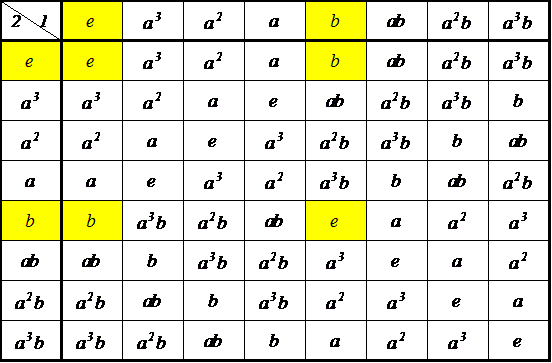
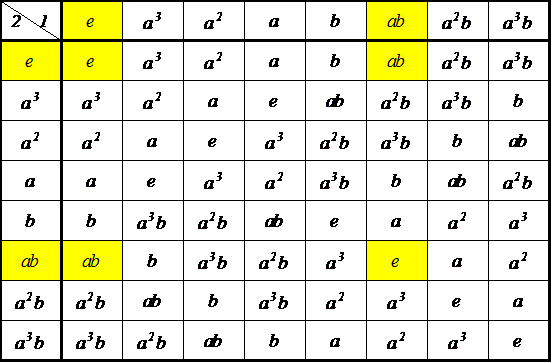

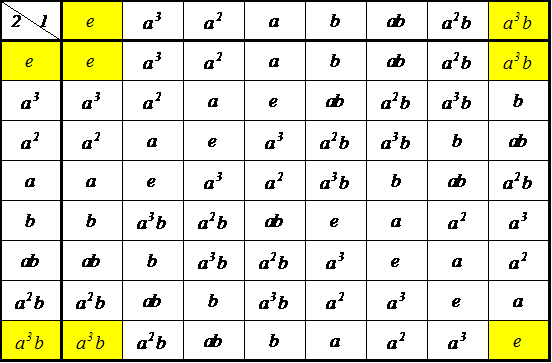
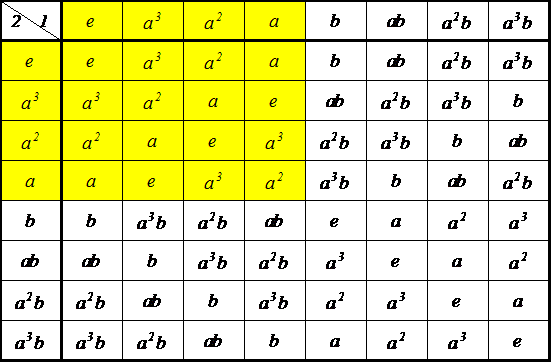
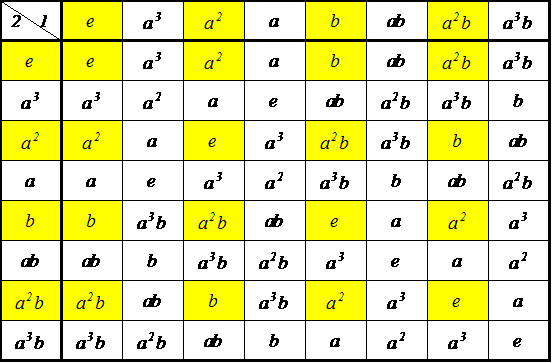
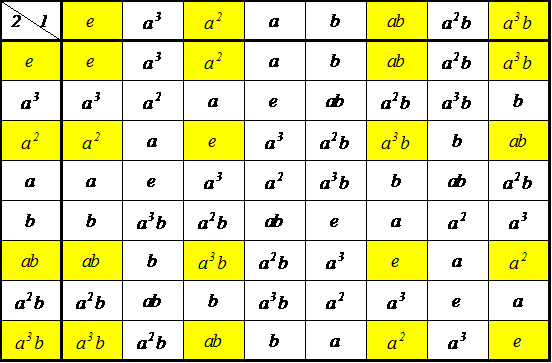
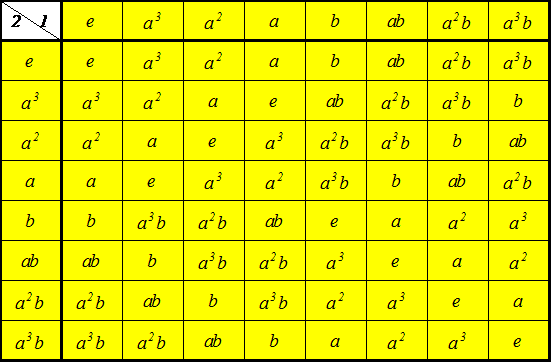
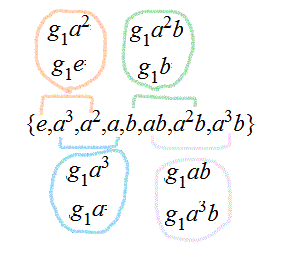
| 左剰余類 | |||
| g3e={e,ab} g3ab={ab,e} | g3a3={a3,a2b} g3a2b={a2b,a3} | g3a2={a2,a3b} g3a3b={a3b,a2} | g3a={a,b} g3b={b,a} |
| 右剰余類 | |||
| eg3={e,ab} abg3={ab,e} | a3g3={a3,b} bg3={b,a3} | a2g3={a2,a3b} a3bg3={a3b,a2} | ag3={a,a2b} a2bg3={a2b,a} |