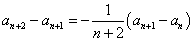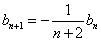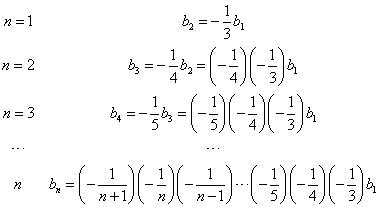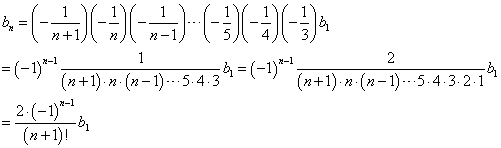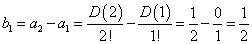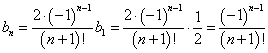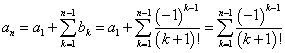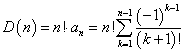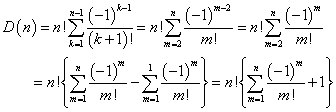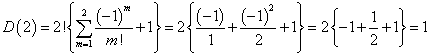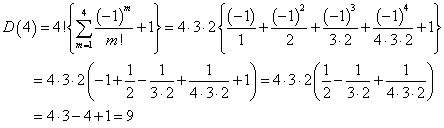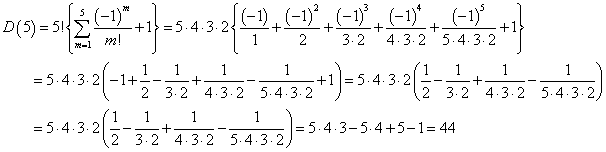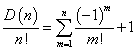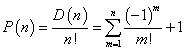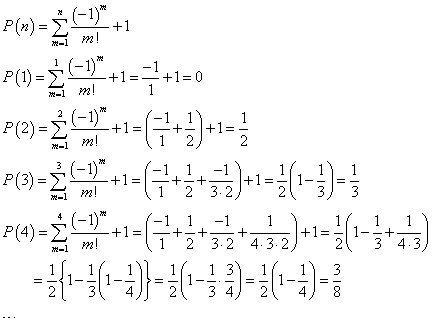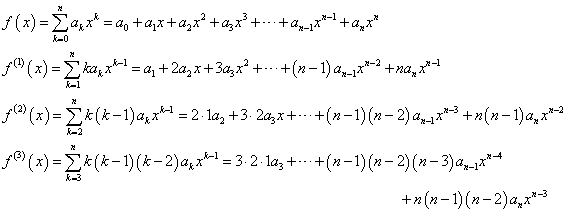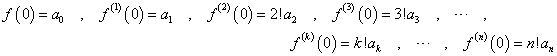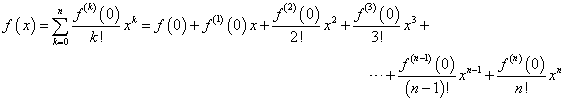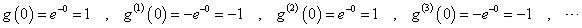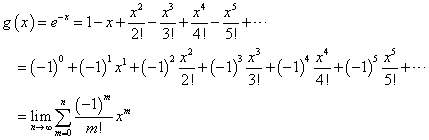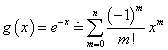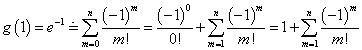1からnまでのn個の自然数を左から右へと適当に並べた配列は、nPn=n!通りあるが、それらのうち、左端から数えた番号と、そこにある自然数とが、ただ一つも一致しないような配列をn次の「完全順列」と呼ぶことにする。
別の言い方をすると、k=1,2,3,・・・,nに対して、数列akを次のように定める。
- 任意のn以下の自然数kに対して、akは、自然数1,2,3,・・・,nのうちのいずれかである。
- 任意のn以下の自然数の組i≠jに対して、ai≠ajである。
- そして、任意のn以下の自然数kに対して、ak≠kである。
こうして得られた数列akは、n次の「完全順列」である。
n次の「完全順列」全体の集合をA(n)、その要素の個数をD(n)と呼ぶことにする。
n=2,3,4,5について、具体例を挙げる。
- n=2のとき、A(2)は、次のただ一つであり、D(2)=1である。
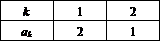
- n=3のとき、A(3)は、次の2つしかなく、D(3)=2である。


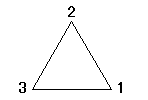 →
→ →
→
これは、上のような正三角形を、順次、1を2に、2を3に、3を1に、すりかえることによって得られる配列である。
ちなみに、数字1,2,3の並べ方は、3!=6通りあるが、他の4通りは、すべて、「完全順列」の要件を満たさない。網掛け部分がak≠kでないからである。




- n=4のとき、A(4)は、次のようになり、D(4)=9である。

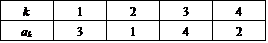
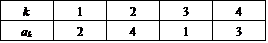
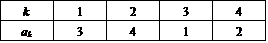




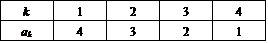
これは、たとえば次のようにして発見できる。

網掛け部分には、2,3,4のいずれかが入るが、2ならば、

ならば、ak=1を入れる場所は、k=2,3,4のどれかであるから、3通りある。
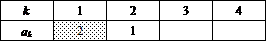 →
→
 →
→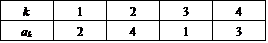
 →
→
網掛け部分が、3ならば、、

やはり、ak=1を入れる場所は、k=2,3,4のどれかであるから、3通りある。
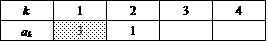 →
→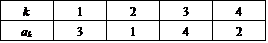
 →
→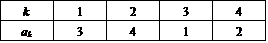
 →
→
網掛け部分が、4ならば、、

やはり、ak=1を入れる場所は、k=2,3,4のどれかであるから、3通りある。
 →
→
 →
→
 →
→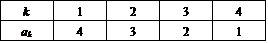
- 同様にして、n=5のとき、A(5)は、次のようになり、D(5)=44である。












































D(n)を求める「漸化式」を得たい。
ものの本には、その解として、D(n+2)=(n+1){D(n+1)+D(n)}
と書かれているから、それを「見てしまった」(笑)ところから始めることにする。
D(n+2)を導くのに、D(n+1)のみならず、D(n)が必要であるらしい。
直接隣接する前項D(n+1)のみでは、D(n+2)が決定できない。
ということは、集合A(n+1)の要素、D(n+1)個の一つ一つから、一定の手続きによってA(n+2)の要素全部を、「生成」することができないことを意味する。

逆に言うと、A(n+2)の要素全部に、この手続きの逆の手続きを施しても、決してA(n+1)の要素にたどり着かないものが存在することになる。
集合A(n+1)の要素から、A(n+2)の要素を生成する手続きとしては、次のようなものが紹介されている。
- A(n+1)の要素の右端に、
 を付け加える。
を付け加える。

- ajとn+2とを、入れ替える。

j=1,2,3,・・・,n+1だから、j≠n+2
aj=1,2,3,・・・,n+1だから、aj≠n+2
したがってこれは、n+2次の完全順列である。
- その個数はいくつあるか?
j=1,2,3,・・・,n+1の中から、どれを選んでもよいから、n+1通り。
D(n+1)個の、A(n+1)の要素に対して、この手続きができるから、それによって得られるn+2次の完全順列は、
(n+1)D(n+1)個である。
例を挙げると、A(4)の一つの要素、
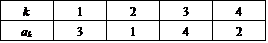
に対して、右端に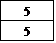 を付け加え
を付け加え

これは完全順列ではないから、「5」を何かと交換しなければならない。その方法は、「3,1,4,2」の4通りあり、次の4つの、5次の完全順列が得られる。




同様にして、
 から、
から、




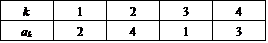 から、
から、




 から、
から、




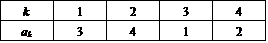 から、
から、




 から、
から、




 から、
から、




 から、
から、




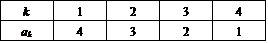 から、
から、




がそれぞれ生成される。
次にすべきことは、この手続きを逆にたどって、A(n+2)の要素から、A(n+1)の要素に復元できないものがあるらしいのだが、その性質を明らかにしたい。
先に具体例から見る。
A(5)の一つの要素、
 で、aj=5であるものを探す。
で、aj=5であるものを探す。
j=3であるから、a3とa5を入れ替える。

これは完全順列ではないから、右端の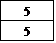 を切り離す。
を切り離す。

これは、4次の完全順列である。ところが、
A(5)の別の一つの要素、
 で、aj=5であるものを探す。
で、aj=5であるものを探す。
j=3であるから、a3とa5を入れ替える。

これは完全順列ではないから、右端の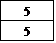 を切り離す。
を切り離す。

これは、4次の完全順列ではない!
違いはどこにあるのか?
はじめの例では、入れ替えは、 と
と で行われた。3,4,5という3個の数字が関与している。
で行われた。3,4,5という3個の数字が関与している。
あとの例では、入れ替えは、 と
と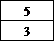 で行われた。3,5という2個の数字だけで入れ替えが可能。
で行われた。3,5という2個の数字だけで入れ替えが可能。
これが原因のようである。
さて、このように、1列のみ、番号と値が一致してしまっている「不完全順列」に対して、次のような操作を行ってみる。
問題の1列を除去する。

1,2,○,4と、飛んでいる番号を前づめにすると、

これは3次の完全順列のうちの一つである。どうやら、A(5)のいくつかのの要素は、この「逆」の手続きによって、2つ次元の低いA(3)の要素と対応しているらしいことがわかる。
ここから、推測して一般化を試みる。
A(n+2)のすべての要素に対して、aj=n+2となるものを探すことができる。

この、j列と、n+2列とを入れ替えて、

n+2列とを切り離したとき、

- n+1次の完全順列である場合と、
- 1列のみ番号と値が一致した不完全順列である場合、
が生ずる。
- 入れ替える2列が、
 と
と が、
が、 と
と のような関係、すなわち、
のような関係、すなわち、
aj=n+2であるが、an+2≠jのときは、n+1次の完全順列になるが、
- 入れ替える2列が、
 と
と が、
が、 と
と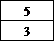 のような関係、すなわち、
のような関係、すなわち、
aj=n+2かつ、an+2=jのときは、1列のみ番号と値の等しいn+1次の「不完全順列」となる。
このときは、等しい1列を除去し、飛んだ番号を前につめれば、n次の完全順列に対応させることができる。
A(5)からA(3)の場合について、iiのパターンの例をすべて挙げておく。
 →
→
 →
→
 →
→
 →
→
 →
→
 →
→
 →
→
 →
→
ここまでの検討で、A(n+2)のすべての要素のうち、
- 一部は、A(n+1)に対応付けられ、
- 残りは、A(n)に対応付けられることがわかった。
この対応は、「多対1」であるから、ふたたび、A(n)または、A(n+1)の各要素から、「1対多」対応によって、A(n+2)を生成する手続きをまとめてみよう。
iに関しては、すでに述べたものを再録する。
-
- A(n+1)の要素の右端に、
 を付け加える。
を付け加える。

- ajとn+2とを、入れ替える。

j=1,2,3,・・・,n+1だから、j≠n+2
aj=1,2,3,・・・,n+1だから、aj≠n+2
したがってこれは、n+2次の完全順列である。
- その個数はいくつあるか?
j=1,2,3,・・・,n+1の中から、どれを選んでもよいから、n+1通り。
D(n+1)個の、A(n+1)の要素に対して、この手続きができるから、それによって得られるn+2次の完全順列は、
(n+1)D(n+1)個である。
-
- A(n)のすべての要素の、両端または間の、n+1か所のうち、左からi番目に、
 を1列挿入する。
を1列挿入する。


番号をずらす。

1列のみ、番号と値の一致する、n+1次の不完全順列が得られる。
- 右端に、
 を付け加える。
を付け加える。

bi=iと、bn+2=n+2を入れ替える。

これはn+2次の完全順列である。
A(n)のすべての要素について、 を挿入する場所がn+1か所あるから、
を挿入する場所がn+1か所あるから、
その個数は、(n+1)D(n)である。
i,iiをまとめて、
D(n+2)=(n+1){D(n+1)+D(n)}
が得られた。
BASICで、完全順列を書き出すプログラムを作ってみた。
100 dim c(10)
1000 input n
1010 amin=1
1020 count=0
1100 for i=1 to n-1
1200 amin=10^i+amin
1300 next i
1310 amax=n*amin
1400 for i=amin to amax
1410 t=i
1500 for j=1 to n
1600 c(j)=t-int(t/10)*10
1610 t=int(t/10)
1700 next j
2100 for j=1 to n
2200 t=c(j)
2300 for k=1 to n
2400 if k=j then goto 2600
2500 if c(k)=t then goto 3000
2505 if c(n-k+1)=k then goto 3000
2510 if c(k)>n then goto 3000
2520 if c(k)=0 then goto 3000
2600 next k
2700 next j
2710 count=count+1
2800 print i;
3000 next i
3100 print "(";n;"-";count;")"
9999 end
演算結果は次の通り。
- n=2のとき、D(2)=1
- n=3のとき、D(3)=2
- n=4のとき、D(4)=9
- n=5のとき、D(5)=44
- n=6のとき、D(6)=265
- n=7のとき、D(7)=1854
- n=8のとき、D(8)=14833
確かに、
- n=2のとき、D(4)=3(D(3)+D(2))=3(2+1)=9
- n=3のとき、D(5)=4(D(4)+D(3))=4(9+2)=44
- n=4のとき、D(6)=5(D(5)+D(4))=5(44+9)=265
- n=5のとき、D(7)=6(D(6)+D(5))=6(265+44)=1854
- n=6のとき、D(8)=7(D(7)+D(6))=7(1854+265)=14833
となっている!
n=2,3,4,5,6,7,8の、完全順列全リスト
次に考えるのは、当然、この、隣接3項間漸化式は「解けるのか?」という問題である。解けない漸化式はざらにある。むしろ「解けない」ことが一般で、例外的に「解」すなわち、第n項をnの関数として表示する方法が存在する。
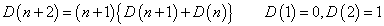
両辺を(n+2)!で割る。

すなわち、
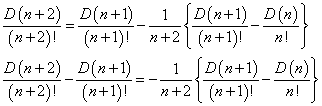
ここで、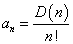 とおくと、
とおくと、
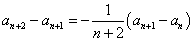
さらに、anの階差数列をbnとおく、すなわち、次のように定めると、
bn=an+1-an
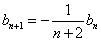
具体的に書き出してみると、
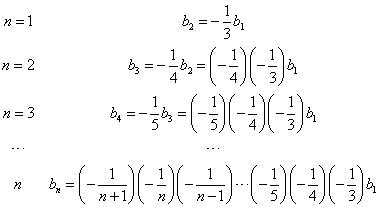
すなわち、
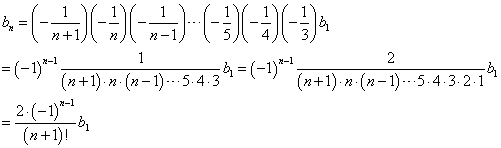
ここで、
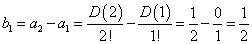
だから、
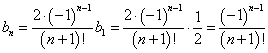
こうして階差数列の一般項が、与えられたのだから、anは、
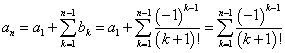
もとのD(n)に戻すと、
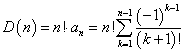
ここで、m=k+1なる、変数変換をほどこすと、k=1→n-1ならば、m=2→nであるから、
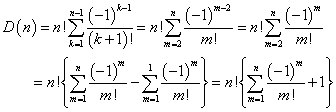
を得た。これは、「解けた」ことにはなっていない。右辺にΣ記号が残っている。これは、連続変数の場合にたとえれば、f(x)を定義する式の右辺にほかならぬf(x)の積分が現れている事態に等しい。しかし、それは両辺を微分すれば、f(x)とその1階微分の関係を表す1次式になっているのだから、線形1階微分方程式であり、ふたたび離散変数の場合の喩えに戻すと、ここでは、「隣接3項間漸化式」、すなわち、2階差分方程式であったものが、1階差分方程式までは、還元された、と考えてよい、と、思う(笑)。
確かめてみよう。
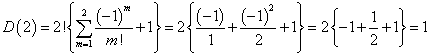

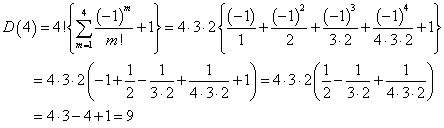
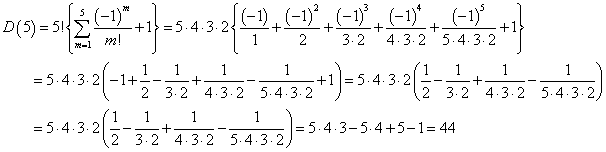
さて、

この式の「意味」について考える。両辺をn!で割って、
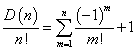
左辺は何を意味しているかを考えるに、nPn=n!であるから、分母は、自然数1,2,3,・・・,nの「順列」である。
全順列に対する、「完全順列」の割合、・・・、1,2,3,・・・,nと書かれたカードを並べたときに、それが、「完全順列」となっている「確率」を表しているようである。
これを、P(n)と書くことにする。すなわち、
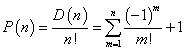
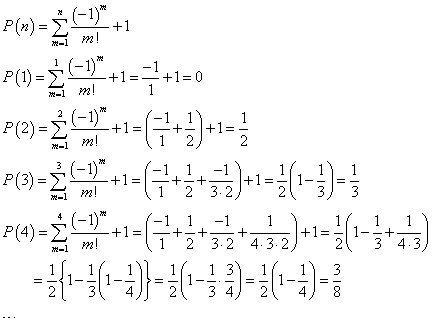
唐突だが、ここで「マクローリン級数展開」による、関数の近似、を思い出す。
xのn次多項式f(x)を考える。これを順次、n回微分することで、各項の係数anを決定することが出来る。
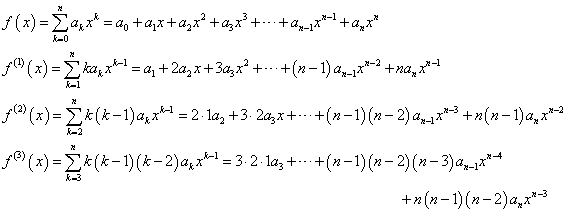
すなわち、
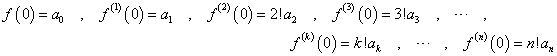
であるから、
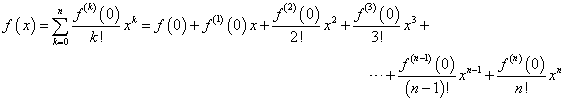
ということは、ある関数が、無限回微分可能であるとき、これを、n次多項式で「近似」出来ることがわかる。上のnはどこまでも引き延ばすことが出来るから、どこか「途中でやめた」とすれば、それは、「本当の値」とは、少しだけずれてしまうことになるからだ。こういうのを「テーラー級数展開」、または「マクローリン級数展開」による近似と呼ぶ。
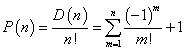
の形に似せようとすれば、項番号の偶奇にともなって正負が入れ替わるのだから、微分を繰り返したとき、そのようなことが生じるのは、g(x)=e-xが思い浮かぶ。

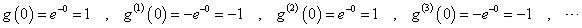
すなわち、
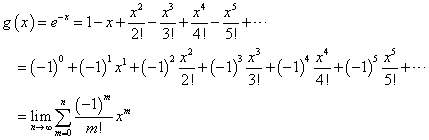
すなわち、関数g(x)=e-xの、マクローリン級数展開による第n項までの近似値が、
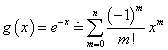
である。これは当然、xに関する恒等式であるから、x=1を代入することも可能である。
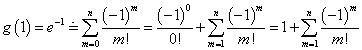
なんと、右辺は、P(n)そのものではないか!
つまり、全順列に対する、完全順列の確率は、e-1に収束することが示されてしまったのである!
では、やってみよう。n=20まで計算してみた。e-1=0.367839441・・・ということだから、すでにn=12あたりでほぼ完全に収束している。
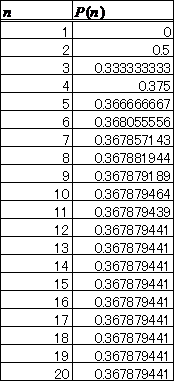
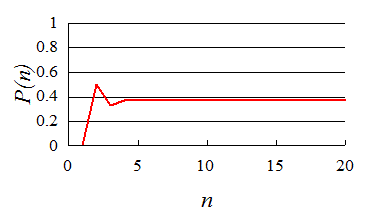
最後に、若干の考察。

この式から感じられるのは、(-1)mが含まれていることから、何か「偶奇性」(parity)が関与しているらしい、こと。振り返ってみよう。
集合A(n+2)には、A(n+1)由来のものとA(n)由来のものとが「排反的」に、「互いに素」に、含まれていて、A(n+1)の像、とA(n)の像との「直和」集合(互いに素な集合の合併集合)として、集合A(n+2)が得られたのであった。
そして、それら二つの排反的な要素の違いを決定付けるのが、一方は、
 →
→ →
→
のように、1を2に、2を3に、3を1に、という三者の関与する(確かこれを「巡回置換」と呼んだと思う)入れ替え、
もう一方は、
 と
と のような、3を5に、5を3に、と、二者のみの関与する置換、という相互に還元することが不可能な二つの方法なのであった。
のような、3を5に、5を3に、と、二者のみの関与する置換、という相互に還元することが不可能な二つの方法なのであった。
言うまでもなく、2は最初の偶数の素数であり、3は最初の奇数の素数である。無論2と3は互いに素であるから、いかなる自然数も、2と3の1次結合、2x+3yによって生成することができる。
つまり、1,2,3,・・・,nと並んだ配列を、順次、変形して完全順列にもっていく方法は、かならず、これら三者間の巡回置換、二者間の相互入れ替え、の組み合わせとして表現できる筈なのである。
nが偶数なら、すべて巡回置換、すべて相互入れ替え、あるいは両者の混合、の方法がありうるが、nが奇数なら、奇数を偶数のみで生成することは不可能だから、巡回置換のみ、または、複数回の相互入れ替えと、かならず、少なくとも一回の巡回置換を要するだろう。こんな風に、「偶奇性」が、はっきりと顔を出す筈なのである。
だとすれば、最初から、ほら、こんな漸化式が成り立つのだ!、証明してみろ!
D(n+2)=(n+1){D(n+1)+D(n)}
みたいなアプローチは、「本末転倒」、とも思えなくもないが(笑)、数学はカントールに倣えば(笑)「自由」なのであり、どこからアプローチしなければならないと言う「王道」はないのであるが、・・・。
 →
→ →
→

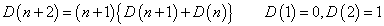

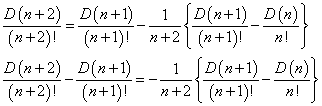
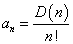 とおくと、
とおくと、