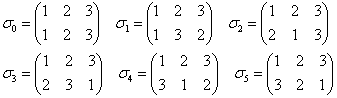「不変量と対称性」今井淳、寺尾宏明、中村博昭（ちくま学芸文庫）

1. 集合G={a₁,a₁,・・・,a_n,・・・}は有限もしくは無限の集合で、
   その上に2変数の関数φ(a,b)=cが定義され、その値は常にGに属する。
   このφ(a,b)=cをab=cで表わす。
2. 任意の3要素a,b,cに対して結合法則が成立する。
   (ab)c=a(bc)
3. Gはae=ea=aなる要素eを含む。このようなeを単位元という。
4. Gの任意の要素aに対して、aa^-1=eなるようなa^-1がGに含まれる。
   a^-1をaの逆元という。

｢代数的構造｣遠山啓(ちくま学芸文庫)

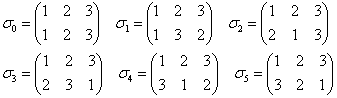
1. 合成置換は以下のようになる。確かにすべての合成結果が、σ₀〜σ₅のいずれかになっているから、1の要件はみたす。
   
2. 結合法則、ひとつだけ例を挙げてみる。
   (σ₁σ₂)σ₃=σ₃σ₃=σ₄
   σ₁(σ₂σ₃)=σ₁σ₅=σ₄
3. 単位元はσ₀である。
4. 逆元について、
   σ₀^-1=σ₀ , σ₁^-1=σ₁
   σ₂^-1=σ₂ , σ₃^-1=σ₄
   σ₄^-1=σ₃ , σ₅^-1=σ₅

「不変量と対称性」今井淳、寺尾宏明、中村博昭（ちくま学芸文庫）

• n=2
  
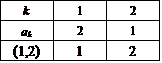
  これは互換[1,2]である。要素が2つしかないのだから、これ以外の方法がないから1通りで、もしこの互換を偶数回繰り返したら、元に戻って｢不完全順列｣になってしまうから、奇数回でなければならない。
• n=3
  
  3次の巡回置換をσ=[1,2,3]とすると、左はσ、右はσ²、である。上にあったように、これを互換の積に分解する方法は無数に、あるから、ここでルールを決める。
  本末転倒(笑)ではあるが、すでにわかっている｢完全順列｣から出発し、順次、これを自然数(順序数)の並び1,2,3に戻していく。もちろん、最小の回数で。その際、後の方の番号から順に目的に合わせていく。
  つまり、2,3,1なら、3番目を｢3｣にしたいから、まず互換[1,3]を行い、2,1,3となったから、今度は2番目を｢2｣にしたいから、互換[1,2]を行う。このようなルールに従えば、｢一意性｣が確保できると思うのだが、どうであろうか?
  
  こうして、3次の巡回置換σ=[1,2,3]は、互換[1,2]と互換[1,3]の積として、
  同じくσ²は、互換[1,2]と互換[2,3]の積として、あらわすことができることがわかった。
  
  では、どうして、3次の｢完全順列｣は2つしかないのか?
  3個の要素1,2,3の上で、互換を1回しか行わなかったら、番号と値が一致しているものがどうしても1つ残る。
  ｢完全順列｣にするには、どうしても2回は互換を行わなければならない。でも、2回目は何でもいい訳ではなくて、1回目が[1,2]、2回目も[1,2]なら、元に戻ってしまうだけだ。
  1回目と2回目とで、3個のすべての要素をカバーする、覆っている、ものでなければならない。1回目を[1,2]とするなら、2回目はからなず3を含んだ、[1,3]または[2,3]でなければならない。だから、2つなのだ!
  苦し紛れだが、説明にはなった。次にいこう。
• n=4
  上と同じルールを採用した。3,1,4,2を例にとれば、これを順次1,2,3,4に戻していくために、
  4番目を｢4｣にしたいから、互換[2,4]で、3,1,2,4、
  3番目を｢3｣にしたいから、互換[2,3]で、2,1,3,4、
  2番目を｢2｣にしたいから、互換[1,2]で、1,2,3,4、
  したがって、逆に眺めて1,2,3,4から3,1,4,2を生成する変換は、3つの互換[1,2],[2,3],[2,4]の積としてあらわされることになる。
  
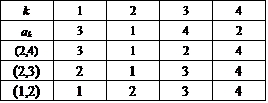
  さて、だんだんスリリングになってくるのだが(笑)、4次の｢完全順列｣は9個あった。これが、2個の互換の積であらわされるもの3個と、3個の互換の積であらわされるもの6個に、くっきりと分かれ、これがしかも、前者の方が、前回の議論で問題にした、3次の｢完全順列｣と対応できず、むしろ2次の｢完全順列｣と対応付けられるもの、に、綺麗に一致しているのだ。
  これが、2個の互換の積であらわされるもの。共通の特徴は、上から3段目の前3つの数字、つまり4だけ切り離した3次の順列が(2,1,3),(3,2,1),(1,3,2)と、いずれも番号と値が1か所一致した不完全順列であること。
  
  
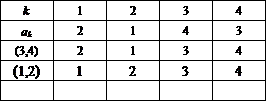
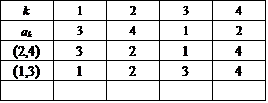
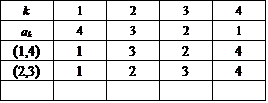
  では、どうして、このパターンの｢完全順列｣が3個なのか?、説明しなければならない。
  はじめが、[1,2],[3,4]、次が、[1,3],[2,4]、そして、[2,3],[1,4]、・・・、もうお気づきですね(笑)、これは集合{1,2,3,4}を2つの互いに素な、要素2個の部分集合に、分割する方法なのだ!
  4個から2個選べば、残り2個は決定する。その方法は₄C₂=6だが、何と興味深いことに、ここでは、連続する2つの互換が、｢交換可能｣なのである。
  一番初めのものを例にとれば、まず、集合{1,2,3,4}を2つの部分集合{1,2}と{3,4}に分ける。しかるのち、それぞれの部分集合内で、相手とは無関係に(!)、その要素の順序を入れ換えているだけなのである。だから、交換可能なのは、当たり前なのである。
  だから、₄C₂÷2!=3、というわけだ。
  
  少なくとも3個の互換の積としてしかあらわすことのできない残り6個についてみる。これらに共通の特徴はもちろん、最後尾の｢4｣だけをそろえた段階、つまり上から3段目の前3つの数字が、すべて(2,3,1),(3,1,2)と、3次の完全順列をなしていることである。
  そして、上の場合と異なり、3個の互換の間には、交換法則が成り立たない。(交換しても、いずれも完全順列を生成するのだが、6個全部をカバーしているわけでもなく、なんだか支離滅裂のように思えるから、この点にはさしあたり深入りしないことにする。)
  
  
  
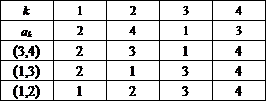
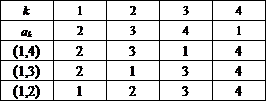
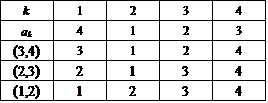
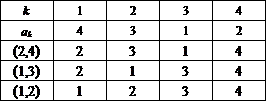
  さて、これがどうして、6個なのだ?
  集合(1,2,3,4)から、まず、(1,2)を、選ぶ。次に(3,4)という風に排反的に選んでしまうと、上のパターンと同じになってしまう。なおかつ、3という要素も、4という要素も、ちゃんと関与させないと完全順列にはならないから、
  まずは3を絡めるために、(1,2)の後は、(1,3)または(2,3)を置かなければならない。
  1. (1,2)→(1,3)
  2. (1,2)→(2,3)
  これにさらに4を絡めるには、
  1. (1,2)→(1,3)→(1,4)または、(2,4)または、(3,4)
  2. (1,2)→(2,3)→(1,4)または、(2,4)または、(3,4)
  確かに、これで6通りである。2×3=3!=6と、言えなくもないが、一般化して下の式と｢辻褄を合わせる｣方法が、わからない。
  
  
• n=5
  D(5)=44であるが、これらは、3つの異なる互換の積としてあらわすことができるもの、20個、少なくとも4つの互換の積としてしかあらわすことができないもの、24個、に分割される。
  A(4)と関連付けられるもの36個、A(3)としか関連付けられないもの8個、という先述の結果とは、それほど綺麗に符合してくれない。ただ、A(3)としか関連付けられないもの8個、は、ことごとく、3個の互換の積であらわされる20個のうちに含まれているのが｢不幸中の幸い｣(笑)であろう。
  第1グループ：3つの異なる互換の積としてあらわすことができるもの、20個、のうち、A(3)としか関連付けられないもの8個
  
  
  
  
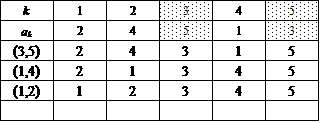
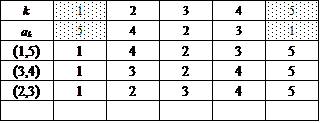
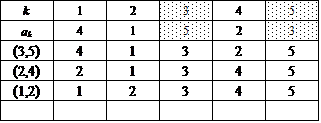
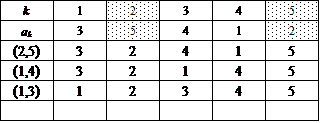
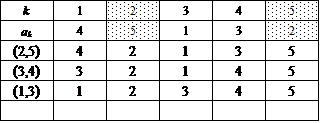
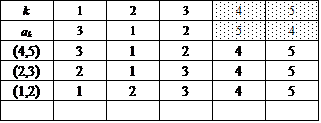
  このグループの共通点は、表を下から順に眺めていくとわかるが、集合{1,2,3,4,5}を、互いに素な(共通の要素をもたない、排反な)部分集合2つの｢直和｣に分解する際、まず、要素の個数3個のものを取り出す、すると、要素の個数2個のものが残る、という手続きを行っているらしい。
  左一番上のものを例にとると、{2,3,4},{1,5}と、分けているのである。
  集合{2,3,4}の内部では、巡回置換σ,σ²によってただ2つの完全順列を生ずることは、すでにn=3での検討でわかっている。
  では、このような部分集合への分割の仕方は何通りあるか?
  ここでは、5という要素をかならず要素2個の部分集合の方へ割り当てている。だから、{1,5},{2,5},{3,5},{4,5}の4通り。したがって、4×2=8。
  では、5以外の要素について同様の手続きをしても、同じ結果なのか?、との疑問が残るが、要素1,2,3,4,5は、いずれも特に区別することのできない、｢対等｣な要素なのであるから、たぶん、大丈夫(笑)なのであろう。
  
  第2グループ：3つの異なる互換の積としてあらわすことができるもの、20個、のうち、A(3)としか関連付けられないもの、以外の12個
  
  
  
  
  
  
  
  
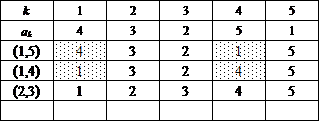
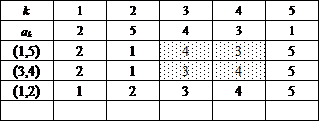
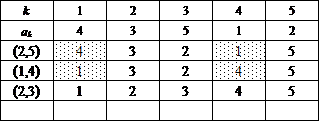
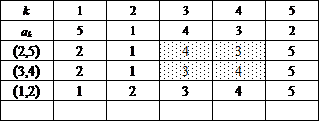
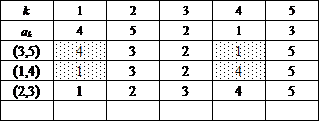
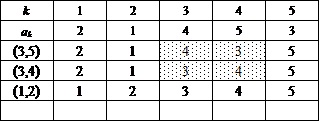
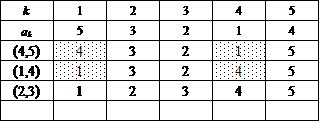
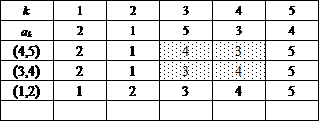
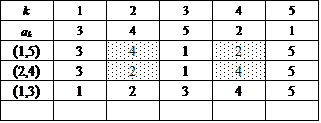
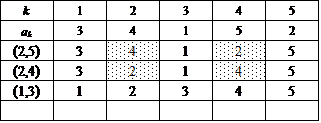
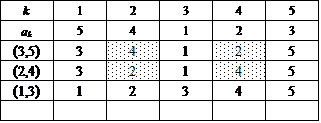
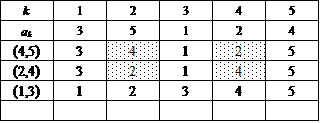
  ここでは、{1,2,3,4,5}を2つの部分集合の直和に分解するに当たって、一方をまず{5}に固定する。
  次に、集合{1,2,3,4}に関して、n=4のときにもやったように、要素2個の部分集合2つに直和分解する。
  この方法は、{1,2},{3,4}と{1,3},{2,4}と{1,4},{2,3}との3通りであった。
  これに対応して、得られた4次の完全順列3個のそれぞれに対して、今度は、[*,5](*=1,2,3,4)なる互換を施すのである。だから、3×4=12。
  
  第1グループとの間に重なり合いはないか?、大丈夫(笑)、1回の互換によって、2つの番号と値が一致してしまうようなペアは存在しないから。
  第3グループとの間に重なり合いはないか?、それは、第3グループについて見たのちに検討しよう。
  
  第3グループ:少なくとも4つの互換の積としてしかあらわすことのできないもの。
  
  
  
  
  
  
  
  
  
  
  
  
  こんどは、{1,2,3,4}と{5}に分けた。
  {1,2,3,4}を要素2個ずつの2つの部分集合に分けるのではなく、{1,2,3}と{4}と分けると、
  {1,2,3}からは、3次の巡回置換σ,σ²によって、2個の3次の完全順列が得られ、
  これに、[*,4](*=1,2,3)の互換を施せば、6個の4次の完全順列。
  さらに、[*,5](*=1,2,3,4)の互換を施して、6×4=24個の5次の完全順列。
  
  第1グループとの間に重なり合いはないか?、大丈夫(笑)、1回の互換によって、2つの番号と値が一致してしまうようなペアは存在しないから。
  第2グループとの間に重なり合いはないか?、大丈夫(笑)、互換[*,5]を施す以前の4次の完全順列が、n=4のところで見たように、
  {1,2},{3,4}型3個と、{1,2,3},{4}型6個と、すでに排反なのであるから。