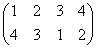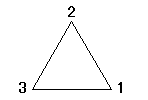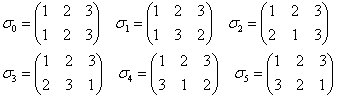集合(1,2,3,4)上の置換は、4P4=4!=24個ある。左上が「何もしない」恒等置換。
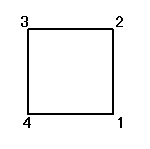
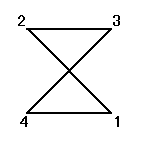
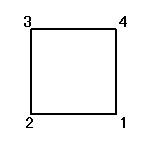
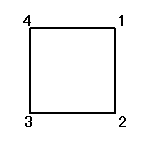
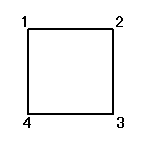
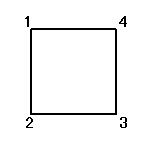
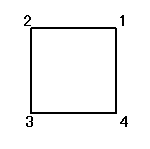
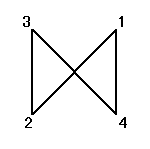
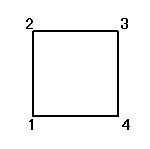
正方形をまっすぐに(笑)置き、右下から順に反時計回りに1,2,3,4と番号をつける。
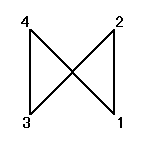
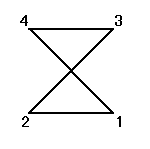
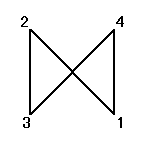
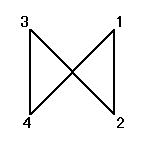
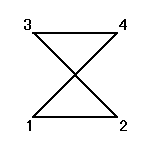
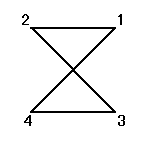
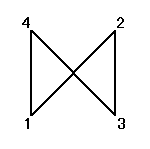
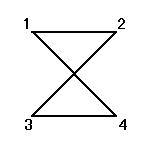
それぞれの置換によって得られる図形は、正方形、「8の字」型、「∞」型、と3種類ある。
「正方形」が、「正方形」に移される置換は、24個のうち8個だけなのである。
集合(1,2,3,4)上の巡回置換は、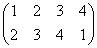 で、これをσと名付けると、
で、これをσと名付けると、
σ=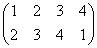 , σ2=
, σ2= , σ3=
, σ3=
で、これらはそれぞれ、正方形を時計回りに、90度ずつ、転がしていく変形を表す。もちろん、これらによって生成されるのは「完全順列」である。
正方形を、左右対称に、裏返す変形をb=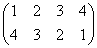 と名付けると、
と名付けると、
bσ=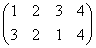 , bσ2=
, bσ2=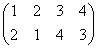 , bσ3=
, bσ3=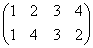
σb=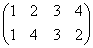 , σ2b=
, σ2b=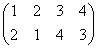 , σ3b=
, σ3b=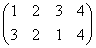
で、これらの中で「完全順列」を生ずるのは、
b=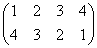 , bσ2=σ2b=
, bσ2=σ2b=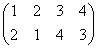
のみで、他の、
bσ=σ3b=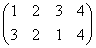 , bσ3=σb=
, bσ3=σb=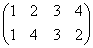
は「完全順列」を生じない。
恒等置換e=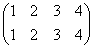 を含めて、
を含めて、
e , bσ=σ3b , bσ3=σbの3個の「不完全順列」型、
b , σ , σ2 , σ3 , bσ2=σ2bの5個の「完全順列」型、
これで、正方形を正方形に移す変換8個は、尽くされた。
4次の「完全順列」は、9個あったはずだ。ここまでで現れたのは5個、残り4個はしたがって、「8の字」型、「∞」型、に隠れさていることになる。探してみよう。
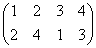
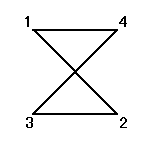 ,
, 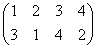
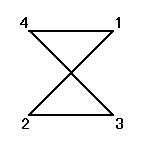
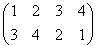
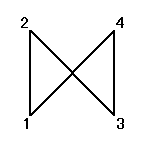 ,
, 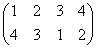
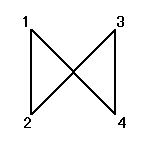
であった。
何が言いたいかというと、正三角形から、正方形へ、1増えることによって、こんなにも「複雑さ」が増してしまう。
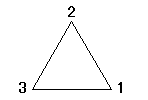
正三角形の場合なら、集合(1,2,3)上の置換は、下の6個、
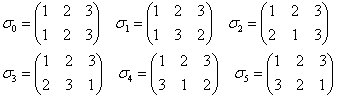
恒等置換e=σ0、巡回置換σ=σ3とすれば、σ2=σ4
左右裏返しをb=σ5とすれば、bσ=σ2b=σ2、bσ2=σb=σ1
で、全部が尽くされてしまう。
「完全順列」を生ずるのは、σ=σ3 , σ2=σ4
「不完全順列」を生ずるのは、e , b , bσ=σ2b=σ2 , bσ2=σb=σ1
である。少なくとも、正三角形が、正三角形でない(!)ものに移されてしまうことはない。
さまざまなことが連想される。正方形に比べて、正三角形は、はるかに「堅固な」構造なのである。
立体化して考えると、正四面体の方が、立方体より、はるかに「堅固」なのである。
この世で最も強固な物質はダイヤモンド、最外殻電子4個が空間的に対等に配分された4方向の共有結合によって、「正四面体」構造を作る。
「生物」の構成要素が、同じく炭素を中心原子とするアミノ酸であり、「無生物」たる鉱物のほとんどが、同じく最外殻電子4個のケイ素を中心原子とするケイ酸塩であることは、もちろん偶然ではない。
「古代人」は、3本のまっすぐな木材を探してきて同じ長さに切り、その一端を、何か蔓性の植物でくくって「三脚」を作り、3個の他端を地面の上に「正三角形」になるように置いて、「正四面体」型の住居を作った筈だ。
「立方体」のアパートメントブロックは、「強度」の要請によるものではなく、「空間の有効利用」という「経済合理性」が動機である。
「立方体」は、「ずれ」や「ねじり」の力に、きわめて弱いのである。まさに、ここでのように、正方形が正方形でないもの、「8の字」型や、「∞」型に、変形してしまうからなのである。
四脚の椅子やテーブルは、作りが悪かったり老朽化すると、がたがたしますね。なぜでしょう?
2次元平面は、2個の1次独立ベクトルの1次結合として、十全に構成される。つまり、同一直線上にない3点によって、平面は、ただ一つに「決定」されるからです。第4点目が、同じ平面上にある保証がない。だから、「三脚」は安定なのに、四脚は不安定なのだね。
同様に、3次元空間は、3個の1次独立ベクトルの1次結合として、十全に構成される。正四面体の6辺のうち、どの3辺も1次独立であるが、立方体のどれか1点を始点として、そこから発する3辺を1次独立ベクトルとして選ぶと、これで4頂点使ったから、残り4頂点は、これらの1次独立ベクトルの1次結合として表現されてしまう、1次従属な点なのである。「従属性」をはらむことが、構造的な「弱さ」に対応する。
ビリヤードのボールのような、同じ大きさの堅固な球体を、なるべく密に詰めることを考えましょう。スーパーマーケットの卵のパッケージの並べ方が参考になりますが、・・・、同一平面内では、3個の球の中心が、「正三角形」になるようにし、その上の段には、正三角形の重心の上空にもう一つの球の中心が来るようにし、こうして「正四面体」ユニットができます。
これが、六方最密充填、あるいは、少し並べ方がずれるのだが、面心立方格子と呼ばれる金属結晶の「最密構造」で、
そのうちの六方最密充填にならうなら、最下段に正六角形状に6個のボールを配し、その上の段には、隙間に3個を正三角形上に並べ、次の段はまた最下段と同じ正六角形で、を繰り返して、正六角柱を作っていけば、最密構造が得られるのであるが、・・・、
「コアラのマーチ」ってお菓子、今でもありますか?、あれ、正六角柱でしょ?、でも、誰もがあのパッケージ採用しないのは、やはり、「立方体」基準の「経済合理性」に反するからです。直方体のダンボールに「コアラのマーチ」詰めたら、隅に隙間ができるでしょ?
でも、実は(笑)、卵でもキャベツでも、たまねぎでも、「自然」が生み出したものは、「エルゴード性」が生み出した、まったき「無方向性」、すなわち球体、これはミクロな正四面体構造の集合なのだが、・・・、なのだから、これを立方体のダンボールに、詰めようとする、方が、間違っている(笑)、とも言えるのです。
「世界」は、「正四面体」の「自然」と、「立方体」の「文明」=「資本主義」(笑)との闘いなのである、などという妄想を弄んでみましょう(笑)。
それは、自然数列上の、「3」と「4」との、超えがたい差異に根拠をもっている。最初の偶数の素数「2」と、最初の奇数の素数「3」で起ったことが、全然「4」では再現されない。「4」以降のすべては、きっと「2」と「3」の組み合わせに「還元」できる。
やはり「2」と「3」は、特別な数なのである、「コラッツ予想」のところでお話したような、「神秘主義」(笑)が、ここでも顔を出します。
あ、もう一つ付け加えておこう。平面図形の中で、ただ一つ「対角線」ともたない図形が三角形、
空間図形の中で、ただ一つ「対角線」をもたない立体が四面体、です。
これが、平面の区画を、隣接区画は同じ色にしてはいけない、というルールで塗り分ける、「4色問題」と、対応関係を有しているらしいことは、すでに述べました。
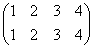
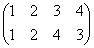
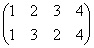
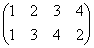
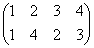
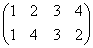
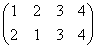
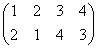
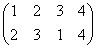
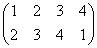

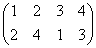

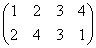
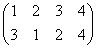
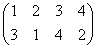

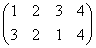
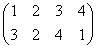

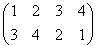


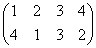
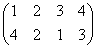
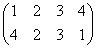
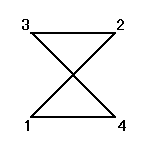
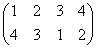

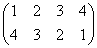
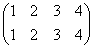

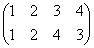

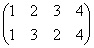

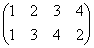

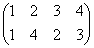

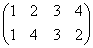

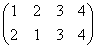

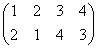

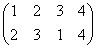

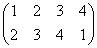

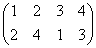

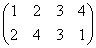

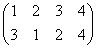

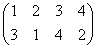

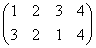

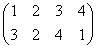



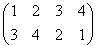



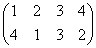

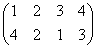

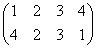
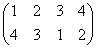

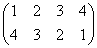

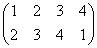 で、これをσと名付けると、
で、これをσと名付けると、
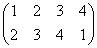 , σ2=
, σ2= , σ3=
, σ3=
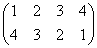 と名付けると、
と名付けると、
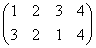 , bσ2=
, bσ2=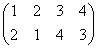 , bσ3=
, bσ3=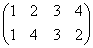
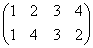 , σ2b=
, σ2b=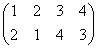 , σ3b=
, σ3b=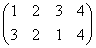
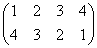 , bσ2=σ2b=
, bσ2=σ2b=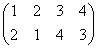
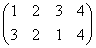 , bσ3=σb=
, bσ3=σb=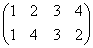
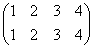 を含めて、
を含めて、
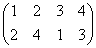
 ,
, 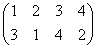

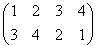
 ,
,