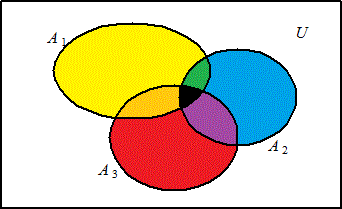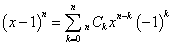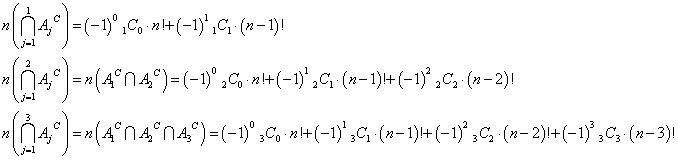数理統計学の教科書をぱらぱらと見ていたら、完全順列の個数の求め方が、こともなげ(笑)に出ていた。もっとも、これは証明にはなっていなくて、帰納的な類推に過ぎず、では、そのあとを数学的帰納法で証明すればよいではないか?、とやりはじめて見たが、頓挫した(笑)。｢類推｣の場面まで、紹介する。

---

｢1｣から｢n｣までの自然数が書かれたカードを左から順に並べていく。左から順に第1位、第2位、・・・、という具合に名付けることにする。
第k位までのカードの数字が、kに一致しているような並べ方の方法全体の集合をA_kと称する。

• A₁・・・第1位の数字が一致している並べ方。第1位以外の数字に関しては、一致しようがしまいが、関心はない。
  第1位に｢1｣を配し、他はどうでもよいから、その個数、n(A₁)=(n-1)!
• A₁^C・・・その補集合。全体集合Uの要素の個数はn(U)=n!だから、
  n(A₁^C)=n(U)-n(A₁)=n!-(n-1)!  ・・・  (ア)
• 同様に、n(A₂)=(n-1)!  ,  n(A₃)=(n-1)!
• 次に、A₁∩A₂は？・・・第1位および第2位が一致、他はどうでもいいから、n(A₁∩A₂)=(n-2)!
• 同様に、n(A₁∩A₃)=(n-2)!  ,  n(A₂∩A₃)=(n-2)!
• では、A₁^C∩A₂^Cは？・・・｢ド・モルガンの法則｣より、A₁^C∩A₂^C=(A₁∪A₂)^C
  n(A₁^C∩A₂^C)=n((A₁∪A₂)^C)=n(U)-n(A₁∪A₂)=n(U)-{n(A₁)+n(A₂)-n(A₁∩A₂)}
  
  すなわち、
  n(A₁^C∩A₂^C)=n!-{(n-1)!+(n-1)!-(n-2)!}=n!-2(n-1)!+(n-2)!  ・・・  (イ)
• では、A₁^C∩A₂^C∩A₃^Cは？・・・｢ド・モルガンの法則｣より、A₁^C∩A₂^C∩A₃^C=(A₁∪A₂∪A₃)^C
  n(A₁^C∩A₂^C∩A₃^C)=n((A₁∪A₂∪A₃)^C)=n(U)-n(A₁∪A₂∪A₃)
        =n(U)-{n(A₁)+n(A₂)+n(A₃)-n(A₁∩A₂)-n(A₁∩A₃)-n(A₂∩A₃)+n(A₁∩A₂∩A₃)}
  
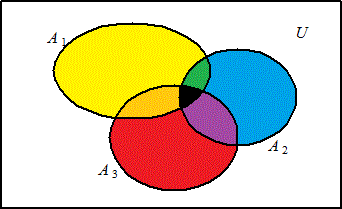
  すなわち、
  n(A₁^C∩A₂^C∩A₃^C)=n!-{(n-1)!+(n-1)!+(n-1)!-(n-2)!-(n-2)!-(n-2)!+(n-3)!}
        =n!-3(n-1)!+3(n-2)!-(n-3)!  ・・・  (ウ)
• (ア)(イ)(ウ)3式の係数を見て気づくのは、二項係数、(x-1)ⁿの展開式の係数であることだ。
  
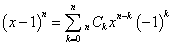
  そこで、こう類推する。
  
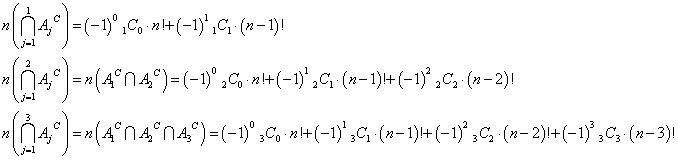
  であったから、