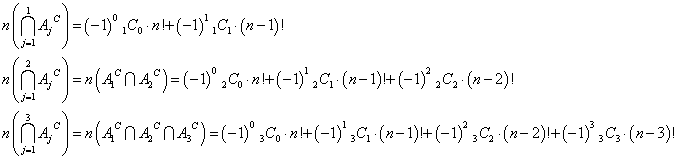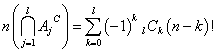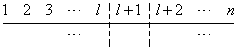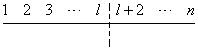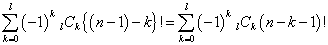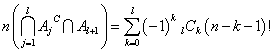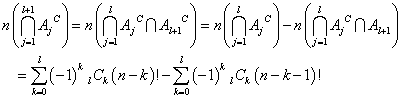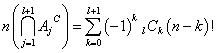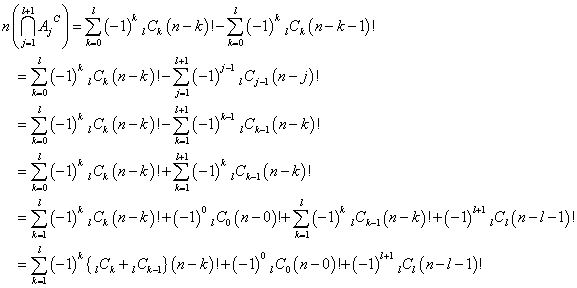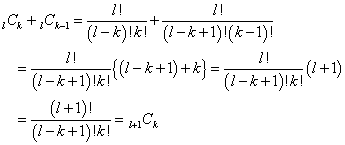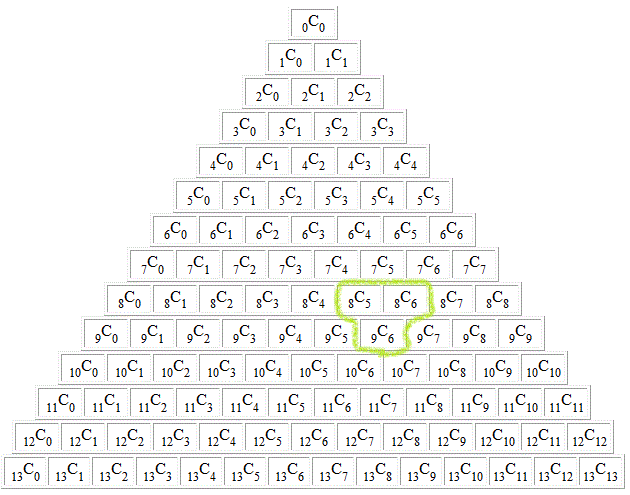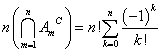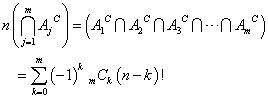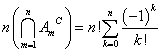
の、「数学的帰納法」による証明、うまくいったので(笑)、ご報告申し上げます。
何を以て、「仮定」とするのかが、悩ましい。上式は、n次の完全順列の個数、なのであるが、そのnについての帰納法なら、
D(n+2)=(n+1){D(n+1)+D(n)}
であることは既にわかっているのだから、直前の項だけではなく、そのひとつ前も考慮しなくてはならない、n=1,2を証明し、n=k及びn=k+1を仮定して、n=k+2を導く、という二段階の帰納法になるはずだが、そうすれば、ここまでの議論をもう一度「蒸し返す」だけで、ここでは、そうではなく、漸化式ではなく、直接に上の式を導きたいのである。
上の式を「類推」した根拠は、こうであった。
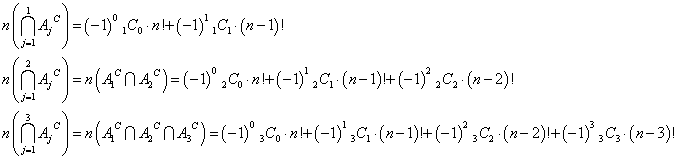
1,2,3,・・・,nが記されたカードが一枚ずつあり、それを左から順に並べていく際、
一番左n=1だけは一致していない、それ以外はどうでもいい、
左から一番目と二番目n=1,2だけは一致していない、それ以外はどうでもいい、
左から一番目と二番目と三番目n=1,2,3だけは一致していない、それ以外はどうでもいい、
・・・、そこまでが、確認できたのである。
当然、左から一番目と二番目と三番目と・・・m番目まで、n=1,2,3,・・・,mだけは一致していないが、それ以外はどうでもいい、ような並べ方の個数が、
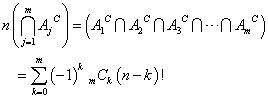
であることを、自然数mについての帰納法として、証明することになる。早速はじめよう。
1,2,3,・・・,nが記されたカードが一枚ずつあり、それを左から順に並べていく際、
左から数えて一番目と二番目と三番目と・・・m番目までのカードに書かれた数字が、左から数えた番号n=1,2,3,・・・,mに一致していないが、それ以外のm+1番からn番までは、一致していてもしていなくてもどうでもよい、ような並べ方の個数が、
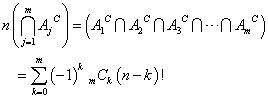
とあらわされることを示したい。ここに、Ajとは、第j番目が一致している、他についてはどうでもよい、場合の数を表している。
- m=1,2,3については、以下のように、この式が成立していることが示される。
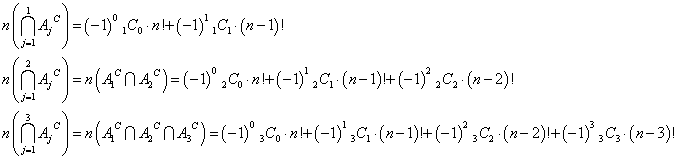
- m=lのとき、この式が成立すると仮定する。すなわち、
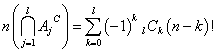
ここで、一番目からl番目は一致していない配列に対して、l+1番目の一致不一致を考慮するには、次の二種を区分しなければならないことに気づく。
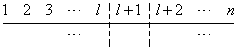
- 一番目からl番目までに、既に数字l+1が用いられている場合
- l+1番目からn番目のどこかに、数字l+1が用いられている場合
前者の場合は、l+1番目に数字l+1が用いられる心配は一切ない。
後者については、l+1番目に数字l+1が用いられている可能性が含まれている。
そこでこんな技巧を施す。上の段の番号l+1、下の段のどこにあるかわからないが数字l+1をともに削除する。
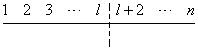
その個数は、番号1,2,3,・・・,l,l+2,・・・,nと、一つだけ飛んだn-1個の数字から、l個選んで左から並べたところ、一番目からl番目までは一切一致していなかった、という配列の個数、
であるから、「仮定」に従えば、
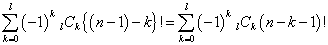
となるではないか?、そこにふたたび「こっそり」(笑)上段にも下段にもl+1を差し込むのである。それによってもちろん、個数は増えも減りもしない。

この配列は何を意味しているか?、一番目からl番目までは一つも一致していない、かつ、l+1番目は一致している、それ以降は、どうでもいい、という配列の個数なのである。
つまり、
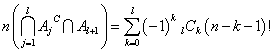

これで準備は整った。
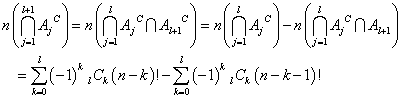
この式の右辺が、めでたく、
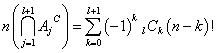
となることを、願うばかりである(笑)。
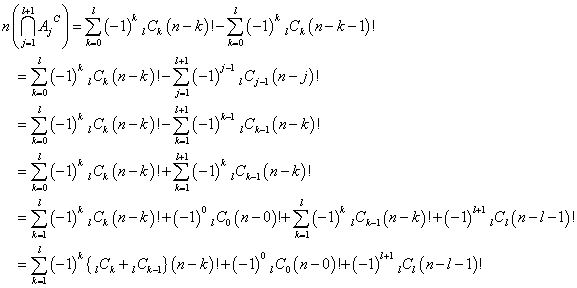
j=k+1なる変数変換を施したのち、ふたたび、jをkに戻した。二つのシグマ記号の始期と終期がずれたので、共通しているk=1から、k=lまでをまとめて、端数部分を外に出した。
ここで、
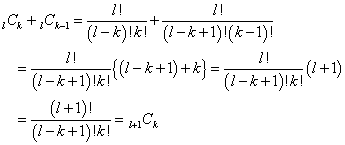
視覚的にわかりやすくいうと(笑)、「パスカルの三角形」で、同じ段の隣接2項を足せば、その下の段の真ん中の項になる、理屈。
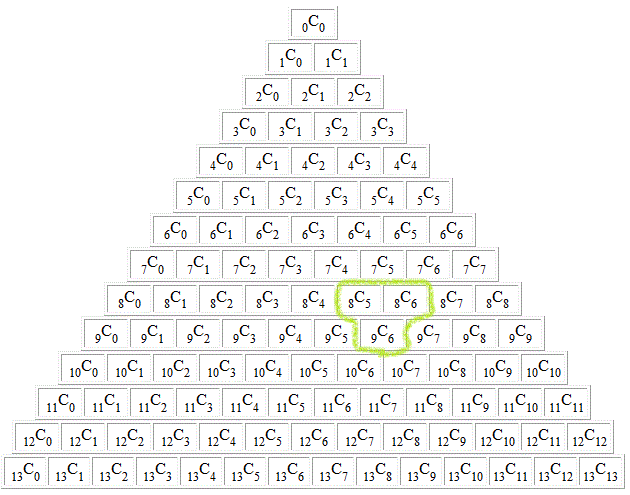
よって、

m=l+1のときも成立する。
以上から、m=1,2,3,・・・,nに対して、
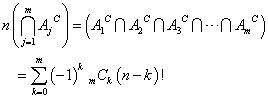
が成立する。よって、
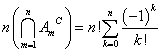
である。