ネイピア数eは、
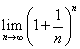ないしは、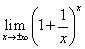
の極限値として定義される。円周率は、言うまでもなく(笑)円周の長さと直径の比、で、これら二つの数は、いずれも、「超越数」、いかなる代数方程式、整数係数のn次多項式を等号で結んで0としたもの、・・・、等式は両辺を同じ数で割っても差し支えないから、これは有理係数のn次多項式を等号で結んで0としたもの、と言ってもいい、の解には決してならない数、であることが知られている。
虚数単位iは、2次方程式ax2+bx+c=0の、「解の判別式」D=b2-4acが、負になっても、なお解がある、と強弁するために、「発明」された。自然数の集合は、加法と乗法については「閉じている」が、減法についても閉じているようにしたければ、小さなものから大きなものを引いた結果は、大きなものから小さなものを引いた結果にある記号を付して、区別しなければならなかった。ここから、自然数、「名付けうるもの」を順に数える順序数、数え終わって、既に順番を忘却してしまった、「カーディナル数」、あわせて「自然数」に、0、と負号「-」を付した自然数を合わせて、「整数」が登場したのである。
これら４つの、極めて「人為的」な数が、こうして「一堂に会して」いる様は、その発見者たちにとっても、やはり「不気味な」符合だったのであろう。だから「人類の至宝」なのである。「私たち」は、そんなに大したことをしなかった。「世界」は依然として、絶望に満ちている。「言語」によって長期記憶を獲得できたからといって、出来たことは、せいぜい、これぐらいのことなのである。私は(笑)もうじき去るから、この人類の「達成」を、腹蔵なく祝福することがまだ(笑)、できる。
先を急ごう。ex、sinx、cosx、の、マクローリン級数展開を行う。
では、「マクローリン級数展開」とはなんであったか?
xのn次多項式f(x)の各係数anは、以下のように、f(x)を順次微分して、0を代入することによって、得ることができる。
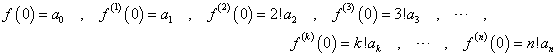
すなわち、
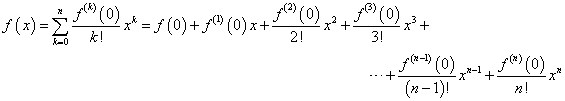
ならば、無限回微分可能な関数g(x)に対しては、これを用いて、xのn次多項式による近似が可能であることがわかる。第n次で止めてしまうと、そこに誤差が生じこれを「剰余項」と呼ぶのだが、そこの詳しい話には立ち入・れ・な・い・、ので、nをどんどん大きくすれば、どんどん真の値に近づくでしょ?、という雑な話で流しておく。
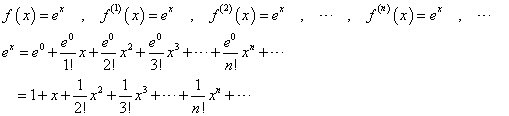
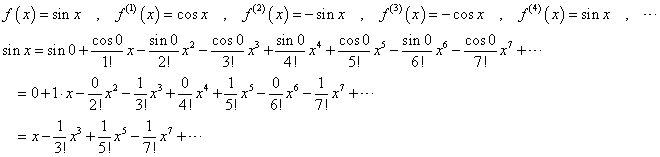
ここで話を複素関数にまで広げる。微分係数というものを、平均変化率の極限、というだけでは、その複素平面上での「意味」を説明することはできない。本当にできないのか、私が無能だからできないだけなのかは、知らない(笑)。目標は、eiθ=cosθ+isinθという等式が、無限級数に展開した形において、ほら、「・・・」のところもことごとく一致しているではないか？、と、強弁するところにある。虚数単位iなるものも、微分の扱いとしては、単なる定数であって、二回かければ、「-1」になるだろ？、ということで、淡々と(笑)、話を進める。
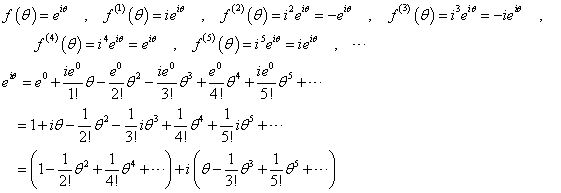
ほら、この式の実数部は、cosθの級数展開、虚数部は、sinθの級数展開に、一致していそ・う・だろ？、従って、eiθ=cosθ+isinθ、これが「オイラーの公式」と呼ばれるもので、確かに、θ=πを代入してみれば、eiπ=-1が得られるわけである。