そんなに、簡単な話ではなさそうなのだ。まず、私たちは、もう何世紀も前に、大論争の末、「地動説」を受け入れたはずなのだが、依然として、「客観的な観測者」たる自分が立っている場所が、「世界」の中心である、という想念、いわばcentrismから、決して自由になれないらしいのである。地球は太陽の周りを回っている。よかろう、では、月は？、太陽を中心としてほぼ円軌道を描いて公転している、その地球を「中心」として、回っている、と、考えてしまいがちだが、現に私も考えていたが、・・・、そこから離れないと、この話は決して理解できないようなのである。
太陽、地球、月、三つの天体が、相互に万有引力を及ぼし合いながら運動する。これは「三体問題」と言われるもので、既にして厳密な微分方程式を立ててそれを解くことが不可能であることが知られている。だから、例えば太陽・地球関係を問題にするときは、月のことを無視し、地球・月関係を考えるときは、太陽の事を忘れる、といった「近似」を導入せざるを得ない。
「作用・反作用の法則」と呼ばれるものがあり、力というのは、必ず、相互的に及ぼされる、AがBを引いた、というのなら、かならずBもまた、Aを引いているのである。物理の教師が、黒板消しを目の前で落として見せて、「ほら、これは、地球が黒板消しを引っ張ったように見えるけど、黒板消しもまた地球を引いているんだよ」などといっても、あまり説得力はないが、それは、地球と黒板消しの質量比があまりにも大きいから、黒板消しは「吹けば飛ぶように」動くけれど、同じ大きさの逆向きの力を受けても、地球は微動だにしないから、地球を「固定した」座標原点とみなしてよいことを意味している。
どの座標系が「絶対的」であるかを、特定することは、決してできない、というのが、「・・・はできない」という「発見」ずくめの、だからこそ、「努力すれば、なんでもできる」(笑)なる「近代」の確信の凋落をいたるところから証立ててくれたという意味で「ポスト・モダン」であった前世紀初頭の、・・・、「相対論」の粗雑な要約である。
太陽・地球関係では、依然として太陽の質量が、圧倒的に地球の質量を凌駕しているから、「公転」の中心は、太陽の中心そのもの、つまり、太陽は「動いていない」と確言して差し支えない、のに対して、どうやら、地球と月との関係は、半径の比が、約4:1、質量比が、その3乗で64:1と思いきや、約80:1、どうも、月の方がやや密度が小さいと見える、・・・、いずれにしてもそんなに「べらぼうな」比ではなく、地球が月を引けば、月もまた地球を引く、それを「考慮しなければならない」レベルなのである。
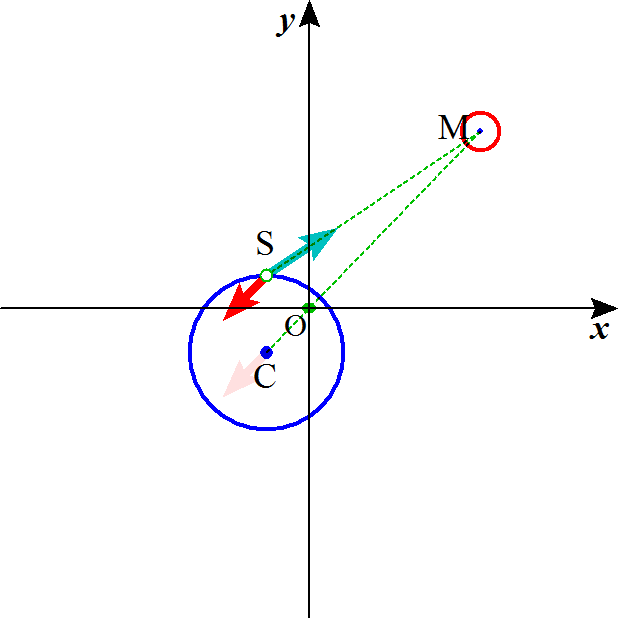
上の図は、地球・月関係の模式図である。地球と月との半径の比は正しく描かれている。地球と月との距離は、デタラメ、本当は、地球の半径の60倍くらいある、そんな絵は描けないから、思い切り縮小してある。お互いを「無視」できるような関係ではない以上、万有引力は相互的に作用するから、「公転」の中心は、地球の中心ではなくなってしまう。地球・月間の距離、を質量比80:1の逆比で内分した点が、「地球・月」系の重心であり、そこが回転中心となる。約40万キロ、80+1で割り切れるように恣意的に405000kmとしておくと、公転の中心Oは、地球の中心Cから、月へ向かって5000km、これは、地球の半径6400kmの約3/4に当たる。
竹串の両はしに、大きさの異なるお団子二つ、竹串のどこかに糸をくくりつけ、吊り下げて釣り合うようにしたい、と思っても、残念ながら、ここでは釣り合いの位置が、大きなお団子の中にあることになるから、この分かりやすい例え話は破綻するのだが(笑)、・・・、そんな感じだ。
図のC点は、centerのつもりで、地球の中心、そこから月に向かって5000キロずれたO点が、地球と月、という二つの物体でできた「系（システム）」の重心である。
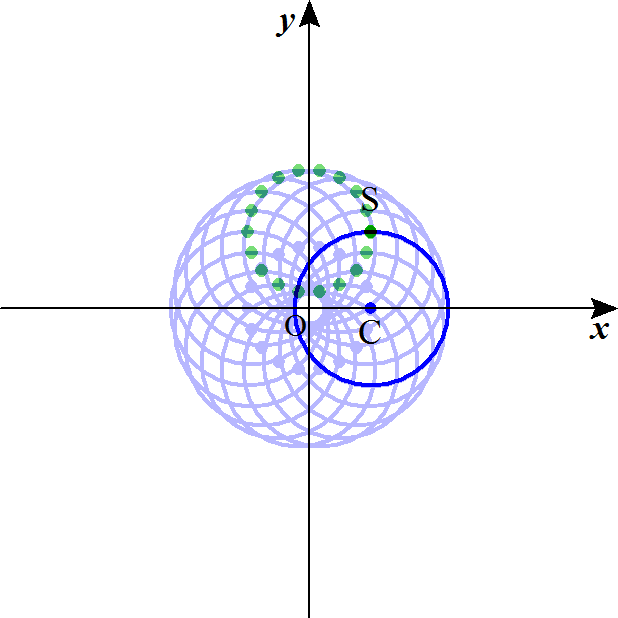
本当は、地球は自転している。しかも、月の公転よりかなり速く。ほぼ一日に一度、月が登り、月が沈む、それが私たちの実感を形作っているから、なかなか想像しがたいが、ここでは、自転していない、と、考える。図中、S点はsurfaceのつもりで、地表面上のある一点である。y座標が最大の、Cの真上にある点とした。地球は自転し・な・い・のだから、今からこれが「系」の重心、Oのまわりを回るのであるが、円盤自身をCまわりに回転させてはならない、SはつねにCの真上にあるのである。すると下図のように、CがOを中心に描いた円形の軌跡、ちょっと見にくいが、薄いブルーのドットが並んでいる、それと全く半径が同じ円が、少し上方に、緑色のドットのつながりとして描かれている、これが、S点の軌跡なのである。
「遠心力」というのは、糸に繋がれがボールをくるくる回すときのように、ボールに回転を生じさせている、すなわち、加速度を生じさせている力は、糸の張力、糸によってボールが中心に向かって引かれる「向心力」であるところ、ボールに乗っかって（！）、ボールと同じ加速度を持って、動いている観測者にとっては、ボールは「動いていない」はずだから、加速度は生じていない、運動方程式の加速度項は、ゼロでなければならない。
- 絶対的な、静止した「原点」から観測された運動方程式、
F=mrω2
糸の張力Fという「向心力」を受けて、質量mのボールに、rω2という大きさの「加速度」が生じた、と読む。rは回転半径、ωは角速度である。 - これを、加速度項をもたない運動方程式、つまり「釣り合いの式」にしたければ、・・・、右辺のmrω2を左辺に移項して、
F-mrω2=0
糸の張力と、もう一つmrω2という力が加わっているのだが、これが反対向きで大きさ同じだから、ちょうど釣り合って、だから加速度は生じない、と読む。これが「慣性力」という一つの解釈の技法で、ここで現れたmrω2なる「力」を、「遠心力」と呼ぶ。
そこで、今の、自転しない地球・モデル、に戻ると、地表面上の任意の一点は、中心はそれぞれに異なるが、すべて同じ半径の円軌道を、同じ時間をかけて回転する。mrω2の式を見ればわかるように、質量mの物体にかかる「遠心力」は、回転半径と、角速度のみで決まる。一周するのにかかる時間、「周期」は、2πを「角速度」で割ったものだから、回転半径と周期で決まる、と言ってもよい。つまり、にわかには理解しがたい結論だが、地表面上どこでも、いや、地球の内部のどの点でも、・・・、「遠心力」は、その大きさも方向も、つまり「ベクトル的」に、同・じ・、なのだ。
上に述べた、運動方程式、釣り合いの式、といった議論は、「質点の力学」のもので、大きさのある物体については適用できない。適用できる唯一の場所が、地球の中心Cである。ここに存在する質量mの物体（質点）には、月の引力と、それとちょうど釣り合う遠心力が作用していなければならない。その大きさは、
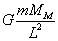、MMは月の質量、Lは、月と地球の中心間の距離、Gは、万有引力定数。
一番上の図の、ピンク色の矢印が、それである。そして、これと全く同じ力、つまり平行で同じ大きさの矢印が、地表面のあらゆる地点、もちろんSにも作用している。ところが、これが、月の引力と釣り合っているのは、唯一、地球の中心C点のみであって、それ以外の点ではことごとく、「釣り合っていない」。今、質量mの物体なるものを、「海水」の塊、と考えれば、これで、潮汐が、説明できる、というわけである。
月からの引力、それは、万有引力の式にしたがうから、距離の二乗に反比例する。一番上の図の、緑の矢印。地球と月の中心を結ぶ線上にない地点では、傾く。それに対して、「遠心力」はどこでも同じなのである。一番上の図では、赤色の矢印。これら二つの力の「ベクトル和」が、潮汐を生ずる力、「起潮力」と呼ばれるものらしいのである。
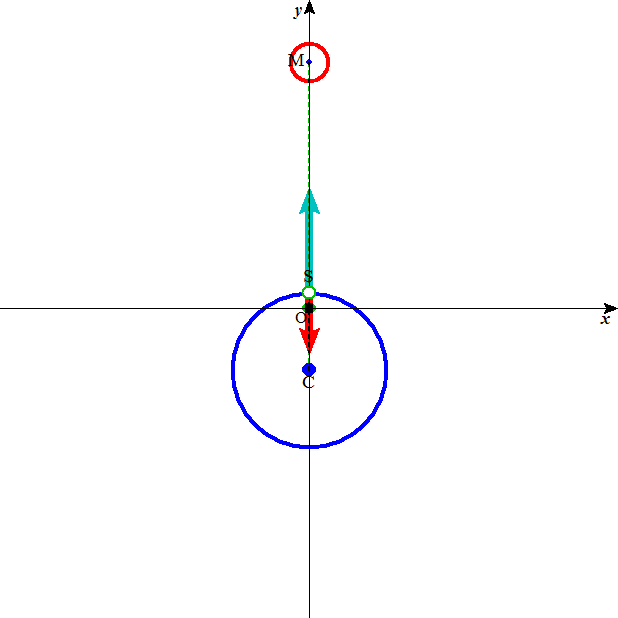
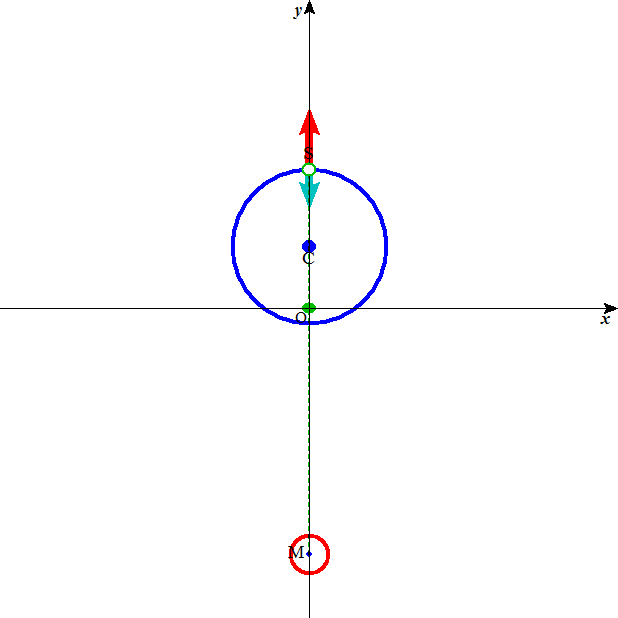
左は、月が「南中」している時、月の引力（緑色）が遠心力（赤色）と反対向きに並んでいるが、月への距離が近いので、引力が卓越しているから、全体として、海水は持ち上げられるだろう。
右は、ちょうど地球の裏側で月が「南中している」。距離が離れた分だけ、引力は小さくなるから、今度は、遠心力が卓越し、やはり、海水は持ち上げられる。
これらが、一日に二度、およそ反日を隔てた、「満潮」なのである。
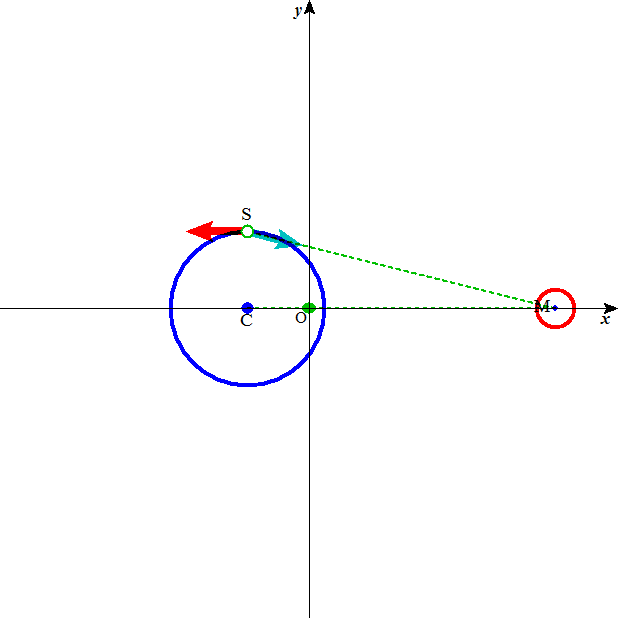
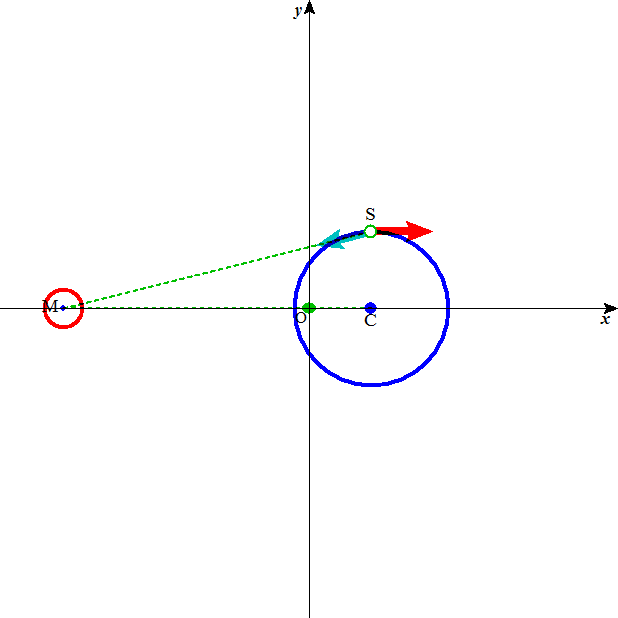
月の出、月の入りの時刻には、このように、引力と遠心力、二つの力はほぼ釣り合っており、少なくとも、海水を持ち上げるようには作用しない。これが「干潮」。
以下の大雑把な数値を用いて、計算してみた。それぞれ、ME:地球の質量、MM:月の質量、RE:地球の半径、RM:月の半径、g:重力加速度、G:万有引力定数。
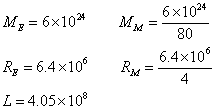
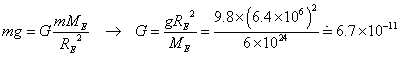
グラフの横軸は、月が南中時にある時を起点として、角度10度ずつ動かしていった時の、月の引力、遠心力の、法線方向成分を計算した。それらを足し算した結果、緑の線は、確かに、両端と真ん中、二つのピークを持っている。
バグがありそうな気もするが、とりあえず、望み通りの結果が得られたので(笑)、満足することにする。
