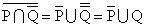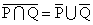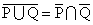「論理学入門」丹治信春(ちくま学芸文庫)という本が出まして、これが、ちょっと、「寝食を忘れる」ほど、面白い、「面白い」ことが書いてあるわけではない、もともとが、大学の教科書の文庫化なのだが、練習問題の解答が、「容易であるから各自試みられたい」みたいなのではなく、ちゃんと丁寧に掲載されていて、ノートに式を書いてみる、「答え合わせ」をする、あっていると、「嬉しい」、間違っていると、「悔しい」(笑)、そんな懐かしい、幼稚な作業に、時を忘れることが出来る。時を忘れることが出来るのは、例えば、ここに出てくる記号の羅列、
(∀x)(Fx→[(∃y)Gxy∨Gax])
などというものが、「現実世界」に、たぶん、何の対応物も持たないものであるからこそ、「屈託なく」もてあそぶことができる、本当は、「世界」は「屈託」だらけだから、それにちゃんと直面していたら、30分もすれば、へとへとに疲れて息切れしてしまうものなのに。
そういえば思い出した、80年代末葉、「ポスト・モダン」全盛の時代、ダグラス・ホフスタッター「ゲーデル・エッシャー・バッハ」が大流行で、さりげなく(笑)引用して見せるくらいの才覚がないと、「生きている価値がない」、みたいな時代だった、・・・、私も無理をして読んだ、大阪梅田の阪神百貨店で、M.C.エッシャーの展覧会があると聞けば、出向き、「バブル・エコノミー」の恩恵は、こんな下流の者にも少しは及んでいたから、高価な図録を、ぽーんと購入し、まだ物珍しかったCDプレーヤーと、グレン・グールドのバッハ全集、これまた、ぽーんと購入し、ところが残念なことに、同書の後半3分の1くらいは、「不完全性定理」の証明の紹介にあてられていて、上に挙げた如き「論理式」の、もっと激しく複雑なものが、延々と並んでいるのである。こればかりは、多少の「お金」では解決がつかない、何かを購入したとして、「わかったふり」をすることができない代物だったのですな。その、およそ30年ばかり背負い続けてきた「敗北感」(笑)を、人生も「終わり」が見えた今、「雪辱」しようとでもいうのか?
「論理学」は、大きくi命題論理、とii述語論理、に分けられる。
- 命題論理では、
- 命題変項:p,q,r,・・・
- 論理結合子:¬、∧、∨、→
- ¬:「否定」
- ∧:「かつ」、「連言」と呼ばれ、A∧Bの、A,Bを「連言枝」と称す。
- ∨:「または」、「選言」と呼ばれ、A∨Bの、A,Bを「選言枝」と称す。
- →:「ならば」、「条件法」と呼ばれ、A→Bの、Aを「前件」、Bを「後件」と称す。
からなる論理式の真偽を問題にする。
- 述語論理では、
- 論理結合子:¬、∧、∨、→
- 量化子:∀、∃
- ∀:「すべての〜、任意の〜、〜にかかわらず」、「普遍量化子」。
- ∃:「ある〜、〜が少なくとも一つ存在する」、「存在量化子」。
- 個体変項:x,y,z,・・・
- 個体パラメータ:a,b,c,・・・
- n項述語記号:F,G,H,・・・
からなる論理式の真偽を問題にする。
この書物の眼目は、「タブロー」、フランス語、英語のtableに対応する、「絵、表」のごとき意味、と呼ばれる、背理法(帰謬法)に基づく証明手続きにあるようで、私はまだ読み終えていない、今、述語論理にやっと差し掛かったばかり、読み終えた部分について、順次、わかる範囲で(笑)、紹介していく。
まずは、命題論理について、ある論理式が、命題変項に何を代入しても、常に「真」だと言える、これを「トートロジー」と呼ぶ、常に正しいから、言っても仕方ない事柄(笑)である、なのか?、もしくは、そうではなくて、命題変項の選び方次第では、「偽」となる場合が生じる、これを「矛盾」と称す、「トートロジー」が、当たり前過ぎて言っても仕方ないこと、とすれば、「矛盾」こそが、言う「価値」が存する、ことになる、などというお話は以前もしたが、与えられた論理式に対して、これを解きほぐし、「トートロジー」であるか「矛盾」であるかを判定できる方法があるようなのである。
だが、今日は、急速に眠くなってきたので、次回期待。
前回さっそく間違ったことを言った。それぞれの命題変項は、「真」か「偽」のどちらか一方の値しかとりえない。どちらでもある、とか、どちらでもない、ということはない。何を入力しても、0または1の値を返す、二値関数であるから、
- 「トートロジー」とは、用いられたすべての命題変項が、「真/偽」いずれの値をとった場合にも、ということは、n個の命題変項が用いられていたなら、2n通りの場合がありうるが、そのいずれの場合においても、「真」という「真理値」を返す命題のことであり、
- では、「矛盾」とは、用いられたすべての命題変項が、「真/偽」いずれの値をとった場合にも、「偽」という「真理値」を返す命題のことである、
と、言わねばならなかった。こうして自分で文章を作ってみると、はっきり理解していなかったこと、あいまいなままに放っておかれていたものが、次々と「露見」する。それが文章を書くことの「効用」である。もはや「還暦」近い失業者には(笑)、その「効用」を、「次回」への「投資」として役立てる機会は、ないのであるが、・・・。
それぞれの「論理結合子」に対する「真理表」を作ることから始める。「否定¬」のみは、ただ一つの論理変項の前に置かれるが、それ以外の、「連言∧」、「選言∨」、「条件法→」はいずれも、二つの論理変項の間に置かれるから、「否定」に関しては、21=2で2通り、「連言」、「選言」、「条件法」では、22=4通りのありうるすべての場合について、返される「真理値」、「真」または「偽」の二値を示す表のことである。
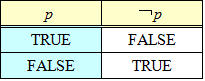
- 「否定¬」の真理表
pが「真」ならば、¬pは「偽」であり、pが「偽」ならば、¬pは「真」である、当たり前すぎることを言っている。
舞台裏を明かすと、Excelまたはその類似品(笑)には、ちゃんと「真理関数」が用意されていて、例えばセル番地が以下のようなものだったとしたら、セルに実際に書き込んでいるのは、次のようなものである。「=」で始まる文は、「関数」とみなされ、その「値」が表示される。
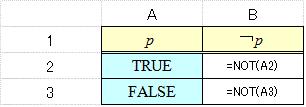
「否定¬」に対応する「真理関数」は「NOT(セル番地)」で、例えばセルB2には、セルA2に書かれている「真理値」が、「TRUE」であれば、「FALSE」を、「FALSE」であれば、「TRUE」を、返せ、と言っている。
- 「連言∧(かつ)」、「選言∨(または)」、「条件法→(ならば)」の真理表
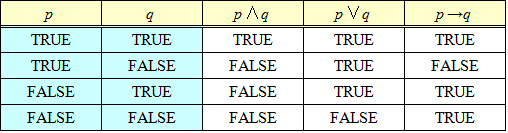
「連言∧(かつ)」では、p,qいずれもが「真」であるときの・み・、「真」であり、「選言∨(または)」では、p,qのうち少なくとも一方が「真」でありさ・え・すれば、「真」である。
議論の余地が多々あるのは、もちろん、「条件法→(ならば)」の「真理表」である。
- 命題p→qが「偽」となるのは、「前件」pが「真」であるのに、「後件」qが「偽」であるときに限・ら・れ・る・。
- 「前件」pが「偽」であるならば、「後件」qにか・か・わ・ら・ず・、命題p→qは「真」である
この結論は、一見すると、受け入れがたいように思われる。何度も質問を受けたし、私も、たくさん考えた(笑)。きっと、誰もが考えこんだのだろうし、きっと、ヴィトゲンシュタインも(笑)、考えこんだ!
話すべきことがたくさんあるので、それに、すでに、Excelなどを操作しているうちに、ちょっと飽きてきたから、次回に回す。
この表の「舞台裏」は次の如く、
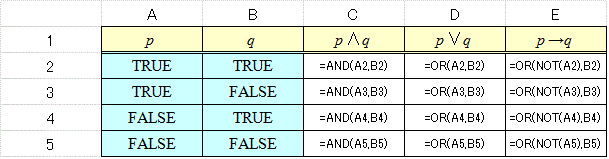
「否定」、「連言」、「選言」については、それぞれ「NOT」、「AND」、「OR」、なる「真理関数」が用意されているが、「条件法(ならば)」には、それがない。なくてもいいのは、「代用」できるからで、「代用」できることの「意味」もまた重要だから、これも次回にする。
さて、「条件法→(ならば)」の真理表についてであった。もう二年ほど前になるか?、ウィトゲンシュタイン「論理哲学論考」を読んでいた、のではなく、・・・、「ウィトゲンシュタイン『論理哲学論考』を読む」野矢茂樹(ちくま学芸文庫)を読んでいた頃だ。同じことを考えて書いてみた。今読み返してみても、なかなか良く出来ていて(笑)、あたしって、結構賢かったんじゃない?、このまま掲げておく。
トートロジーとは、その真理領域が論理空間全体にわたるような命題である。
矛盾こそが、最も多くを語る命題、なのである、続編。
「前件」が「偽」なら「後件」の「真・偽」如何に関わらず、命題は「真」となる。誤った前提からは、いかなる命題も証明さ・れ・て・し・ま・う・。いかなる命題も証明されてしまうような「世界」は、「病んだ」「世界」である。「世界」が「病んで」いるのは、誤った前提が混入したからで、ではその誤りを、発見、除去できるためには、いかなる命題も証明されてしまう、という「病み」の症候が「露見」しなければならない。だ・か・ら・、「前件」pが「偽」なら、「後件」qにおよそ何を書こうと、命題pならばqは、つ・ね・に・、「真」でな・け・れ・ば・ならない。ということのようだが、確かに、はたっ!、と膝を打たせるものがあるが、やはり、納得しやすい、とは言い難い。
「世界」を、二つの問い、pであるか?、qであるか?、で切り分けると、必ず、4つの部分ができる。
- pであり、qである。「p∧q」
- pであり、qでない。「p∧¬q」
- pでなく、qである。「¬p∧q」
- pでなく、qでない。「¬p∧¬q」
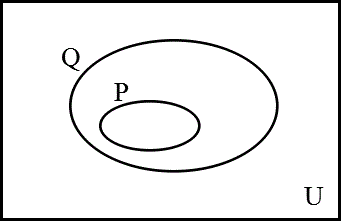
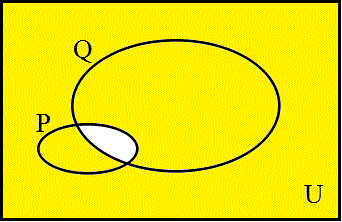
p、qの真理領域、それぞれが「真」となるような「もの」の集合、をそれぞれP、Qとすれば、下のベン(Venn)図のようなありかたが、普・通・の・「世界」である。
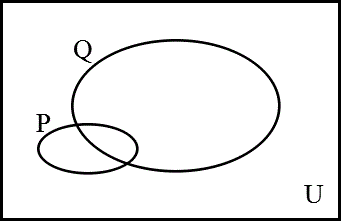
上の1〜4のどれかの領域を、空集合にしてしまうと、「包含関係」が発生する。
ところで、命題p→qが「真」である、ということは、いかなるPの要素を取り出しても、それはまたQの要素でもある、ということなのだから、pの真理領域P、が、qの真理領域Qに包含されている状態、
P⊂Q
に対応する。下の図のような按配である。これは、PをQの内側に引きずり込むことで、上の「2.pであり、qでない」の領域が、空集合になってしまったことを意味する。すなわち、
P∩¬Q=φ
これが「背理法(帰謬法)」のロジックであり、p∧¬qを「仮定」したところ、いやそんなことはあ・り・得・な・い・、という結論が得られたことで、命題p→qが「真」であることが証明されたことになるのである。
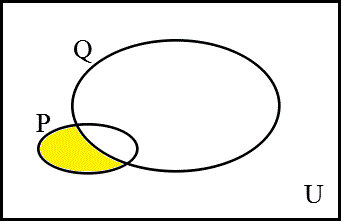
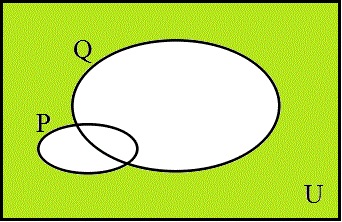
ところで、前回見たように、「条件法→(ならば)」の真理表は、「pでないか、または、q」、¬p∨qと、同一であった。対応する集合の記号で書くと、
¬P∪Q
これは、「ド・モルガンの法則」、それ自体も、間もなく「タブローの方法」での証明をご紹介できると思う、により、
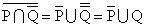
であるから、P∩¬Qの補集合である。ということは、空集合の補集合は全体集合にほかならず、p→qが「真」であるならば、
¬P∪Q=U
ということになる。つまり、¬P∪Qが「すべて」であるような「世界」では、常に、命題p→qは「真」なのである。だから、命題p→qを「真」とするような領域は、¬p∨qが「真」となる領域と、ぴったり同じだったのである。
下の左図の黄色がP∩¬Q、この領域では、命題p→qは「偽」である。ならば、この領域以外のすべての場所で、命題p→qが「真」でなければならないとすれば、・・・、きっと、そうでない「行き方」もあり得るのだろうが、その補集合、右図の緑、¬P∪Qが、命題p→qの真理領域で、な・け・れ・ば・な・ら・な・く・な・る・、のである。

前々回、論理結合子「→(ならば)」を用いた論理式、p→qが、¬p∨qで「代用」されることを見た。ならば、そこで当然生じる疑問は、論理結合子は、「¬、∧、∨、→」の4個があるというが、本当にそれだけ必要なのか?、現に「→」はなくてもすむのだから、もっと減らせないのか?、「究極的には」いくつあれば足りるのか?、という疑問が生ずる。
真理表が同じ、真、偽のパターンを示してくれれば、それらの論理結合子は、「代用」可能なのである。ほれ!、下に見るように、
- p∨qは、¬(¬p∧¬q)で、
- p∧qは、¬(¬p∨¬q)で、
「代用」できることがわかる。


こうして、論理結合子は、
- 「¬(否定)」と「∧(かつ)」、ないしは、
- 「¬(否定)」と「∨(または)」、
の二つだけで、まかなえることが分かった。さらに、実は、一つでいいのだ!、ということが知られている。「シェッファー・ストローク」と呼ばれるんだそうだが、次のような真理表を与える論理結合子を定義すると、「¬」、「∧」、「∨」のすべてが、そのそれぞれ一つだけの論理結合子の組み合わせで、「代用」できるらしい。
数学の徹底的な「形式化」を夢想したヒルベルトは、「点、直線、面の代わりに、ビール、ジョッキ、テーブルと名付けても幾何学を構成できるのだ」と言った。ドイツ人だし(笑)、大学都市の、ビアホールで、一杯やりながらの放談が、歴史に残ってしまったのだろう。ビール好きのヒルベルト氏に敬意を払って、ここでは、では、その二つの論理結合子を、それぞれ、「ビール」、「ジョッキ」と名付ける。
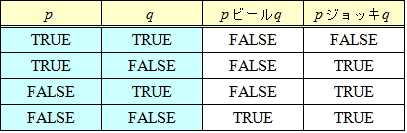
- まず、「¬p」は、「pビールp」でも「pジョッキp」でも、代用できる。

- 次に、「p∧q」は、「(pビールp)ビール(qビールq)」または、「(pジョッキq)ジョッキ(pジョッキq)」で「代用」できる。
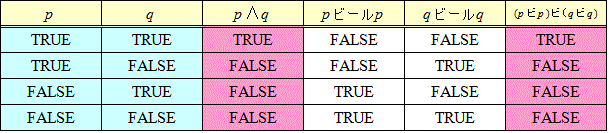
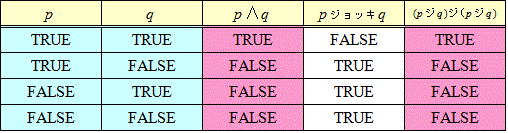
- さらに、「pまたはq」は、「(pビールq)ビール(pビールq)」または、「(pジョッキp)ジョッキ(qジョッキq)」で「代用」できる。
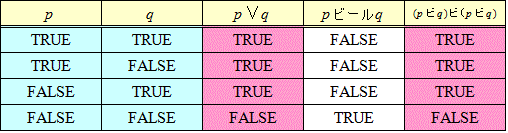
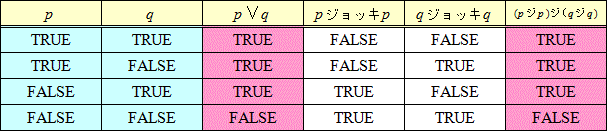
こうして「世界」が、「ビール」と「ジョッキ」で、説明できたのである。
「真理表」を用いて、「真理値分析」なるものを施し、ある命題が、「トートロジーであるか?、トートロジーでないか?」を判定する、ということをやってみよう。各々の命題変項は、「真/偽」の2値しか取りえないから、その命題がn個の命題変項を含んでいたなら、2n個の場合について検討することになり、「真理表」は、2n行の表になるであろう。
そのすべての行に対して、「真理値」が「真」となれば、その命題は、「トートロジー」である。一つでも「偽」が含まれていたら、「トートロジー」ではない。すべてが「偽」なら、「矛盾」である、ということになる。
「世界」は、「トートロジー」と「矛盾」とを両極端とし、その中間に「トートロジー」でも「矛盾」でもない、数々の命題によって、出来ている。
- 命題p→qに対して、命題¬q→¬pを、その「対偶」と呼ぶ。「対偶」は元の命題と、真偽が一致することが知られている。
つまり、(p→q)→(¬q→¬p)は、つねに正しい命題、「恒真命題」、「トートロジー」である。確かめてみよう。

一番右の欄が、全て「TRUE」となっている。これが、「トートロジー」であることの証である。
- 世に、「逆ハ必ズシモ真ナラズ」と申しまして、命題p→qに対して、命題q→pを、その「逆」と呼ぶが、これら二つの命題の真理値は、一致しない。
だから、命題(p→q)→(q→p)は、つねに正しい、とは言えない、命題である。つねに、正しくない、とも言っていない。「トートロジー」ではない、と言っているのであって、「矛盾」だとは、言っていない。

一番右の欄が、全て「TRUE」なわけでは、ない。これが、「トートロジー」でな・い・ことの証である。
- 「ド・モルガンの法則」を証明しよう。
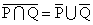
これを命題論理の言葉で書くと、
¬(p∧q)→(¬p∨¬q)

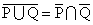
これを命題論理の言葉で書くと、
¬(p∨q)→(¬p∧¬q)

なるほど、いずれも「トートロジー」であった。「トートロジー」である、いかなる場合にも「真」である、だからこそ、それは「定理」と呼ばれるに値するのである。
改めて、「¬否定」、「∧連言」、「∨選言」、「→条件法」、の「真理表」を眺めてみる。
「世界」が、「ビール」ないしは「ジョッキ」なる、ただ一つの論理結合しで構成できることはわかったが、やはりそれは「日常言語」から余りにもかけ離れているから、分かりにくい。分かりやすくあるためには、多少の「冗長性redundancy」が必要で、だから、比較的「日常言語」に近い、これら4個の論理結合子が、選・ば・れ・た・、というわけなのだろう。
4つの論理結合子の「真理表」を下にもう一度掲げる。これを、右から左へ、逆に、「読んで」いく。○を各種論理結合子として、p○qが、「真」であることから何が言えるか?、「偽」であることから何が言えるか?
これがのちに、「タブローの方法」の作業手順の根拠になる。
- 「¬否定」の真理表

- ¬pが、「真」であるなら、か・な・ら・ず・、pは「偽」である
- ¬pが、「偽」であるなら、か・な・ら・ず・、pは「真」である
このように、ある一つの言明から、直ちに結論を下すことができるので、これを「直接帰結型」と呼び、次のような記法をとることにする。文頭の「T/F」は、それぞれ「真TRUE/偽FALSE」の略号である。
- 「∧連言」、「∨選言」、「→条件法」の真理表

- p∧qが、「真」であるなら、か・な・ら・ず・、pは「真」であり、qも「真」である・・・(i)
- p∧qが、「偽」であるなら、二・つ・の・場・合・が・あ・り・、pが「偽」であるか、qが「偽」であるかのいずれかである・・・(ii)
- p∨qが、「真」であるなら、二・つ・の・場・合・が・あ・り・、pが「真」であるか、qが「真」であるかのいずれかである・・・(iii)
- p∨qが、「偽」であるなら、か・な・ら・ず・、pは「偽」であり、qも「偽」である・・・(iv)
- p→qが、「真」であるなら、二・つ・の・場・合・が・あ・り・、pが「偽」であるか、qが「真」であるかのいずれかである・・・(v)
- p→qが、「偽」であるなら、か・な・ら・ず・、pは「真」であり、qは「偽」である・・・(vi)
(i),(iv),(vi)は「直接帰結型」であるが、(ii),(iii),(v)では、直ちに結論を下すことはできず、場合分けをしなければ、それ以上の推論を続けることがで・き・な・い・。これを「枝分かれ型」と称し、「タブローの方法」では、実際に二本の線を引いて、「枝分かれ」するのだが、HTMLでは、そんな表記は難しいので、段落を下げて二行にわたって「枝」を表示することにする。だから、反対に段落が下がっていなかったら、それは「直接帰結型」の帰結が二行にわたって書かれていることを意味する、ことにしよう。
| p∧q | p∨q | p→q |
| T |
(i)直接帰結型
T:p∧q
T:p
T:q |
(iii)枝分かれ型
T:p∨q |
(v)枝分かれ型
T:p→q |
| F |
(ii)枝分かれ型
F:p∧q |
(iv)直接帰結型
F:p∨q
F:p
F:q |
(vi)直接帰結型
F:p→q
T:p
F:q |
ではさっそく、使ってみる。前回も採用した「対偶」、これはすでに「トートロジー」であることがわかっているから、証明されるは・ず・、なのである。
(p→q)→(¬q→¬p)
- 「タブローの方法」は「背理法」のロジックを用いている。まず、一行目には、証明すべき論理式が「偽」であると、断定するのである。文頭に、F:と書く。
各文には、以後の参照のために番号、(1),(2),(3),・・・を付す。
(1) F:(p→q)→(¬q→¬p)
- この論理式は、F:A→Bの構造をとっているから、(vi)直接帰結型、で、T:A、F:Bが、直ちに言える。これを段落下げせずに、二行にわたって書く。
文末の番号は、それが帰結された根拠となった式の番号である。
(1) F:(p→q)→(¬q→¬p)
(2) T:p→q (1)
(3) F:¬q→¬p (1)
- (2)は、(v)枝分かれ型、(3)は、(vi)直接帰結型、一般に枝分かれはのちに回したほうが重複が少なくなるようなので、先に、(3)から直接帰結する事柄を、二行にわたって、段落を下げずに、書く。
(1) F:(p→q)→(¬q→¬p)
(2) T:p→q (1)
(3) F:¬q→¬p (1)
(4) T:¬q (3)
(5) F:¬p (3)
- (4),(5)いずれも直接帰結型であるから、これも先に片付けてしまう。
(1) F:(p→q)→(¬q→¬p)
(2) T:p→q (1)
(3) F:¬q→¬p (1)
(4) T:¬q (3)
(5) F:¬p (3)
(6) F:q (4)
(7) T:p (5)
- ここで(2)の枝分かれに取り掛かる。少し苦し紛れだが、こんな表記法にしよう。
(1) F:(p→q)→(¬q→¬p)
(2) T:p→q (1)
(3) F:¬q→¬p (1)
(4) T:¬q (3)
(5) F:¬p (3)
(6) F:q (4)
(7) T:p (5)
(2)
- (8) F:p (2)
- (9) T:q (2)
- ところで、よく見てみると、(7)と(8)、および、(6)と(9)、は、それぞれいずれも矛盾したことを述べている。こうして、いずれの「枝」においても、矛盾を生じて「行き止まり」となった。これは、はじめの仮定、証明すべき論理式を「偽」と仮定したことに由来する。したがって、もとの論理式は、「真」、「トートロジー」であることが証明されたことになるのだ。
矛盾を生じたことを「×」で表し、そのあとに、矛盾を生じた式番号を並べて書くことにする。
(1) F:(p→q)→(¬q→¬p)
(2) T:p→q (1)
(3) F:¬q→¬p (1)
(4) T:¬q (3)
(5) F:¬p (3)
(6) F:q (4)
(7) T:p (5)
(2)
- (8) F:p (2) ×(7),(8)
- (9) T:q (2) ×(6),(9)
「論理学入門」丹治信春(ちくま学芸文庫)の、ほんものの「タブローの方法」では、下のような図表になる。確かにずっと見やすかろう?
なお、T,Fも論理学上の特別な記号「T」と、それをひっくり返したみたいな記号を使うのだが、これまたHTMLでは「環境依存文字」になってしまう可能性がありそうなので、やめておいた次第である。

「タブローの方法」による、論理学入門、も、しばらく頓挫しているが、「現代数学入門」遠山啓(ちくま学芸文庫)で、論理学とも絡む興味深い記事を見つけた。
「代数的構造」としての、「群」、「環」、「体」に関する事柄と、関係があるようなので、そちらの定義から入る。これは、「素数入門」芹沢正三(講談社ブルーバックス)、の方が、遠山氏の文章より、わかりやすく思えたので、そこから、しかもちょっと変えて引用する。
- 群の公理
数の集合G(group)が、加法a+bについて閉じていて、
- 交換法則 a+b=b+a
- 結合法則 a+(b+c)=(a+b)+c
- 単位元 0 の存在 a+0=0+a=a
- 任意のaに対して逆元 -a の存在 a+(-a)=(-a)+a=0
を満たすとき、Gは、加法について「可換群」をなす、と称する。「可換」なのは、交換法則が成り立つからで、「群」自体の定義には、交換総則は必要とされない。
- 環の公理
数の集合R(ring)が、加法a+b、および、乗法abについて閉じていて、
- 加法の交換法則 a+b=b+a
- 加法の結合法則 a+(b+c)=(a+b)+c
- 加法の単位元 0 の存在 a+0=0+a=a
- 任意のaに対して加法の逆元 -a の存在 a+(-a)=(-a)+a=0
- 乗法の交換法則 ab=ba
- 乗法の結合法則 a(bc)=(ab)c
- 乗法の単位元 1 の存在 a・1=1・a=a
- 加法と乗法の分配法則 a(b+c)=ab+ac , a(b+c)a=bab+aca
を満たすとき、Rは、(単位元をもつ)「可換環」をなす、と称する。「可換」なのは、交換法則が成り立つからであろう。こう言っている以上、「単位元をもたない」「環」も存在するのだろう。
- 体の公理
数の集合K(ドイツ語のKorper、oの上には「・・」、ウムラウトが乗っているが、これも「環境依存文字」になりそうだから、省略、英語だとcorpusまたはfield)が、加法a+b、および、乗法abについて閉じていて、
上の「環の公理」i〜vii、および、ixに加え、
- 任意の0でないaに対して乗法の逆元 a-1 の存在 a・a-1=a-1・a=1
を満たすとき、Kは「体」をなす、と称する。
「体」は、加法、そして、加法の逆元がある以上、減法、そして乗法、さらに、乗法の逆元がある以上、非除数が0でないものに対しては、除法もできる、システムである、ということらしい。
加法の単位元0と、乗法の単位元1だけは、絶対に含んでないといけないから、集合{0,1}は、最小の「体」をなす。この集合の中で、「加法」と「乗法」の演算を定義する。
アナロジーとしては、
- これは2進法の下1桁を表している、
0+0=0 , 0+1=1 , 1+0=1 , 1+1=10
0・0=0 , 0・1=0 , 1・0=0 , 1・1=1
- あるいは、(mod 2)の「剰余類」を表している、0を「偶数」、1を「奇数」になぞらえると、
偶数+偶数=偶数 , 偶数+奇数=奇数 , 奇数+偶数=奇数 , 奇数+奇数=偶数
偶数・偶数=偶数 , 偶数・奇数=偶数 , 奇数・偶数=偶数 , 奇数・奇数=奇数
先日「広辞苑」を引いて、サイコロ賭博の「丁/半」がそれぞれ「偶数even_number/奇数odd_number」、evenは「平、平等」、oddは「半端」であって、「丁」の語源は、課税対象となる成年男子、であることも学んだから、それになぞらえてもよい。奇をてらってやってみると、0が「丁」、1が「半」であるから、
丁+丁=丁 , 丁+半=半 , 半+丁=半 , 半+半=丁
丁・丁=丁 , 丁・半=丁 , 半・丁=丁 , 半・半=半
いずれにしても、「0/1」の二値で、「答」が出るこのシステムは、「真TRUE/偽FALSE」の「答」が出る命題論理の世界と、対応付けられそうではないか?
この「体」{0,1}における「加法」と「乗法」の演算規則を、表にすると、
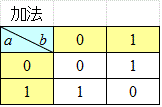
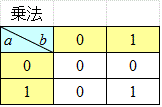
Excel関数式の「舞台裏」は、こんな感じ、


命題論理の「世界」は、もちろん「ビール」または「ジョッキ」のただ一つでもよかったのだが、「¬、∧、∨、→」の4つの論理結合子ですべてが「語られる」世界であった。
ならば、それらの「真理表」と同じになる「演算結果」をこの「体」{0,1}内の二つの演算「加法」と「乗法」で、表現できれば、命題論理の「世界」と、この体{0,1}、とが、同じ「構造」をもっている、と断言してかまわないのだろう?、嗚呼、三十数年たって、やっと、わかった!、「構造主義」って、こんなことから始まったのだね?
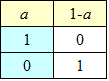
- まず、否定「¬」、「TRUE/FALSE」をそれぞれ「1/0」に対応付けると、なるほど、「¬」は、演算「1-a」に、対応することが、わかった。


- 次に、かつ「∧」、
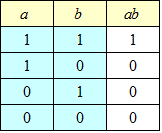
これは、そのまま乗法、「∧」は、演算「ab」に対応付けられる。
- または「∨」は、「¬」と「∧」を用いて書き換えることができた。ド・モルガンの法則により、
¬(A∨B)=¬A∧¬B
A∨B=¬{¬(A∨B)}=¬(¬A∧¬B)
これを、上ですでに得られた、対応関係に従って、「翻訳」すると、
- ¬A・・・1-a
- ¬B・・・1-b
- ¬A∧¬B・・・(1-a)(1-b)
- ¬(¬A∧¬B)・・・1-(1-a)(1-b)=a+b-ab
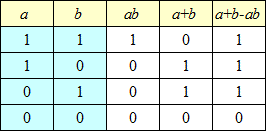
「∨」は、演算「a+b-ab」に対応付けられる。
上の表で、1行目は、a+b-ab=0-1=-1ではないか?、であるが、この{0,1}の「世界」では、1+1=0だから、1=0-1=-1、なのである。
- 最後に、ならば「→」。A→Bは、¬A∨Bと、「真理値」が同じであることは、前に話した。ならば、これも「翻訳」すればよかろう。
- A・・・a
- ¬B・・・1-b
- ¬A∨B=¬(A∧¬B)・・・1-a(1-b)=1-a+ab

うわぁ!、こうして、「世界」は、(mod 2)の「剰余類」で、できていることが、わかったのである。