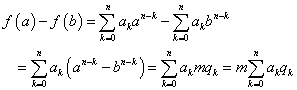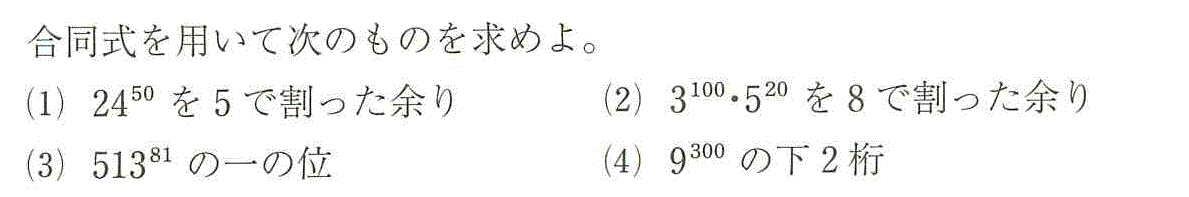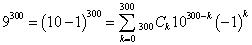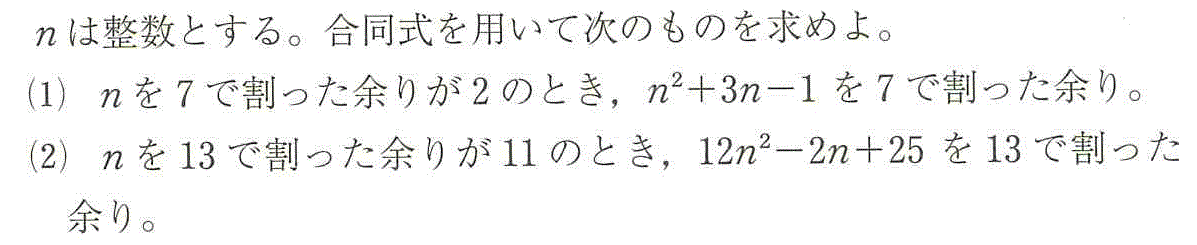「合同式congruence_equation」の研究
- [定義]
整数a,b,mに対して、
a-bがmの整数倍のとき、
aはmを法modulusとしてbと合同である、といい、
a≡b (mod m)と書く。
- [定理1]a≡b (mod m)となるための必要十分条件は、a,bをmで割った余りが等しいことである。
[証明]
- a≡b (mod m)→a,bをmで割った余りが等しいを示す。
a,bをmで割った余りをそれぞれr1,r2とおくと、
a=ma'+r1ただし、0≦r1<m
xb=mb'+r2ただし、0≦r2<m
a-b=m(a'-b')+(r1-r2)・・・(1)
ここで、
0≦r1<m
-m<-r2≦0
であるから、
-m<r1-r2<m・・・(2)
一方、a≡bであるから、a-bは、mの整数倍であり、
(1)式より、r1-r2もmの整数倍でなければならない。
(2)の範囲の中でこれを満たすのは、r1-r2=0のみである。
よって、r1=r2
- a,bをmで割った余りが等しい→a≡b (mod m)を示す。
a,bをmで割った余りがいずれもrとすると、
a=ma'+r
b=mb'+r
ただし、0≦r<m
a-b=m(a'-b')
a-bはmの整数倍である。
- [定理2]mを法とするとき、次の3式(同値律)がなりたつ。
- 反射律 a≡a (mod m)
- 対称律 a≡b (mod m)ならばb≡a (mod m)
- 推移律 a≡b (mod m),b≡c (mod m)ならばa≡c (mod m)
[証明]
- a=ma'+rただし、0≦r<m、とすると、
a-a=0すなわち、a≡a
- a≡b (mod m)から、
a=ma'+r,b=mb'+rただし、0≦r<m
b-a=m(b'-a')よって、b≡a
- a≡b (mod m)から、
a=ma'+r,b=mb'+rただし、0≦r<m
b≡c (mod m)から、
b=mb'+r,c=mc'+rただし、0≦r<m
a-c=m(a'-c')よって、a≡c
- [定理3]a≡b (mod m),c≡d (mod m)のとき、次の各式が成立する。
- a+c≡b+d (mod m)
- a-c≡b-d (mod m)
- ac≡bd (mod m)
- an≡bn (mod m)ただしnは自然数
[証明]
a≡b (mod m)より、a-b=mq1
c≡d (mod m)より、c-d=mq2
- (a+c)-(b+d)=(a-b)+(c-d)=m(q1+q2)
- (a-c)-(b-d)=(a-b)-(c-d)=m(q1-q2)
- ac-bd=(b+mq1)(d+mq2)-bd
=bmq2+dmq1+m2q1q2
=m(bq2+dq1+mq1q2)
- 数学的帰納法による。
- n=1のときa≡b (mod m)・・・(ア)
- n=kに対して、an≡bk (mod m)と仮定。
iiiより、aak≡bbk (mod m)
すなわち、ak+1≡bk+1 (mod m)・・・(イ)
(ア)(イ)より、任意の自然数nに対して、an≡bn (mod m)
- [定理3・系1]
a≡b (mod m)のとき、任意の整数nに対して、
a≡b+mn (mod m)
[証明]
a≡b (mod m)より、a-b=mq
a-(b+mn)=mq-mn=m(q-n)
- [定理3・系2]
整数係数の整式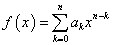 に対して、
に対して、
a≡b (mod m)のとき、f(a)≡f(b) (mod m)
[証明]
a≡b (mod m)だから、k=0,1,2,・・・,n-1に対して、[定理3iv]より、
an-k≡bn-k (mod m)
また、a0≡b0 (mod m)
よって、k=0,1,2,・・・,nに対して、an-k≡bn-k (mod m)
an-k≡bn-k=mqkと書くことができる。
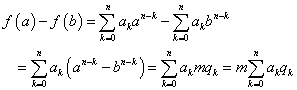
- [定理4]ac≡bc (mod m)のとき、(c,m)=gならば、
a≡b (mod m/g)
ここに、(c,m)=gとは、c,mの最大公約数がgであることをあらわす。
[証明](c,m)=gより、c=gc',m=gm'とおくことができる。
ここに、(c',m')=1すなわち、c',m'は互いに素である。
ac≡bc (mod m)より、ac-bc=mq=gm'q
一方、ac-bc=c(a-b)=gc'(a-b)
すなわち、gm'q=gc'(a-b)
すなわち、m'q=c'(a-b)
(c',m')=1だから、a-bはm'で割り切れる。すなわち、a-bはm/gで割り切れる。
- [定理4・系]ac≡bc (mod m)のとき、(c,m)=1ならば、
a≡b (mod m)
- [定理3i〜iii]では、「加・減・乗」の3つの演算に関しては、「合同式」が通常の数式の等式と同様に扱えることが明らかになった。
しかし、「除」に関しては、[定理4・系]が示すように、序数と法が互いに素であるときに限り、行うことができる。
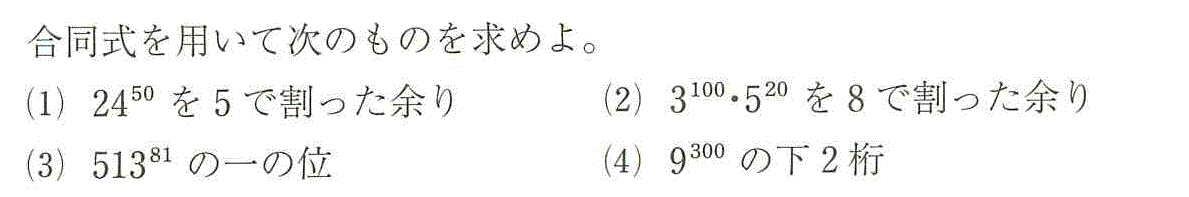
- (1)24≡4 (mod 5)、[定理3iv]より、2450≡450 (mod 5)
450=1625、16≡1 (mod 5)、同様に、1625≡125 (mod 5)
よって、2450≡1 (mod 5)
- (2)3100520=9502510
9≡1 (mod 8)、25≡1 (mod 8)だから、
[定理3iv]より、950≡1 (mod 8)、2510≡1 (mod 8)
[定理3iii]より、9502510≡1 (mod 8)
すなわち、3100520≡1 (mod 8)
- (3)51381を10で割った余りを求めればよい。
513≡3 (mod 10)、[定理3iv]より、51381≡381 (mod 10)
381=34×20+1=8120×3
81≡1 (mod 10)、[定理3iv]より、8120≡1 (mod 10)
[定理3iii]より、8120×3≡1×3 (mod 10)
よって、51381≡3 (mod 10)
- (4)9300を100で割った余りを求めればよい。
二項定理より、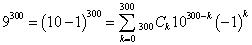
右辺のk=0からk=298に対応する項はすべて100で割り切れるから、
9300≡300C299101(-1)299+300C300100(-1)300≡300・10・(-1)+1≡1 (mod 100)
よって、9300≡1 (mod 100)
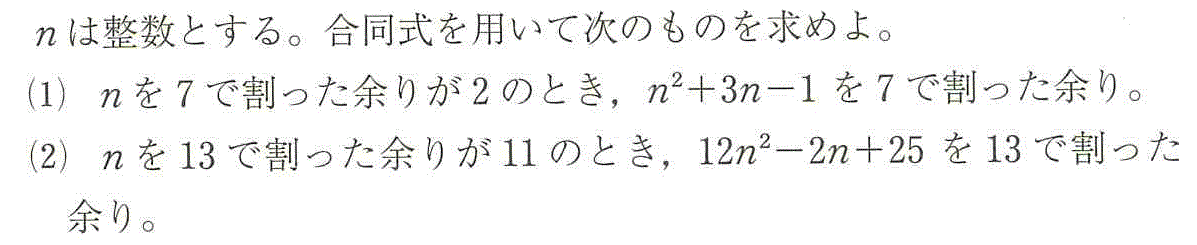
- (1)n≡2 (mod 7)だから、
[定理3iv]より、n2≡22≡4 (mod 7)
[定理3iii]より、3n≡3・2≡6 (mod 7)
[定理3i,ii]より、n2+3n-1≡4+6-1≡9≡2 (mod 7)
- (2)n≡11 (mod 13)だから、
[定理3iv、系1]より、n2≡112≡121≡13×9+4≡4 (mod 13)
[定理3iii、系1]より、12n2≡12×4≡48≡13×3+9≡9 (mod 13)
[定理3iii、系1]より、2n≡2×11≡22≡13×1+9≡9 (mod 13)
[定理3i,ii、系1]より、12n2-2n+25≡9-9+25≡25≡13×1+12≡12 (mod 13)
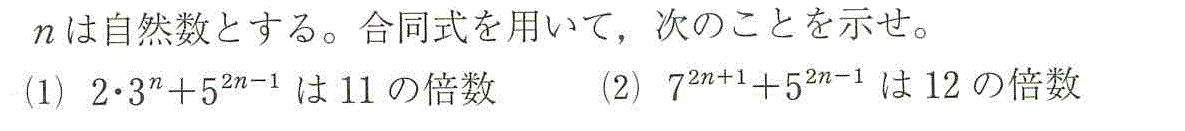
- (1)2・3n+52n-1≡0 (mod 11)を示したい。
52n-1=52(n-1)+1=5・25n-1
25≡3 (mod 11)、[定理3iii,iv]より、5・25n-1≡5・3n-1 (mod 11)
[定理3i]より、
2・3n+5・25n-1≡2・3n+5・3n-1≡6・3n-1+5・3n-1≡11・3n-1≡0 (mod 11)
よって、2・3n+52n-1≡0 (mod 11)
- (2)72n+1+52n-1≡0 (mod 12)を示したい。
72n+1+52n-1=72n+1+52(n-1)+1=7・(72)n+5・(52)n-1=7・49n+5・25n-1
[定理3・系1]より、49≡12×4+1≡1 (mod 12)、25≡12×2+1≡1 (mod 12)
[定理3iv,iii,i]より、7・49n+5・25n-1≡7・1n+5・1n-1≡7+5≡12≡0 (mod 12)
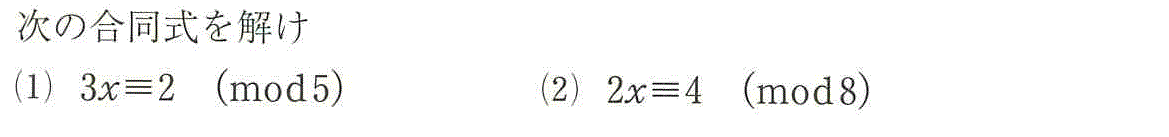
- (1)3を何倍かして、5で割ると1余る数にしたい。
3x≡2 (mod 5)
[定理3iii]より、6x≡4 (mod 5)
[定理3・系1]より、5x+x≡x≡4 (mod 5)
- (2)3を何倍しても、8で割ると1余る数にはできない。
これは、[定理4]の適用場面で、
2x≡4 (mod 8)
(2,8)=2だから、つまり、2と8の最大公約数は2だから、
x≡2 (mod 4)
「合同式を解く」とは、未知数xの与えられた法に対する剰余を求めることだから、
x≡□ (mod 8)でなければならない。
x≡2 (mod 4)から、x-2=4qすなわち、x=4q+2
4で割ると2余る数を、8で割った余りは?、これは、qが2の倍数であるか否かで異なる。
- q=2q'のとき・・・x=8q'+2すなわち、x≡2 (mod 8)
- q=2q'+1のとき・・・x=8q'+6すなわち、x≡6 (mod 8)
よって、x≡2,6 (mod 8)
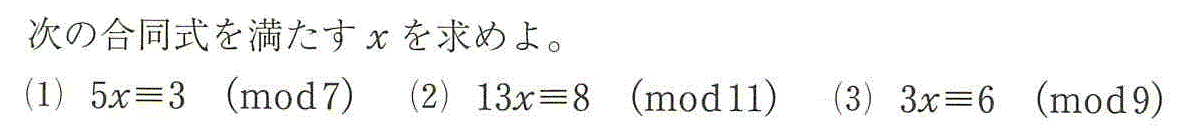
- (1)5を何倍かして、7で割ると1余る数にしたい。
5x≡3 (mod 7)
[定理3iii]より、15x≡9≡2 (mod 7)
[定理3・系1]より、2×7x+x≡x≡2 (mod 7)
- (2)13を何倍かして、11で割ると1余る数にしたい。78=13×6=11×7+1
13x≡8 (mod 11)
[定理3iii]より、78x≡48≡4 (mod 11)
[定理3・系1]より、7×11x+x≡x≡4 (mod 11)
- (3)3x≡6 (mod 9)
(3,9)=3であるから、[定理4]より、x≡2 (mod 3)
すなわち、x=3q+2
qを3の剰余類に分類する。
- q=3q'のとき、・・・x=9q'+2
- q=3q'+1のとき、・・・x=9q'+5
- q=3q'+2のとき、・・・x=9q'+8
よって、x≡2,5,8 (mod 9)
ところで、「解のない」合同式(合同方程式)が存在する。
[定理5]合同式ax≡b (mod m)は、(a,m)がbを割り切るとき、そのときだけ解をもつ。
[例]2x≡5 (mod 4)は、解をもたない。
2x-5=4q
左辺は奇数であり、右辺は偶数であるから、このような整数x,qは存在しない。
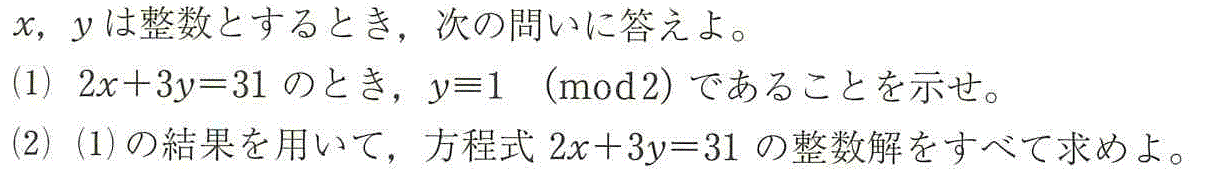
- (1)x,yの係数を比較すると、2より3の方が大きいから、3=2×1+1として、
2x+3y≡2x+(2×1+1)y≡y (mod 2)
一方、31≡1 (mod 2)
よって、y≡1 (mod 2)
- (2)y=2k+1 (kは整数)とすると、
2x+3y=31
2x+3(2k+1)=31
2x+6k=28
x+3k=14
x=-3k+14
よって、整数kに対して、(x,y)=(-3k+14,2k+1)

- (1)11x+13y=23
11x+13y≡11x+(11+2)y≡2y (mod 11)
23≡2×11+1≡1 (mod 11)
よって、2y≡1 (mod 11)
12y≡11y+y≡y≡6 (mod 11)
y=11k+6 (kは整数)とすると、
11x+13(11k+6)=23
11x+13×11k=23-78=-55
x+13k=-5
よって、整数kに対して、(x,y)=(-13k-5,11k+6)
- (2)39x-29y=326
39x-29y≡(29+10)x-29y≡10x (mod 29)
326≡29×11+7≡7 (mod 29)
よって、10x≡7 (mod 29)
30x≡29x+x≡x≡21 (mod 29)
x=29k+21 (kは整数)とすると、
39(29k+21)-29y=326
39×29k-29y=326-39×21=326-819=493=-29×17
39k-y=-17
よって、整数kに対して、(x,y)=(29k+21,39k+17)
自然数a,bがあり、
(a,b)=1、すなわち、a,bは互いに素であるとする。
このとき、方程式、
ax+by=1
を満たす、0でない整数解(x,y)が無数に存在する。
その中で、0<|x|<b,0<y<aとなるものと、
0<x<b,0<|y|<aとなるものとが、各一組ずつ存在する。
[証明]
- (a,b)=1であるから、a,bの最小公倍数l=abである。
すなわち、lはaで割り切れ、かつ、
n=1,2,3,・・・,a-1のすべてのnに対して、
nbはaで割り切れない。
そこで、
nb=qa+rただし、qは自然数、0<r0<a
となるq,rが存在する。
- 異なるnに対しては、rも異なることを示す。背理法による。
n≠n'に対して、
nb=qa+r
n'b=q'a+r
なる、自然数q,q'が存在すると仮定する。
(n-n')b=(q-q')aとなる。
- n>n'とすると、q>q'で、n'<n<aだから、0<n-n'<a
これは、a,bの最小公倍数がl=abであるのに、
aよりはるかに小さいn-n'に対して、(n-n')bがすでにaの倍数であると主張しており、明らかに不合理である。
- n<n'の場合も同様である。
よって、異なるnに対しては、rも異なることが示された。そこで、
nb=q(n)a+r(n) ただし、n=1,2,3,・・・,a-1
と書くことができる。
- ところで、r(n)は、nbをaで割った余りなのだから、1,2,3,・・・,a-1のいずれかに等しい。
nごとに異なるa-1個のr(n)が、同じくa-1個の1,2,3,・・・,a-1という値のいずれかをとるのであるから、これは一対一の対応である。
したがって、a-1個のr(n)のうちに、かならず一つだけ、1に等しいものがある。
それをr(a')、ただし、0<a'<a、としよう。
すなわち、a'b=qa+1と書ける。
すなわち、-qa+a'b=1
であるから、(x,y)=(-q,a')は、与えられた方程式の一つの解である。
ここに、qa<a'b<abであるから、0<q<b
また、0<a'<aであるから、この解は、
0<|x|<b,0<y<aの条件を満たしている。
0<q<bしたがって、0<b-q<b
q'=b-qとおくと、0<q'<b
(q'-b)a+a'b=1
q'a-(a-a')b=1
a''=a-a'とおくと、0<a''<a
q'a-a''b=1
したがって、(x,y)=(q',-a'')も、与えられた方程式の一つの解である。
0<q'<b,0<a''<aであるから、この解は、
0<x<b,0<|y|<aの条件を満たしている。
- 2x+3y=31・・・(ア)
(2,3)=1であるから、2x'+3y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(31x',31y')である。
2x'+3y'=1を解く。・・・(イ)
x',y'の係数2,3を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(2,3)=1、すなわち、2と3は互いに素であるから、かならずこれは可能である。
2x'+(2×1+1)y'=1
2(x'+y')+y'=1
こうして、第2項の係数が1となった。
明らかに、x'+y'=0,y=1は、解である。
この連立方程式を解くと、
(x',y')=(-1,1)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が絶対値において3より小さい正数であり、かつ、y'が2より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
2x'+3y'=1・・・(イ)
2(-1)+3・1=1・・・(ウ)
2(x'+1)+3(y'-1)=0・・・(イ)-(ウ)
すなわち、
2(x'+1)=-3(y'-1)
ここに、(2,3)=1であるから、
x'+1=-3k
y'-1=2k
すなわち、
(x',y')=(-3k-1,2k+1)
無論、k=0のときが、上の、
x'が絶対値において3より小さい正数であり、かつ、y'が2より小さい正数である特殊解、
(x',y')=(-1,1)
である。
では、
x'が3より小さい正数であり、かつ、y'が絶対値において2より小さい正数である特殊解、
の方はどうか?
k=-1とすればよい。すなわち、
(x',y')=(2,-1)
(ア)に戻ると、解は次のように書ける。
(x,y)=(31(-3k-1),31(2k+1))
もう少しシンプルな表現にしたい。k'=31kとおくと、
(x,y)=(-3k'-31,2k'+31)
さらに、たとえば、k''=k'+15とおくと、
(x,y)=(-3(k''-15)-31,2(k''-15)+31)=(-3k''+14,2k''+1)
または、たとえば、k'''=k'+10とおくと、
(x,y)=(-3(k'''-10)-31,2(k'''-10)+31)=(-3k'''-1,2k'''+11)
ここでも、端数の絶対値を31より小さくする方法が、ただ2通り、存在するのである。
-
- (1)11x+13y=23・・・(ア)
(11,13)=1であるから、11x'+13y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(23x',23y')である。
11x'+13y'=1を解く。・・・(イ)
x',y'の係数11,13を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(11,13)=1、すなわち、11と13は互いに素であるから、かならずこれは可能である。
11x'+(11×1+2)y'=1
11(x'+y')+2y'=1
(2×5+1)(x'+y')+2y'=1
2{5(x'+y')+y'}+(x'+y')=1
2(5x'+6y')+(x'+y')=1
こうして、第2項の係数が1となった。
明らかに、5x'+6y'=0,x'+y=1は、解である。
この連立方程式を解くと、
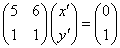
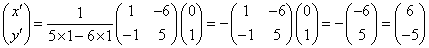
(x',y')=(6,-5)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が13より小さい正数であり、かつ、y'が絶対値において11より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
11x'+13y'=1・・・(イ)
11・6+13(-5)=1・・・(ウ)
11(x'-6)+13(y'+5)=0・・・(イ)-(ウ)
すなわち、
11(x'-6)=-13(y'+5)
ここに、(11,13)=1であるから、
x'-6=-13k
y'+5=11k
すなわち、
(x',y')=(-13k+6,11k-5)
無論、k=0のときが、上の、
x'が13より小さい正数であり、かつ、y'が絶対値において11より小さい正数である特殊解、
(x',y')=(6,-5)
である。
では、
x'が絶対値において13より小さい正数であり、かつ、y'が11より小さい正数である特殊解、
の方はどうか?
k=1とすればよい。すなわち、
(x',y')=(-7,6)
(ア)に戻ると、解は次のように書ける。
(x,y)=(23(-13k+6),23(11k-5))
もう少しシンプルな表現にしたい。k'=23kとおくと、
(x,y)=(-13k'+23×6,11k'-23×5)
23×6=13×10+8,23×5=11×10+5であるから、
さらに、たとえば、k''=k'-10とおくと、
(x,y)=(-13(k''+10)+13×10+8,11(k''+10)-11×10-5)=(-13k''+8,11k''-5)
23×6=13×11-5,23×5=11×11-6であるから、
または、たとえば、k'''=k'-11とおくと、
(x,y)=(-3(k'''+11)+13×11-5,11(k'''+11)-11×11+6)=(-13k'''-5,11k'''+6)
ここでも、端数の絶対値を23より小さくする方法が、ただ2通り、存在するのである。
- (2)39x-29y=326・・・(ア)
(39,29)=1であるから、39x'-29y'=1は整数解をもつ。
得られた(x',y')に対して、(x,y)=(326x',326y')である。
39x'-29y'=1を解く。・・・(イ)
x',y'の係数の絶対値39,29を「ユークリッド互助法」により、次第に小さくし、最終的にはどちらかを1に帰着させる。
(39,29)=1、すなわち、39と29は互いに素であるから、かならずこれは可能である。
(29×1+10)x'-29y'=1
29(x'-y')+10x'=1
(10×2+9)(x'-y')+10x'=1
10{2(x'-y')+x'}+9(x'-y')=1
10(3x'-2y')+9(x'-y')=1
(9×1+1)(3x'-2y')+9(x'-y')=1
9{(3x'-2y')+(x'-y')}+(3x'-2y')=1
9(4x'-3y')+(3x'-2y')=1
こうして、第2項の係数が1となった。
明らかに、4x'-3y'=0,3x'-2y=1は、解である。
この連立方程式を解くと、
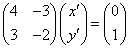
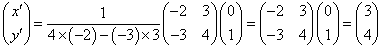
(x',y')=(3,4)
これは(イ)の無数に存在する整数解のうちのひとつの解(特殊解)である。
ちなみにこれは、x'が29より小さい正数であり、かつ、-y'が絶対値において39より小さい正数である特殊解である。
(イ)に代入して、辺々引くと、
39x'-29y'=1・・・(イ)
39・3-29・4=1・・・(ウ)
39(x'-3)-29(y'-4)=0・・・(イ)-(ウ)
すなわち、
39(x'-3)=29(y'-4)
ここに、(39,29)=1であるから、
x'-3=29k
y'-4=39k
すなわち、
(x',y')=(29k+3,39k+4)
無論、k=0のときが、上の、
x'が29より小さい正数であり、かつ、-y'が絶対値において39より小さい正数である特殊解、
(x',y')=(3,4)
である。
では、
x'が絶対値において29より小さい正数であり、かつ、-y'が39より小さい正数である特殊解、
の方はどうか?
k=-1とすればよい。すなわち、
(x',y')=(-26,-35)
(ア)に戻ると、解は次のように書ける。
(x,y)=(326(29k+3),326(39k+4))
もう少しシンプルな表現にしたい。k'=326kとおくと、
(x,y)=(29k'+326×3,39k'+326×4)
326×3=29×33+21,326×4=39×33+17であるから、
さらに、たとえば、k''=k'+33とおくと、
(x,y)=(29(k''-33)+29×33+21,39(k''-33)+39×33+17)=(29k''+21,39k''+17)
326×3=29×34-8,326×4=39×34-22であるから、
または、たとえば、k'''=k'+34とおくと、
(x,y)=(29(k''-34)+29×34-8,39(k''-34)+39×34-22)=(29k''-8,39k''-22)
ここでも、端数の絶対値を326より小さくする方法が、ただ2通り、存在するのである。
「新課程」初年度のこの学年の教科書を、私は見ていないから、たとえば新たに盛り込まれた「2元1次不定方程式の整数解」問題、いわゆる「ディオファントス方程式」でございますな、・・・、の解法を、高校生にどう説明すべきか?、を知らなかった。単なる「趣味」として、高木貞治「新式算術入門」(ちくま学芸文庫)を読んで、まだ「路頭に迷う」とは予想していなかった(笑)昨年の秋ごろ、没頭していたから、「得意」分野ではあるのだが、高木貞治が紹介している「オイラーの方法」、しかも高木貞治が、「あとは、わかるでしょ?」みたいに(笑)放り出している部分は、自己流で補って、編み出した方法は、以前ご紹介したように、こんな感じ(↓)で、
「冷笑に満ちた『修辞疑問文』のさなかで?」
こんなに延々と数式を羅列したのでは、ほとんどが文科系志望の生徒さんたちは、辟易してしまうだろう、とも思えた。案の定、「先生、教科書に書いてあるの、もっと簡単そうだよ」、と、声がかかった。斜に構えて、にやにや「冷笑」しているだけではなく(笑)、ちゃんと指摘してくれる、「進学校」ではない生徒さんの朴訥さが、ありがたい(笑)。
やっていることの「本質」は(笑)、同じ、「ユークリッド互除法」なのだが、確かに、わかりやすい説明にはなっている。こうして初めて知った(笑)教科書風の、ディオファントス解法を、紹介する。以前のと同じ例題を用いよう。
39x-29y=326
ここで、39と29はたがいに素であるから、
39x'-29y'=1
は整数解をもつ。高木貞治のきわめてエレガントなその証明も、以前ご紹介(↓)したが、
「人が饒舌だとしたら、それは、何かそれ以外のことを、決して喋りたく『ない』からだ。」
高校教科書では、ここは証明なしで断言しているのだと思う。
得られた一組の(x',y')に対して、(x,y)=(326x',326y')とあらわされることは明らかである。
「ユークリッド互除法」を39,29に適用する。たがいに素であることは明白だから、「1」に至るまで続く筈である。
39=29×1+10・・・(1)
29=10×2+9・・・(2)
10=9×1+1・・・(3)
これで「収束」した。この3式を組み立てなおして、目標である、
1=39x'-29y'
を「再構成」しよう、と言うのである。各式の第1項を移項して、左辺右辺を入れ替え、かつ、番号を逆順にして並べて見ると、
1=10-9×1・・・(3')
9=29-10×2・・・(2')
10=39-29×1・・・(1')
(3')式の「9」に(2')式を「代入」する。
1=10-(29-10×2)×1
「10」を同類項としてまとめると、29と10、もちろんたがいに素、の「1次結合」になる。もちろん教科書はそんな小難しいことは言わない(笑)。
1=10×(1+2)-29×1
1=10×3-29×1
「10」に(1')を「代入」し、おなじく「29」を同類項としてまとめると、今度こそ、39と29の「1次結合」になり、これが求めるものなのであった!
1=(39-29×1)×3-29×1
1=39×3-29×(3+1)
1=39×3-29×4
ほら!(笑)こうして、(x',y')=(3,4)が得られた、したがって、(x,y)=(326×3,326×4)が解である。
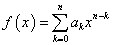 に対して、
に対して、