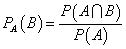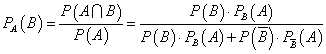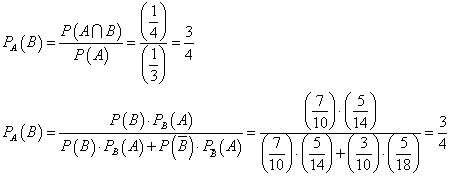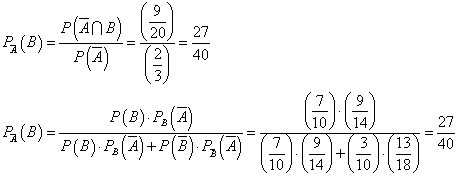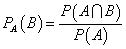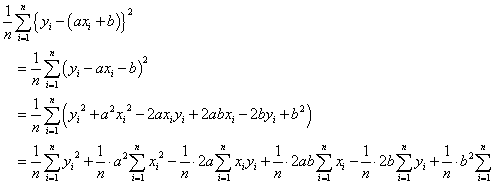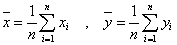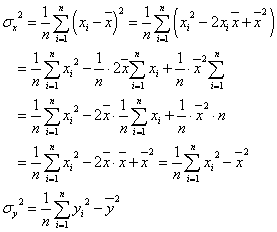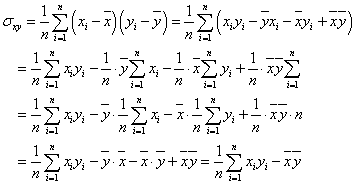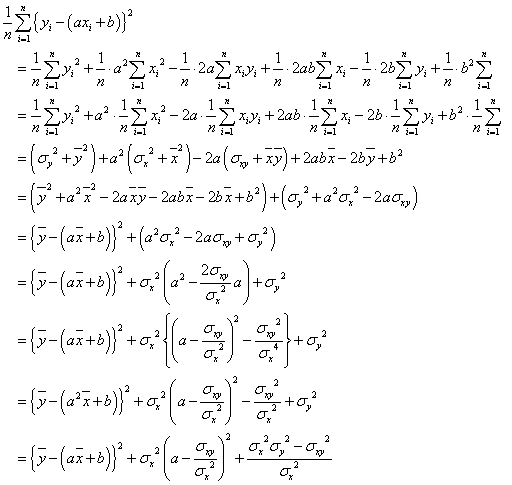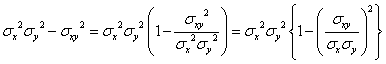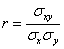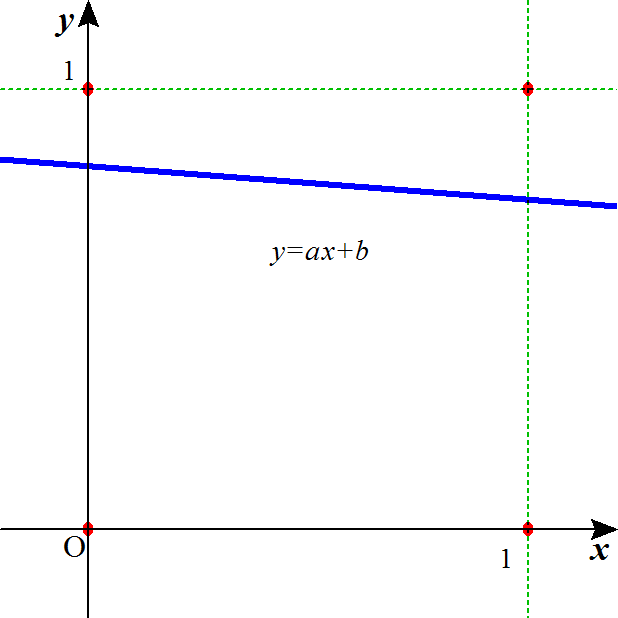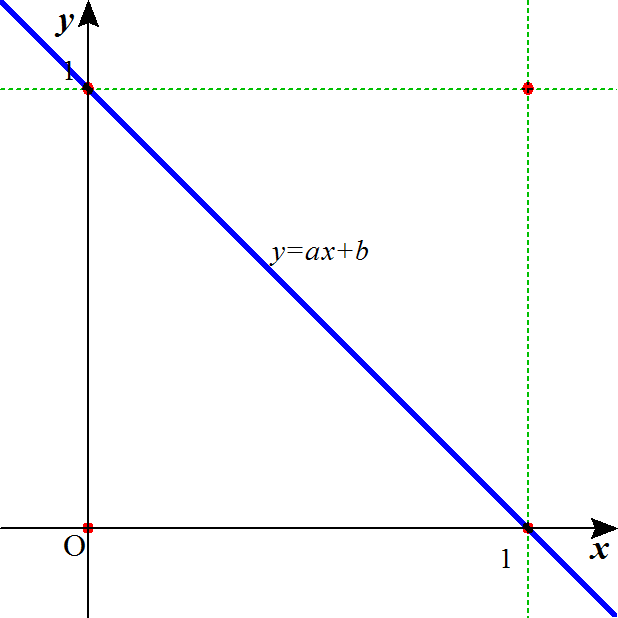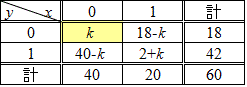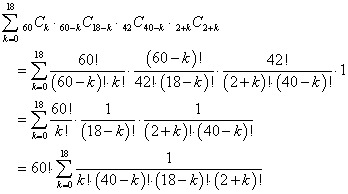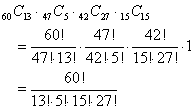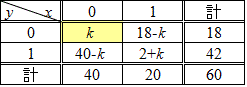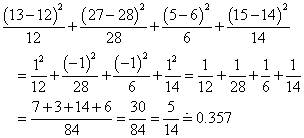二つの問い、「あなたは、Aであるか?」、「あなたは、Bであるか?」、によって、世界は4つの部分に切り分けられる。
- Aであり、Bである。A∩B
- Aであり、Bでない。A∩¬B
- Aでなく、Bである。¬A∩B
- Aでなく、Bでない。¬A∩¬B
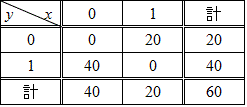
次のような「調査結果」があったとしよう。全体集合Uとして、n(U)=60、60の「標本(サンプル)」に聞き取り調査をしたのである。
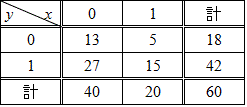
- x=1、Aである、例えば、「政権党を支持している」
- x=0、Aでない、例えば、「政権党を支持しているわけではない」
- y=1、Bである、例えば、「投票に行く」
- y=0、Bでない、例えば、「投票に行くわけではない」
という調査であるならば、この調査結果から、
「政権党支持者のなかで、投票に行く人の割合」が15/20=0.75であるのに対して、
「政権党支持者ではない人のなかで、投票に行く人の割合」が27/40<0.75であることから、
「投票結果は、実・際・の・、政権党支持率を、多めに、見積もっている」という結論を下すことができる、ことになる。投票した人の中での政権党支持率は、15/42=5/14≒0.36であるところ、投票した人も、投票しない人も含めた「潜在的な」政権党支持率は、20/60=0.333だからである。
もちろん、政権党支持者が投票所で間違いなく政権党に投票し、政権党支持者でない者が間違いなく、政権党に投票しない、ことを前提として、である。論理的に正確であるためには、夥しい「但し書き」が必要になるのはやむを得ない。
- x=1、Aである、例えば、「薬○○を服用した」
- x=0、Aでない、例えば、「薬○○を服用したわけではない」
- y=1、Bである、例えば、「病△△が治癒した」
- y=0、Bでない、例えば、「病△△が治癒したわけではない」
という調査であるならば、この調査結果から、
「薬○○を服用した人のなかで、病△△が治癒した人の割合」が15/20=0.75であるのに対して、
「薬○○を服用したわけではない人のなかで、病△△が治癒した人の割合」が27/40<0.75であることから、
「薬○○を服用することで、病△△の治癒の可能性が高まる、つまり、薬○○には薬効がある」という結論を下すことができる、ことになる。
次のような「変奏」も可能である。
- x=1、Aである、例えば、「女である」
- x=0、Aでない、例えば、「女であるわけではない」
- y=1、Bである、例えば、「喫煙者でない」
- y=0、Bでない、例えば、「喫煙者でないわけではない」
という調査であるならば、この調査結果から、
「女である人のなかで、喫煙者でない人の割合」が15/20=0.75であるのに対して、
「女であるわけではない人のなかで、喫煙者でない人の割合」が27/40<0.75であることから、
「女の人の方が、喫煙者でない可能性が高い」という結論を下すことができる、ことになる。
ああ、だったら、男の方が、タバコを吸うやつが多い、ってことね!、と言っては、いけない、言葉を「正しく」用いなければならない、「論理学」を学ぶ「意味」があるとすれば、この一点に尽きるわけで、上の二例に比べて、三番目の例が、どう違うのか?
あなたが男であるか?、あなたが女であるか?、は、既にして「二つの問い」なのである。
- Aであり、Bである。A∩B・・・男であり、女である
- Aであり、Bでない。A∩¬B・・・男であり、女でない
- Aでなく、Bである。¬A∩B・・・男でなく、女である
- Aでなく、Bでない。¬A∩¬B・・・男でなく、女でない
A∩B・・・男であり、女である、¬A∩¬B・・・男でなく、女でない、なる集合が、どんなに小さくても、それが存在する限り、無視することは暴力的なのである。
あなたは男ではない?、では、女なのですね。
あなたは女ではない?、では、男なのですね。
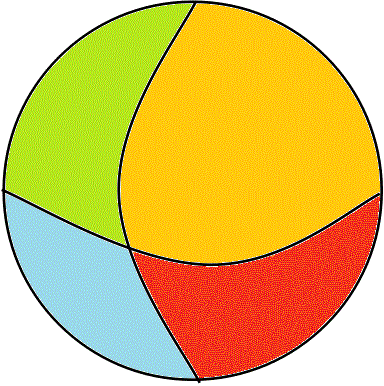
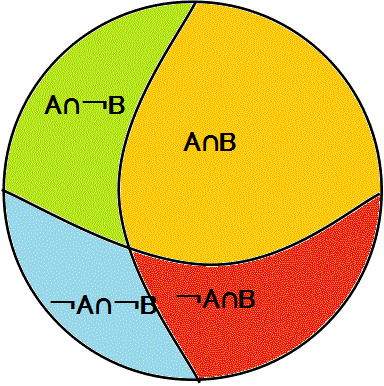
そうではなくて、繰り返すが、「世界」は、二つの問いによって、4つに切り分けられる。
- ■Aであり、Bである。A∩B・・・男であり、女である・・・(i)
- ■Aであり、Bでない。A∩¬B・・・男であり、女でない・・・(ii)
- ■Aでなく、Bである。¬A∩B・・・男でなく、女である・・・(iii)
- ■Aでなく、Bでない。¬A∩¬B・・・男でなく、女でない・・・(iv)
(i)を削除した世界は、左、(iv)を削除した世界は、右、
ここではじめて「包含関係」が成立し、
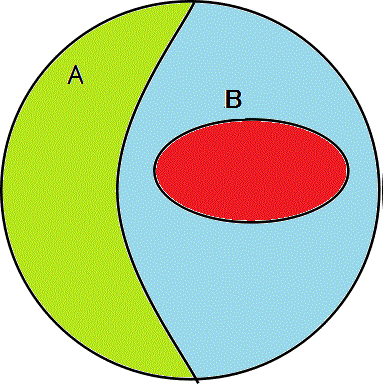
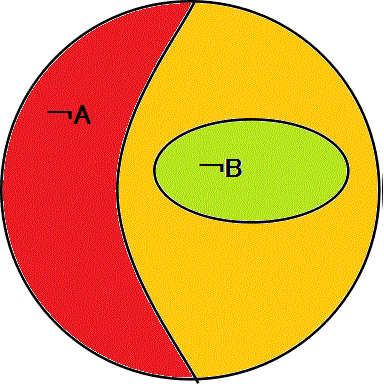
- 左図では、A∩B=φ、すなわち、AとBは「互いに素(共通の要素を持たない)」、「排反事象」であり、ここから、A⊂¬B、およびB⊂¬A、が帰結する。
このような「包含関係」が成立すれば、「Aであるならば、Bではない」、「Bであるならば、Aではない」という命題が、それぞれ「真」となる。
- 右図では、¬A∩¬B=φ、すなわち、¬Aと¬Bが「互いに素」、「排反」であり、ここから、¬A⊂B、および¬B⊂A、が帰結する。
このような「包含関係」が成立すれば、「Aでないならば、Bではある」、「Bでないならば、Aではある」という命題が、それぞれ「真」となる。
これらの場合に限・り・、「男?、じゃあ、女じゃないのね」、「女?、じゃあ、男じゃないのね」、「男じゃない?、なら、女ね」、「女じゃない?、なら、男ね」、
なる言明が成り立つのである。現実には、(i)と(iv)が、いかに少数であっても必ず、存在する。存在するなら、「包含関係」は成り立たないから、いずれの命題も、常に真とは言えない、「トートロジー」ではな・い・、のである。
「トートロジー」でないことを言ってはいけない、とは言ってない。「トートロジー」しか喋らない人がいたら、それは退屈、というものだ。「トートロジー」でな・い・、ことを言うことで、はじめて「意味」が生ずる。しかしここでその「意味」は、(i)または(iv)の、あるいは、その両方の、「排除」、ということになる。だから、暴力的だと言っている。論理的のみならず、ポリティカリーに、インコレクトだ、と言っている。
人間、という生き物の性別は、性染色体のxx型、xy型、のいずれかであるかを調べることで、「決定」できるのだろう。ただ、「自分は、・・・である」と思・っ・て・いるというのは、また別の事柄だ。
まるで、構造主義言語学の、「シニフィエ/シニフィアン」、「意味されるもの」と「意味するもの」みたいに(笑)、「二重構造」ができていて、だから、yes/no二つの答えしかない問いによっても、「世界」が、22=4つに、区分されてしまうのだよ。
日頃猫としか話をしない(笑)から、この「二重構造」を、言語由来のもの、言葉を獲得した人間固有のもの、と断ずるには抵抗がある。自分が猫だと思っていない猫がいそうな気もするし、ならば、自分が人間だと思っていない人間が、いてもいいはずではないか?
一番上の表で、「・・・でない」、「・・・である」を、「0/1」に割り当てたのは、のちに回帰直線、相関係数、などというものを算出するために、「答」が「数値」でなければならない、という便宜からではあるが、「1」、はじめの「順序数」、「ある」、「存在する」、「0」、その否定、「ない」、「存在しない」こと、と敷衍することもできる。電流回路の一か所にスイッチを設置すれば、それはon、とoffの二値しかとりえない。
これまた聞きかじり言語学、であるが、「有徴/無徴」、「しるしがあること」と「しるしがないこと」で、対立概念が表現される。「体制」と「反体制」、「首相」と「副首相」、「教授」と「准教授」、みたいに。「無徴」の方は、「○体制」、「○首相」、「○教授」の如く付加すべき記号が「欠如」している、足しても足さなくても結果が変わらない加法の単位元「0」のように、そこには、「ゼロ記号」が実は書き込まれているのだ、と考える。
日本語の「おとこ/おんな」の語源がどうなのかはよく知らない。英語なら、man/woman、male/female、he/sheと、「男」が「無徴」、「女」が「有徴」に割り当てられている。はじめに「無徴」があって、のちにそこに何かの「しるし」が書き込まれた、と「発生論」的に考えれば、「無徴」、「ゼロ記号」の方が、「元祖」なのであり、「本来」のものなのであり、「偉い」、ということになるだろう。「有徴」は、「本来」のものから、何かが「欠落」した態様だ、と解されることになる。
フロイト主義がフェミニズムから非難されたのは、女児のコンプレックスを説明するのに、「本来、あ・る・べ・き・はずの、おちん●んが、私にはない」などという論じ方をしたからだろう、と大雑把に理解している。
「ある」ことと「ない」ことの対立、という理解の枠組みは、あまりにも「合理的」だから、私たちの「意識」の隅々までいきわたり、反駁できないように思える。「彼には、実力があ・る・」、「彼には権力があ・る・」、というとき、私たちは、「実力」や「権力」を、目にしているわけではない。誰かが「彼」に、ぼこぼこにされているところを、目撃したり、想像したりすることで、そう、断ずるのである。
戸棚の上の茶碗が床に落ちて割れた。どうして割れたんだろう?、それは、ちゃぶ台の上の茶碗には「なく」、戸棚の上の茶碗には「ある」、何か、のせいだ。茶碗は、戸棚の上にあること、それのみによって「何か」を「持っている」!、こうして「ポテンシャル・エネルギー」概念が、生まれた!(笑)。
あまりにも「多様」なのでほぼ「ランダム」としか言いようのない、アミノ酸の配列、として存在している「私たち」は、この個体と、あの個体で、どちらがよりたくさん何かを「持っている」、などということは、あり得ない筈(笑)なのだ。市場に流通する貨幣量が一定だから、どこかが少なくなれば、どこかほかのところが多くなる、というアナロジーから生まれたのだろう(笑)、「エネルギー保存則」とは、別の理解の仕方が、あってもよかったはずなんだけどね。
この、架空の「調査結果」を用いて、「条件付き確率」に関する「ベイズの定理」、さらに、「独立性」といった話をしようと思った。めったに「人」と話をしないのに(笑)、たまたまそんな話をするチャンスがあったから、気になったのだ。前回は、調子に乗って、やや話が逸れ、読み返してみると、やや論旨も乱れているようだが(笑)、放置しておくことにする。

- x=1をA/x=0を¬A
- y=1をB/y=0を¬B
と名付ける。「ベイズの定理」は、次のようなものであるらしい。
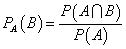
左辺、PA(B)は、Aがすでに生じたという条件のもとでのBの生じる確率、ということで、Aという条件のもとでの付いたBの確率、「条件付き確率」と呼ばれる。次のように書くこともできる。
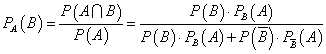
一番右側の辺の、分母の第一項は、Bが起こったうえで、Aが起こる確率、第二項はBが起こらなかった場合に、Aが起こる確率、それは合計すれば確かに、Bが起こると否とにか・か・わ・ら・ず・、Aの起こる確率P(A)を表しており、そして、分子は、分母の第一項と同じで、Bが起こったうえでのAの起こる確率、すなわち、AとBがともに生じる確率、と、読むことができる。
「確率」というのは、通常、さぁ、今からサイコロを振るぞ!、丁か半か?、・・・、ところで、過日、気になって「広辞苑」を引いたのだが、「丁」とは、課税対象となる成年男子、「一丁前」の語源はここにある、それともちろん無関係には思われないが、サイコロ賭博の「丁」は偶数even_number、「半」は奇数odd_number、なのだそうである、偶数こそが「十全」なものであり、奇数は、まさに「半端者」、ここにも成年男子をもって「十全」な人間とみる、「近代主義イデオロギーが、!」と息巻いていた次第である、閑話休題、・・・、というように、まだ生じていない「未来」についての予測にかかわるものであろうが、ここでは、「時間」の観念は消去されている。Aが生じてからBが生じたのか、はたまた、Bが生じてからAが生じたのか、AとBの「先後関係」は問わないのである。上の式の、AとBをそっくりすべて入れ替えても、成立するのである。
ここで挙げた「調査」の例でも、すでに「調査」は終了している。政権党の支持者であることも、選挙に投票したことも、薬を飲んだことも、病気が治ったことも、女であることも、タバコを吸うことも、みな、「過去」に属する事実である。いや、薬を飲んだか・ら・、病気が治ったのであって、薬を飲むことが「先」、病気が治ったことが「後」に決まってるだろう?、とおっしゃるかもしれないが(笑)、それこそが、ここで問題にしたい「独立性」の試金石なのであって、いや、実は薬を飲む前にすでに病気は治っていたのである、みたいな可能性をも考慮すると、そもそも「因果関係」があるとはどういうことなのか?、という、おなじみの(笑)話題に近づくのである。
おそらく、そんな「時間」への関心から、「条件付き確率」はまた「事後確率」とも呼ばれる。PA(B)は、すでにAが起こってし・ま・っ・た・上でのBの確率、それに対して、P(B)は、Aが生じると否とを問わない、Aが起こったかどうかわ・か・ら・な・い・段階での、Bの確率であるから、「事前確率」とも呼ばれる。だからもちろん、これは思考上の操作概念としての「前・後」であって、実際にAとBのどちらが先に生ずるかは、やはり、問題にしていない。
計算してみる。
- P(A)=20/60=1/3
- P(¬A)=40/60=2/3
- P(A∩B)=15/60=1/4
- P(¬A∩B)=27/60=9/20
- P(B)=42/60=7/10
- P(¬B)=18/60=3/10
- PB(A)=15/42=5/14
- P¬B(A)=5/18
- PB(¬A)=27/42=9/14
- P¬B(¬A)=13/18
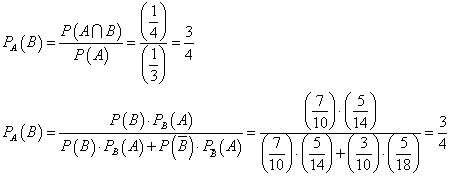
「政権党支持者のなかで、投票に行く人の割合」が15/20=0.75である、
「薬○○を服用した人のなかで、病△△が治癒した人の割合」が15/20=0.75である、
「女である人のなかで、喫煙者でない人の割合」が15/20=0.75である、
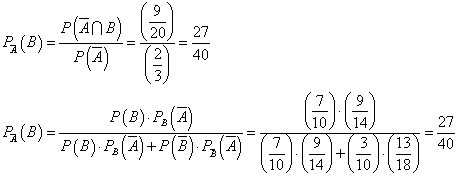
「政権党支持者ではない人のなかで、投票に行く人の割合」が27/40<0.75である、
「薬○○を服用したわけではない人のなかで、病△△が治癒した人の割合」が27/40<0.75である、
「女であるわけではない人のなかで、喫煙者でない人の割合」が27/40<0.75である、
そして、ほかならぬ、この「事後確率」PA(B)と、P¬A(B)との値が異なり、
PA(B)>P¬A(B)
Aがすでに生じた場合に、Bであることの方が、Aが生じないときに、Bであること、より、起こりやすい、
そこから、それぞれ、
「投票結果は、実・際・の・、政権党支持率を、多めに、見積もっている」、
「薬○○を服用することで、病△△の治癒の可能性が高まる、つまり、薬○○には薬効がある」、
「女の人の方が、喫煙者でない可能性が高い」、
という結論を下すことができる、ことになる。
両者がぴったり同じ値、PA(B)=P¬A(B)ならば、何が言えるのだろう?
このときは、当然にも、PA(B)=P¬A(B)=P(B)が成立する。事前確率と事後確率が等しいのである。
「政権党支持者であるかどうかと、投票に行くかどうか、とは、関係がない」、
だから、例えば、「雨が降って投票率が下がれば、政権党に有利」などとの予測はできない、
「薬○○を服用することと、病△△が治癒する、こと、とは、関係がない」、
したがって、それは、既に、「薬」では、ない、もちろん、「毒」でもないが、
「女であるかどうかと、タバコを吸うかどうか、とは、関係がない」、
私は、14年前に喫煙をやめた、ありがちなことだが、かつての「ヘビースモーカー」は、喫煙者を「憎む」(笑)もので、今では、すれ違いざま相手からたばこのにおいがすることにすら、やや苛立ったりする、のだが、例えば、廊下の向こうから近づいてくる人物が、男であるか女であるかによって、タバコのにおいがするか否かの、「期待」が変わってくる、ということが、ない、という、
それぞれ、結論を下す、または、結論が下せな・い・、ことになるのである。
この事態をもって、Aであることと、Bであることとは、「独立である」、と称する。
したがって、「独立性」の定義は、PA(B)=P¬A(B)=P(B)、であり、
この式と、
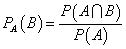
から、
P(A∩B)=P(A)・P(B)
が帰結する。これを、A、Bが「独立」である場合の、確率の「乗法定理」という。
「私たち」は、例えば、サイコロを2回投げて、2回とも「6」である確率は、と問われて、ああ、それなら、1/6×1/6で1/36ね、と答えるとき、「乗法定理」を使用している。例えば、昨年までの「旧課程」での大学受験生は、「条件付き確率」も、「独立性」の定義も、学んでいない、にもかかわらず、である。
二つの物事に、「関係がない」という事態を、私たちは、「直感的に」知っている。サイコロを2回振るとき、一回目に6が出たから、二回目には6が出にくい、と、冷静に考えれば、思わない。
サイコロのたとえをやめて、「1」から「6」の数字が書かれた、6枚のカードの話にしよう。箱の中に6枚のカードを入れて、一枚抜き取る。ああ「6」だった、引いたカードを再び箱に戻して、もう一度引く、これを「復元抽出」と呼ぶ、当然、何回繰り返しても、「6」が出る確率は、1/6であろう。
すでに引いたカードを元に戻さないなら、1回目に「6」が出たなら、2回目に引くときにもはや「6」が出る確率は、0となる。これを「非復元抽出」と称す。「非復元抽出」では、
一回目に「6」が出ず、二回目に「6」が出る確率は、
5/6×1/5=1/6
一回目にも二回目にも「6」が出ず、三回目に「6」が出る確率は、
5/6×4/5×1/4=1/6
一回目にも二回目にも三回目にも「6」が出ず、四回目に「6」が出る確率は、
5/6×4/5×3/4×1/3=1/6
一回目にも二回目にも三回目にも四回目にも「6」が出ず、五回目に「6」が出る確率は、
5/6×4/5×3/4×2/3×1/2=1/6
最後に(笑)、一回目にも二回目にも三回目にも四回目五回目にもにも「6」が出ず、六回目に「6」が出る確率は、
5/6×4/5×3/4×2/3×1/2×1/1=1/6
と、いつまでたっても、確率は変わらない。6本のうち1本が当たりくじてあるくじを6人が引くのに、どんな順番で引いても、「期待」は同じだ、という、いささか常識に反する結論となる。いささか禍々しいたとえだが、「ロシアン・ルーレット」で、誰が先にピストルを手にするかに、ほかならぬ「私」が死ぬ可能性は依存しない、というのである。もちろん死にたくなかったら、順番が後の方が望ましい、もちろんそれは、「時間」の観念を盛り込んでいるから、もはや、「確率」の概念は、それにこたえてくれない、ということなのだろう。
また、話が逸れたが、ここに、すでに「ベイズの定理」が用いられているのであるが、二回目にカードを引く際に、その「前」に、「6」が出たか否かは、次に「6」が出るか否かに、大いに影響を及ぼす、二回目の確率の算出が、一回目の結果に「従属」dependentしている、だから、「独立」independentでは、ない、ということになるのである。
「関係がない」という事態を、統計学の言葉では、「相関がない」ともいう。そこで、では、「独立」であることを、回帰直線の係数、や、相関係数、で表現するとどういうことになるのか?、と、次回は、そんな話をする予定。
二つの変量x,yの間に、「相関」があるか否かを見るには、まず、横軸x、縦軸yの座標に、変量のそれぞれの値(x1,y1),(x2,y2),・・・,(xn,yn)を、「点」としてプロットしてみる。それらの「点」の雲状の集まりが、
- 右肩上がりであるならば、「正の相関」、xが増えれば、yも増える、
- 右に向かって下がっているならば、「負の相関」、xが増えれるほど、yは減る、
- 横軸にほぼ平行であれば、「相関がない」、xの増現は、yの増減に無関係、
と言うことができる。もう一つ、「点」のかたまりが、予想される直線のまわりに、
- 密集していたら、「強い相関」、相関関係について、より断定的にものが言え、
- バラバラに散らばっているようならば、「弱い相関」、相関が認められたとしても、あまりはっきりしたことが言えない、
ことになる。これらを、客観的に表示する指標が「相関係数」rで、その定義式は、「最小二乗法」と呼ばれる手法で、「回帰直線」を求めるプロセスから得られる。
座標上にプロットされた点の集まり、これを「散布図」というが、各点がそのまわりに並んでいる、と想像されるある直線を、y=ax+bと仮定して、与えられた変量xの各値、xiから予測されるそのy座標、axi+bと、真の値、yi、との「ずれ」を積算し、その積算値が最小となるようなa、bを発見する、というわけである。
「ずれ」はプラスであることもマイナスであることもありうるから、そのまま足せば打ち消しあってしまう、こういうとき統計学は常道として、その二乗の和をとるわけである。のちの計算の便宜もあって、これを、各点についての平均的な「ずれの二乗」ということで、個数nで割っておく。
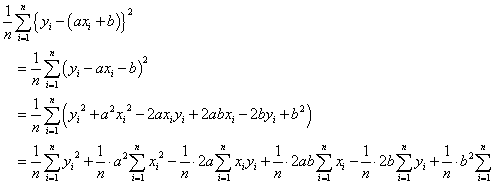
ここで、変量x、yの「平均」は、それぞれ、
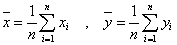
「分散」は、分布の広がり具合を評価するもので、「偏差(平均値との差)の二乗の平均値」、と定義されるが、そこから次の式が得られ、
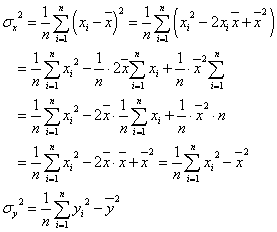
「『二乗の平均』-『平均の二乗』」であることがわかり、
「共分散」は、「(2変量の)偏差の積の平均値」が定義だが、同様の変形で、
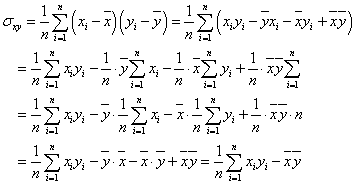
「『積の平均』-『平均の積』」であることがわかり、では、これらを用いて、先の、直線との「ずれ」の式を変形すると、
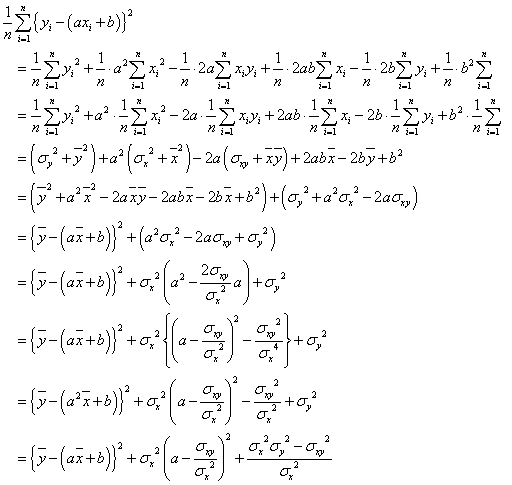
後ろ4行ばかり、右側の項では、aについての「平方完成」をしているのである。最後に残った3項は、すべて正値である。前2項は実数の二乗だから当然、第3項の分子は、分散の積から、共分散の二乗を引いている、共分散は、正負の要素を含んでいるから、その絶対値は、分散の積の平方根、つまり、標準偏差の積より、小さくなりそうである(笑)、証明には、あるいは「シュヴァルツの不等式」を用いるかもしれない、いずれにせよ、では、この、直線からの隔たりを、最小にするのは?、と問われれば、前2項が同時にゼロになる場合だ、と断言できることになろう。

こうして、「回帰直線」y=ax+bの係数が定まった。
傾きaが、正であるならば、「正の相関」、負であるならば、「負の相関」、分母xの分散、は正に決まっているから、したがって、相関の正負は、「共分散」の正負によって決まる。
では、「相関の強さ」は何によって判定するか?、当然、「回帰直線」との隔たりの大きさ、すなわち、上式の前2項がいずれも0となった場合においてもなお残る、第3項であろう。これも分母は正であることははっきりしているから、分子を次のように変形する。
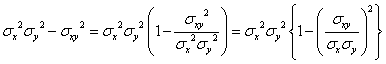
ここで、「相関係数」rとして、
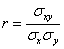
と定義すれば、右辺の中カッコの中身は、(1-r2)=(1+r)(1-r)、
これは、x軸と(-1,0)および(1,0)で交わる上に凸の2次関数、であるから、rが-1,1に近づけば、「ずれ」は小さくなり、0に近づくほど、「ずれ」は大きくなる。まさにこのようにして、「相関の強さ」を表示していることがわかる。
本日はこれまで。
ここで材料にしている「架空の」調査結果は、yes/noの二値しか取れない、二つの問いであるから、60人のサンプル(標本)に対して、
(x1,x1),(x2,x2),・・・,(x60,x60)
の答えのセットがあるが、それらはすべて、(0,0),(0,1),(1,0),(1,1)のいずれかであるから、座標上にプロットしてみても、重なってしまってその配置の傾向、など、読み取れるわけがない。ただ、形式的にはこのようなデータでも、回帰係数や、相関係数を求めることができ、そこから、何らかの「結論」を引き出すこともできるはずだ、それを確認したかったのである。
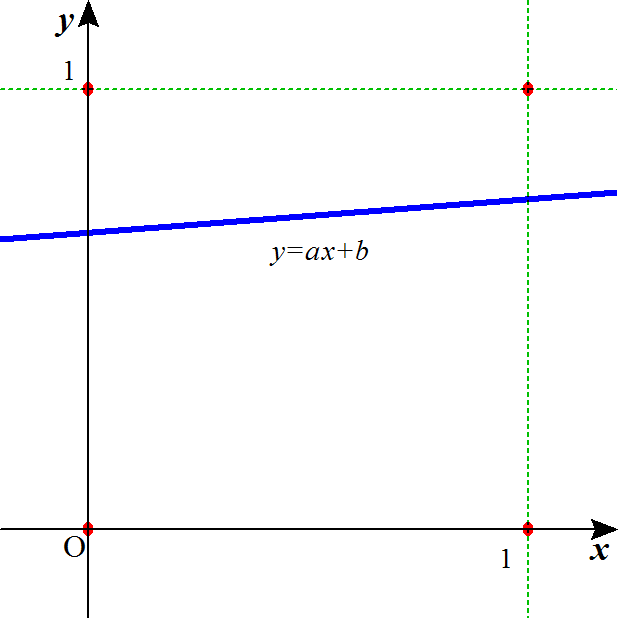
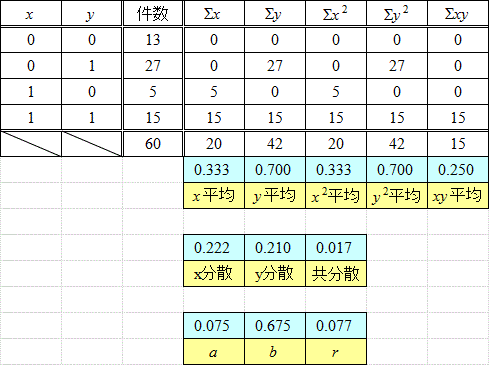
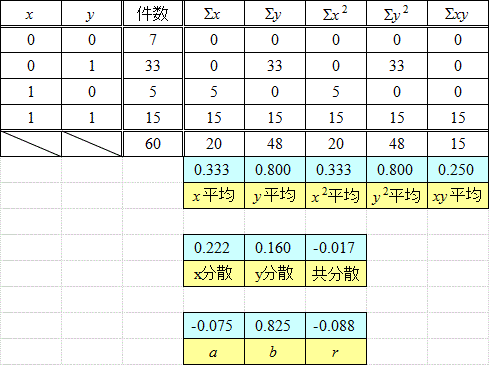
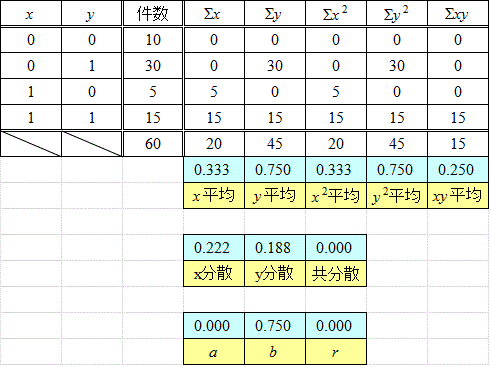
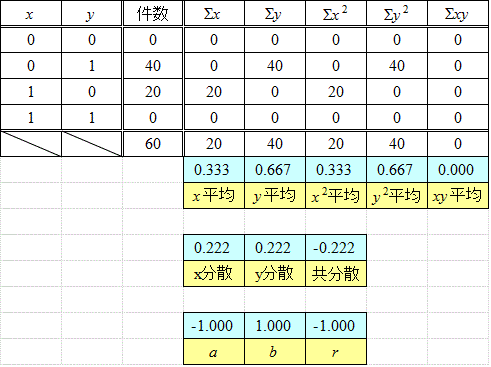
まず、前に挙げた「調査結果」の場合。大げさな数表を掲げているが、計算は楽なものである。回帰直線の傾きa=0.075わずかに右上がりであるから「正の相関」であるが、相関係数r=0.077、こんなもの、ほとんど「無相関」であるから、こんな調査結果からは、何も言えない、言ってはならない、いや、「何も言えない」という結論が得られた、と言って「よい」。
回帰直線のy切片b=0.675、は、何を意味しているのだろう?、2点(0,0)と(0,1)とを、x=0であるときのy=1/0の配分27:13に、「内分」して(0,0.675)、同様に、(1,0)と(1,1)を15:5=3:1に内分した点は、(1,0.75)であるから、直線は、これら2点を通り、その傾きは、
(0.75-0.675)/(1-0)=0.075
なるほど、これが回帰直線の傾きaなのであった、考えてみれば、理の当然(笑)、であったわけである。

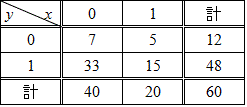
ちょいとデータを加工して、「負の相関」の場合を作ってみた。
- x=1をA/x=0を¬A
- y=1をB/y=0を¬B
とすれば、
P(A)=20/60=1/3
P(A∩B)=15/60=1/4
PA(B)=15/20=3/4
ここまでは、上のデータと同じだが、
P(¬A)=40/60=2/3
P(¬A∩B)=33/60=11/20
P¬A(B)=33/40>3/4
ということになって、Aであるもののうちの、Bであるものの確率、より、Aでないもののうちの、Bであるものの確率の方が、大きい、
「政権党支持者ではない人のなかで、投票に行く人の割合」が33/40>0.75である、
「薬○○を服用したわけではない人のなかで、病△△が治癒した人の割合」が33/40>0.75である、
「女であるわけではない人のなかで、喫煙者でない人の割合」が33/40>0.75である、
ここから、
「投票結果は、実・際・の・、政権党支持率を、少・な・目・に・、見積もっている」、
「薬○○を服用することで、病△△の治癒の可能性が低・く・な・る・、つまり、薬○○には薬効がない、どころではなく、むしろ治癒を阻害している、『毒』だと言ってもいい」、
「女の人の方が、喫煙者である可能性が高い」、
との結論になるが、もちろん、ここでも相関係数は極めて0に近く、むろん、そう確定的なことが言えるわけではなかろう。
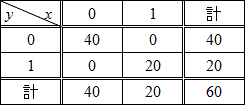
これら二例は、いずれも、「事前確率」と「事後確率」が、わずかであっても異・な・っ・て・い・る・から、Aであることと、Bであることとが、「独立ではない」、場合であったが、では、どんな調査結果であったら、「独立性」を帰結できるのか?、次のようなものである。
PA(B)=15/20=3/4
P¬A(B)=30/40=3/4
P(B)=45/60=3/4
なるほど、「事前確率」と「事後確率」が等しい、Aであってもなくても、Bである確率は変わらない。だから、「乗法定理」も成立するのである。
P(A)=20/60=1/3
P(B)=45/60=3/4
P(A∩B)=15/60=1/4
したがって、
P(A∩B)=P(A)・P(B)
で、回帰直線の傾きa=0であることが、「独立であること」に対応していることがわかった(笑)のである。
回帰直線のy切片b=0.75は、2点(0,0)と(0,1)を3:1に内分した点(0,0.75)に対応している。これと、2点(1,0)と(1,1)を3:1に内分した点(1,0.75)をつなげば、真横、x軸に平行な直線が得られるのもまた、理の当然であった(笑)。
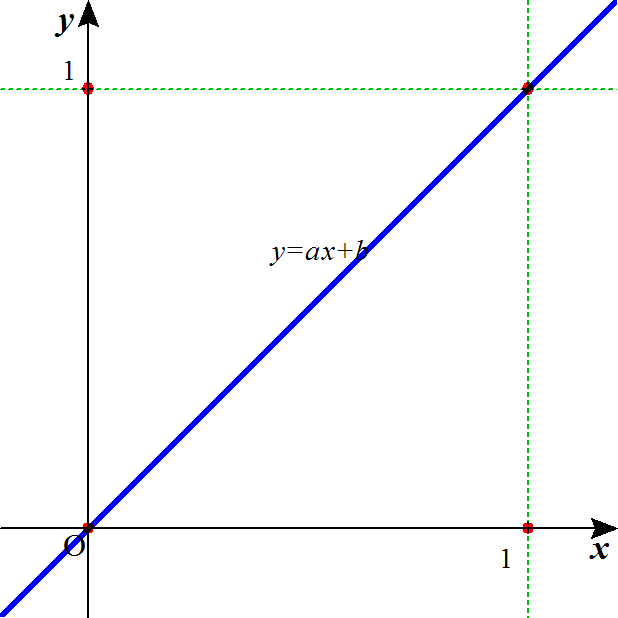
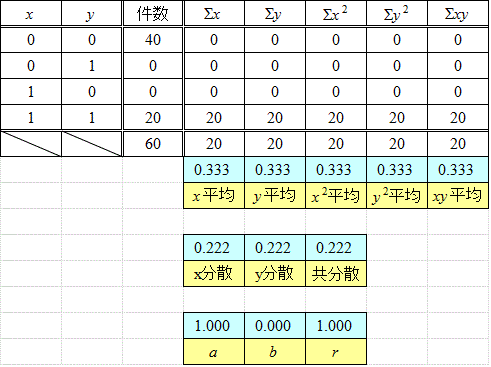
一方の極端が、完全な「独立性」であるなら、他方の極端は、完全な「従属性」、一つは、こんな形、極めて強い、正の相関、
「政権党支持者だけが投票所に行き、たった一人しかいない候補者の名前を書いてくる、反対派はプロテストとして、全員棄権する、政府は、得票率100パーセントで当選、と発表する」、そんな感じかな?
「薬○○を服用した人は病△△がが全員治癒、服用しなかった人は、誰一人治癒しませんでした」、製薬会社は、薬事法上、「この薬は効きます」という広告をしてはいけないんだそうだが、サプリメントや健康食品にはその規制は及ばないので、通販広告にはありそうな文言だが、もっとも、「ご利用いただいた方の97パーセントの方から『満足している』とのご返事をいただいております」みたいな広告は、「統計学的」には、誤っている、と言われる、「ご利用」していない人の調査結果を得ることはできないし、例えば、商品に添付されている葉書をわざわざ返送するような人は、もともとその商品に好意的だ・っ・た・、と推認され、「こんなもの、ちっとも効かないじゃないか!」と怒っている人は、葉書もろとも破り捨てているだろう、ことも予想できるからで、そもそも「標本」抽出の過程に、「偏り」があるのである。
「女である人は、全員喫煙者で、女でない人は、だれもたばこを吸わない」、
「現実に」ありそうかどうか?、ということを離れて、こういう場合に限・っ・て・、私たちは、「○○ならば、▽▽である」という結論を下せるのだ、と、まあ、強調したいわけである(笑)。
もう一つは、もちろん、極めて強い、負の相関。いささか、飽きてきたので、もう、例を挙げることは、しない(笑)。
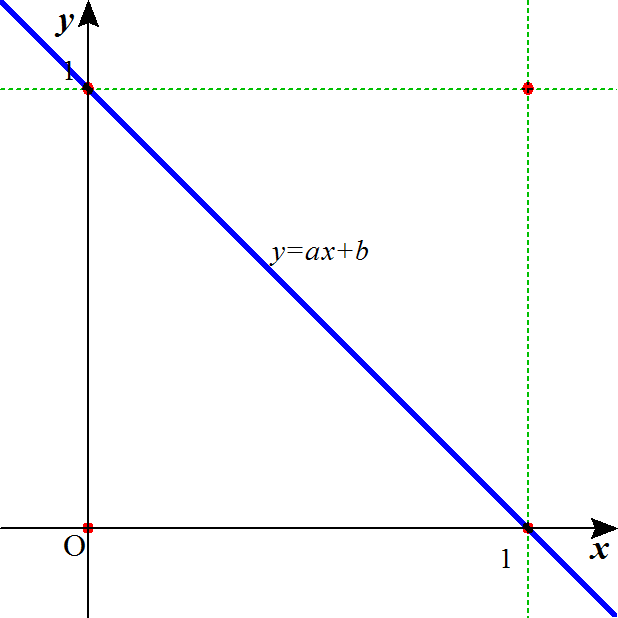
「誰のせいだとか、関係、ないっ〜♪」
と、モンゴル800は歌った(「矛盾の上に咲く花」、「message」所収)のだが、「誰かのせ・い・だという」、「何者かの『責任』に帰す」というのは、あるいは、「ああしたか・ら・、こうなった」という「因果」を論じるのも、いわば「従属性」を前提としているのであって、
こうして、何度も何度も繰り返し、同じテーマになるのだが、
- 努力したから金持ちになった、なら、嗚呼、私が金持ちじゃないのは、努力が足りなかったのだ、
- 勉強したから、合格できた、なら、嗚呼、私が合格できなかったのは、勉強しなかったからだ、
- 「愛」の豊かな環境で育ったから、「健全」な人間に育った、なら、嗚呼、私が「ゆがんだ」大人なのは(笑)、「愛」が足りなかったからだ、
とは、絶対に、言いたくないから、それは、資本主義勃興期のプロテスタント・カルバン派の「罪悪感」に基づくイデオロギーなのだ、などと、カルバン派には申し訳ないが、そんな悪態をついてみるのも、「愛着障害者」かもしれない「私」が、「ゆがんだ」ままでも生きていてよ・い・、猫のびー♪ちゃんが、下半身不随でも、生きていてよい、犬のペペ♪ちゃんが、うんこ、しっこ垂れ流しでも、生きていていい、のと同様に、・・・、ことを立証したいからなのであって、嗚呼、それにしても「関係、ないっ!」というのは、なんとすがすがしい言明であろう!
世界はランダムに、「多様に」、できているから、完全に「独立」、も、完全に「従属」、も「実際」には、当然、あり得ない。
完全な「独立性」から、どれほど隔たっているか?、ということを言うために、統計学の世界では、「カイ二乗検定」なるものを行うらしいのである。「カイ」は、確かギリシャ文字「χ」、数学で未知数のことを「エックスx」とするのは、この文字のある種の「読み間違い」であるらしい、また、かつては「根root」と呼ばれた方程式を満たす値のことを日本語で「解」と呼ぶのは、「χ」の語呂合わせでもあるらしい。
正規分布に従う変量の2乗の値を加算すると、それは「カイ二乗(χ2)分布」に従うことが知られている(笑)、らしい。統計学の教科書、延々数ページにわたる数式変形をたどるのは、今は、ちょっと無理で、そういえば、正規分布確率密度関数の話も、頓挫したままになっている!、不本意だけれども(笑)、「公式」だけを流用して、上の例に、適用してみたい、と思う。それともう一つ、これはずいぶん前に読んだ本だけれども、「推計学のすすめ」佐藤信(講談社ブルーバックス)に載っていた、手計算で簡単にできそうな「直接法による独立性の検定」、も、できるかどうかわからないが、やってみたいと思う。
さて、以下の架空の調査結果、
- x=1をA/x=0を¬A
- y=1をB/y=0を¬B
として、Aであることと、Bであることが、無関係である、すなわち「独立」である、のか、それとも、AであるならBでありやすい、もしくは、AであるならBでありにくい、との、関係がある、すなわち「従属」であるのか、むろん、「完全な独立」でも、「完全な従属」でもないことは、既に分かっているから、独立と従属との間の一体、ど・の・あ・た・り・に・位置しているのか?、を、知りたい、いや、本当に「知りたい」わけでは、たいしてないのだが(笑)、そうして、気分を盛り立ててみよう、というわけである。

「直接法」という、どうも、数理統計学的な分布、などの数式を必要としないことが「直接」の意らしいが、の、方が説明しやすそうなので、そちらから入る。
このデータを前提として、Aである確率P(A)が20/60であり、Bである確率P(B)が42/60である、ことを所与の拘束条件とする。例えば、「薬を飲んだら治った」例なら、現実に、60人中20人に投薬し、現実に、60人中42人が治癒した、というのが動かせない事実としたときに、ほ・か・な・ら・ぬ・、このような数値の配分が生じるのは、まったくの偶然、と言うべきなのか?、それとも、いや、非常にありそうなこと、と言うべきなのか?、という問題の立て方をするらしい。
つまり、この数表の「計」の欄、縦、横を動かさずに、内側の4桝を変化させてみて、いろいろ、あ・り・得・た・他の場合を考えてみるに、たとえば、左上欄¬A∩¬B、「薬も飲まず、治りもしなかった人数」を、kとすると、ほかの3枡は、自動的に決まってしまう。
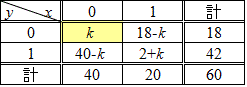
kには、0,1,2,・・・,18のいずれかが入るが、このように「自由に」選ぶことのできる変数が、ただ一つであることが、のちに紹介する「χ2検定」の際の「自由度1」の意味なのだ、と、想像している。
では、このように、kに19通りの様々な数値が入る、膨大な場合の数のうち、ほ・か・な・ら・ぬ・上記調査結果が生じる確率は、いかほどものであろうか?
もちろんおなじみの話題であるが、調査対象の60人は、ゆめゆめ「区別のできない赤玉」では、ない。すべて「名」をもち、識別でき、「順序数」に対応付けられたからこそ、数えられたのである。では、その「名」、例えば「sample(標本)」のsとして、s1,s1,・・・,s60、
- この60人から、まず、k人選ぶ、・・・60Ck
- 残り(60-k)人から、(18-k)人選ぶ、・・・60-kC18-k
- 残り42人から、(40-k)人選ぶ、・・・42C40-k
- 残り(2+k)人から、(2+k)人選ぶ、・・・2+kC2+k
このような選択作業は、それこそ「独立」であるから、「乗法定理」が成立し、上の各場合の数の積が、例えば「薬も飲まず、治りもしなかった人数」が、kであった場合の数になる。ならば、この拘束条件の下での、すべての場合の数は、
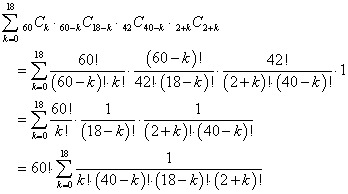
これに対して、ほかならぬ、k=13であった場合の数は、
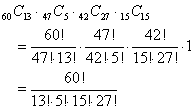
となる。これはもちろん、途方もない計算である。「直接法」は、元来、もっとサンプル数が少ない場合、手元に精緻な統計表がない場合でも、技術者が「現場」で暗算、電卓程度で計算できる便法、なのだと思われるから、こんな使い方は邪道なのであるが、聞きかじりの「χ2検定」だけでは心もとない(笑)ので、やってみたまでである。この程度の計算なら、Excel、いや、その「バッタもん」King●oftSpreadSheetでもできるようであるし。結果は、「χ2検定」とともに、次回へ、・・・。
***
前回の、「χ(カイ)」に関する薀蓄(うんちく)、もちろん、言わずもがな(笑い)なことであるのだけれど、言い忘れたことがあった。この文字に該当するラテン語のつづり字は、確か、quoiみたいな感じで、うんちくの割には不正確であるが(笑)、ラテン系諸語では、疑問詞、関係詞は、quで始まるものが多く、ゲルマン系の英語ならwhにあたるところだが、だから、「何かわからないもの、未知数」だからこそ、「χ」だったわけだ。questionって言葉、英語でtionは、「ション」という発音になる、stationみたいに、のが通例なのに、これだけは、「クエスチョン」が正しい、と言われるのは、これがフランス語からの外来語だからだ、と言われる。
この以下の架空の調査結果、

- x=1をA/x=0を¬A
- y=1をB/y=0を¬B
として、Aであることと、Bであることが、「独立」であるか「従属」であるか、を見るのであった。
Aであるものが20、従ってAでないものが40、Bであるものが42、従ってBでないものが18、この事実を「所与」givenのものとして固定すると、以下の表のように、中央部の4コマ、二つのyes/noの問いで構成されているから、「2×2分割表」と呼ばれる、は、そのどこか一つのコマ、例えば左上(x,y)=(0,0)をk=0,1,2,・・・,18の19通りの数字から一つ「自由」に選べば、他の3コマは、「決定」されてしまう。これが「自由度1」の意味だ、と、思う。という話はした。
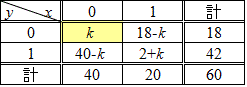
では、「独立性に関するχ2検定」を、始めさせていただく。三十数年前の数理統計学の教科書や、その他入門書の類を繰ってみても、結局、どうして、以下に示す「独立性との食い違いの測度」、がχ2分布に従うのか?、は、他人様に説明できるほどには、理解できなかったから、ここでは、「へぇ、そういうものなんだ」と、ただ、淡々と、「公式」に適用して作業を進める、という体裁になる。
こういうとき、当代の人々は、しばしば、「粛々と」ことを進める、と言いたがるようなのだが、一度「広辞苑」でも引いて見られればよい。
「粛々」、(1)つつしむさま。(2)静かにひっそりしたさま。(3)ひきしまったさま。(4)おごそかなさま。
反対者が多数を占めていることが、「投票」という標本調査によって明らかになったのちも、警備艇で海上を封鎖し、抗議者を検束して工事を進めるとするならば、それを、「粛々」とは、言わない。
何の話をしている?、「帰無仮説」という言葉があって、それは文字通り「『無』に『帰する』べく設定された仮説」、「棄却される」ことが目的であるような仮説、「背理法」のロジックにも似て、
「もし、○○だとしたら、と仮定する。その上で計算してみると、いや、そんなことは、非常に低い確率、5パーセント未満、とか1パーセント未満、でしか起こりえない、ことがわかる。ならば、残念であるが(笑)、○○である、との仮説は捨てなければ、棄却されなければならない。だから、○○でな・い・ことが、わかったのである。」
ということであるらしい。
ここでも、もし「所与」の拘束条件、Aが20、Bが42を固定したうえで、次のような「帰無仮説」を立てる。
仮説:AとBは、「独立」である。
この条件の下で、AとBが「独立」であるとしたら、
PA(B)=P(B)
であるから、14/20=42/60、下の表のようでなければならなかったはずだ。
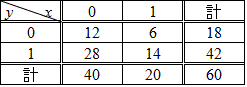
ところが、「現実」には、こうはなっていない。そこで、「現実」と、「仮説」すなわち「独立」との、「隔たり」を示す指標が求められる。
「独立性との食い違いの測度」は、次のように定義される。

ここでのΣ記号は、この「2×2分割表」の4コマすべてについての和、を意味する。
- (x,y)=(0,0)では、実測値13、理論値12、
- (x,y)=(0,1)では、実測値27、理論値28、
- (x,y)=(1,0)では、実測値5、理論値6、
- (x,y)=(1,1)では、実測値15、理論値14、
であるから、「独立性との食い違いの測度」は、
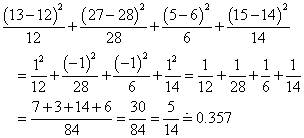
これが、「自由度1のχ2分布」に従うことが知られているので、・・・、χ2分布を表す数式は、私自身が理解していないので(笑)、挙げない、ずいぶん古いバージョンの「Excel関数マニュアル」をもっているので、「χ2分布」だろうが、「F分布」だろうが、「T分布」だろうが、しかるべきパラメータを代入すれば、たちどころに計算してくれるこはを知っていたのに、試みに「help」で「χ2分布」と、問い合わせても、「そんなものは、ないっ!」みたいな返答なのであるが、仕方なくセルに「=chidist(■■,1)」、■■はセル番地、と入力すると、こともなげに、計算してくれるので、この「ヘルプ・ファイル」は、「自分ができること」を「自分」が知・ら・な・い・、のか、あるいは、知っていても面倒くさいから、答えない、のか、いずれかであることが、わかった、次第である、が、・・・、そのようにして作成した「自由度1のχ2分布」を下に掲げる。
横軸が「独立性との食い違いの測度」で、縦軸がその「確率」である。
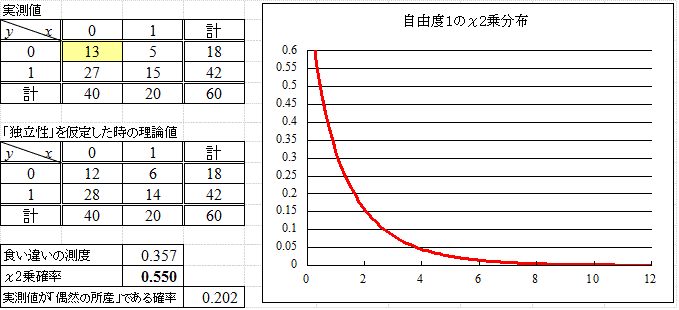
さて、「独立性との食い違いの測度」0.357が生ずるような確率は、0.550、5割以上も起こる、というのは、極めて「平凡」な事柄であることは理解されよう。何が言えたのか?、「独立性」との「食い違い」が、あまりにも小さいので、そんなことは、ままあることだ、だから、ほとんど、「独立」と言って、よい、・・・、なんと「帰無仮説」を「無」に「帰す」ことができなかった、のである。
前回紹介した「直接法」による帰結も、合わせ述べておく。ここでの「帰無仮説」は、
仮説:所与の条件の下で、ほかならぬこのような「2×2分割表」が得られたのは、まったくの偶然の所産である」、
になる。所与の条件を満たしながら、ありうるすべての場合に対する、ほかならぬこの配分である確率は、0.202、2割「も」ある、というのは、やはりそんなに珍しいことではない。だから、この仮説も「棄却」されない。つまり、こんなことは「偶然」なのだ、何か「裏」がある、とは言えない、何か「関係、従属性」があるとは、言えない、つまり、「独立」なのだ!
これでは「オチ」がつかないので、めでたく「帰無仮説」が棄却されるように、データを加工してみた。
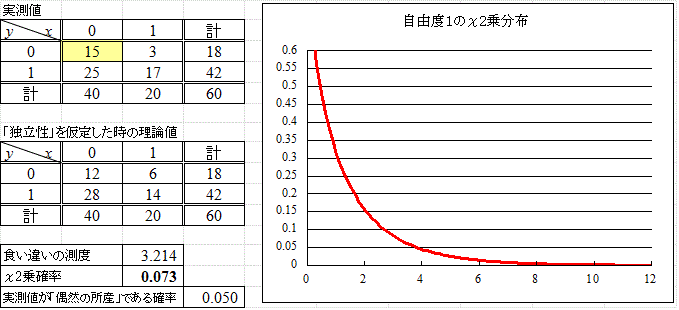
「独立性との食い違いの測度」が3.214と、かなり大きくなってきて、こんなことが起こる確率は、7.3パーセントくらい、ならば、「独立である」という仮説は、やや、怪しくなってくる、し、
この配分が生じる確率も、5パーセント、というのだから、なかなか、「偶然の所産」とも言えなくなってきた。
これは「限界事例」であろう。統計学が「信頼区間」をしばしば95パーセント、にとる根拠を、私は正確に述べることはできない。想像するに、「中心極限定理」により、すべての分布が、究極的には収束する、と言われている「正規分布」の、平均値プラスマイナス2標準偏差、m±2σ、のレンジに収まるデータが、くしくも、ほぼ、95パーセントであるという事実、「世界」は、95パーセントの、「正常」、「まとも」、「普通」、と、「残余」の5パーセント、の「異常」、「逸脱」、「例外」、でできている、というコンセプトに由来するのであろうか?
それでは、というわけで、露骨に5パーセントを下回るデータをねつ造してみると、
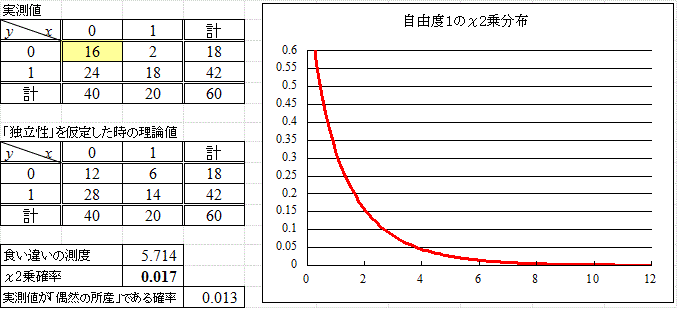
これなら文句はあるまい。
これほどまでに「独立性との食い違いの測度」が大きい事態は、1.7パーセントしか起こりえない。だから、「独立である」との仮説は棄却される。AとBは「独立」でない、すなわち「従属」である、AならばB、BならばA、と述べる根拠が、ある。
「政権党」支持者の方が、より多く投票所に行く、
薬○○を服用したものの方が、病△△から治癒しやすい、
女である、者の方が、喫煙者でない、と予想できる、
と、言ってよい。「直接法」の結果からも、
この数値の配分が、まったくの「偶然」であるとは、とても思えない、なぜなら、そんなことは、1.3パーセントの確率でしか起こりえないからだ、だから、「偶然」では、ない、何か、「裏」が、ある、つまり、Aであることと、Bであることとの間には、「関係」が、ある!