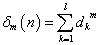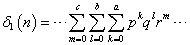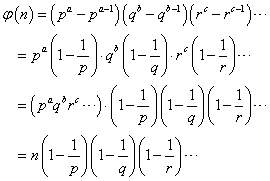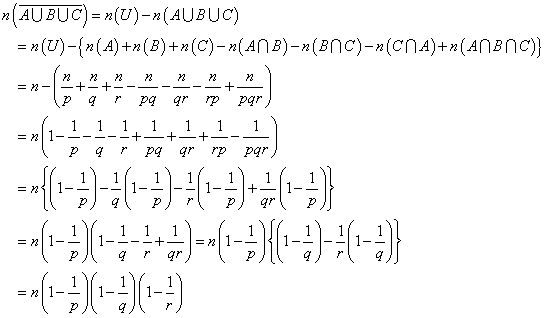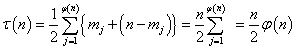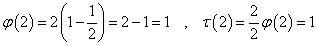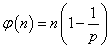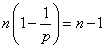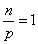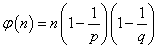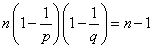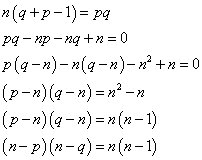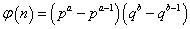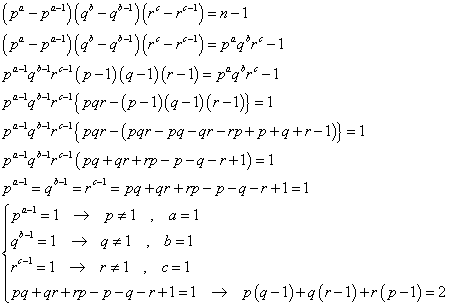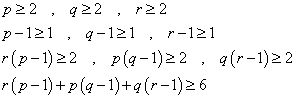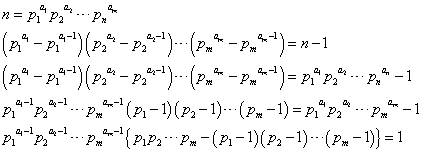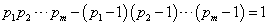「群の公理」、「環の公理」、「体の公理」を探して「素数」芹沢正三(講談社ブルーバックス)を渉猟しているうち、またしても聞き覚えのある「オイラー氏」の名前が出てきたので、思わず、没頭してしまったのであった。
- 自然数nの正の約数d1,d2,d3,・・・,dlに対して、これらのm乗の和を、δm(n)と定義する。
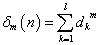
すると、これは、m=0のとき、「自然数nの正の約数の個数」を、m=1のとき、「自然数nの正の約数の和」を、それぞれ表すことになる。まるで、数理統計学で出てきた「積率」と同じ考え方だ!
ところが、こう表記したからとて、特に計算が楽になる、などと言う事情は、見つけられないのだが。
- δ0(n) : 自然数nの正の約数の個数
nの素因数分解を、n=paqbrc・・・とすると、
nの正の約数は、ことごとく、pkqlrm・・・
ただし、
k=0,1,2,・・・,a、
l=0,1,2,・・・,b、
m=0,1,2,・・・,c、
・・・、
とあらわされる。すなわち、
kと書かれた「箱」から、0,1,2,・・・,a、と書かれたa+1個の「ボール」を選び出し、
lと書かれた「箱」から、0,1,2,・・・,b、と書かれたb+1個の「ボール」を選び出し、
mと書かれた「箱」から、0,1,2,・・・,c、と書かれたc+1個の「ボール」を選び出し、
・・・、
という作業によって得られた結果と、「nの正の約数」一つ一つは、「一対一対応」する。だから、数え終わった結果、得られた個数、「カーディナル数」は等しく、だから、話を「ボール選び」に「すり替えて」も、かまわないのである。
pの選び方、qの選び方、rの選び方、・・・、は相互に「独立」である。だって「箱」が違うのだから。「独立」だから、「乗法定理」が成り立ち、これら、3つの場合の数、a+1、b+1、c+1、を、かければ、すべての場合の数が得られることになる。
こうして、
δ0(n)=(c+1)(b+1)(c+1)・・・
が得られた。ここで「独立」だから、「乗法定理」が使える、という議論が、この関数δ0(n)が「乗法的関数」である、という議論になるらしいのだが、あまりうまく納得できなかったので、それは省略。
- δ1(n) : 自然数nの正の約数の和
同じく、nの素因数分解を、n=paqbrc・・・とすると、
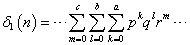
と書けるであろう。これは、次のように変形できるはずだ。

ここで、Σ記号の変数を含んでいない項を、そのΣ記号の外(前)へ放り出しているが、それが、「独立」であることに対応し、したがって、δ1(n)もまた、「乗法的関数」(その関数による演算と掛け算とが交換可能であること)である、と言えることに対応しているのだと思われる。
この式に現れた輪は、左から順に、
初項1、公比r、項数c+1、の等比数列、
初項1、公比q、項数b+1、の等比数列、
初項1、公比p、項数a+1、の等比数列、
であるから、

- 自然数nと、互いに素な、n以下の自然数の個数を、φ(n)とする。
これを「オイラー関数」と呼ぶ。
- nが、ただ一つの素数pのべき乗でできている場合を、まず、考える。すなわち、n=pa、
自然数を1からnまで順に並べたところを想像すれば、n=paと「互いに素でな・い・」ものは、p個ごとに、現われるであろう、
ならば、その個数は、pa/p=pa-1であろう?、ならば、paと「互いに素であ・る・」ものの個数は、全体nからこれを引き、
n-pa-1=pa-pa-1
となるであろう。
- これを一般の場合、nが多数の素因数をもち、その素因数分解が、n=paqbrc・・・、であるときにも拡張するには、やはり、このφ(n)、「オイラー関数」が、「乗法的関数」であることを証明しなければならないのだが、それは、うまく説明できないので(笑)、省略して、そうであることにして、
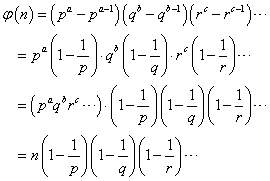
これが、「オイラー関数」であった。
- nを構成する素因数が、たった3つまでくらいなら「包除原理」、で、証明できる。つまり、
n(A∪B)=n(A)+n(B)-n(A∩B)
n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)-n(A∩B∩C)
集合「AまたはBまたはC」の要素の個数(カーディナル数)、を知りたければ、
まず、Aの個数、Bの個数、Cの個数、を足す、
でも、それでは、「AかつB」、「BかつC」、「CかつA」、をそれぞれ二度ずつ重複して数えているから、重複分を一度ずつ引かねばならない、
そうすると、今度は、引きすぎ、で、「AかつBかつC」の部分がなくなってしまうから、足し戻す、
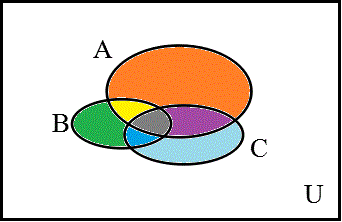
全体集合U={n以下の自然数}、
集合A={x|x∈U、xはpを因数にもつ}、
集合B={x|x∈U、xはqを因数にもつ}、
集合C={x|x∈U、xはrを因数にもつ}、
とすれば、
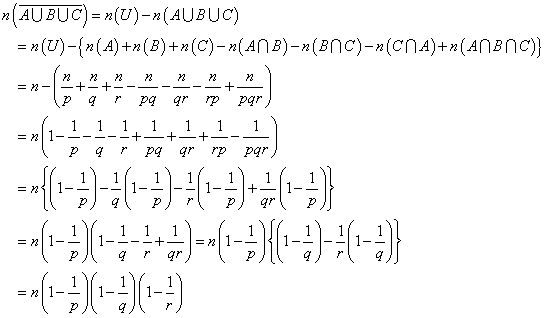
「180以下の自然数で、180と互いに素である自然数の個数を求めよ。」
などと言う、「入試問題」があったとする。180=223251であるから、「オイラー関数」によって、
φ(180)=180(1-1/2)(1-1/3)(1-1/5)=6(2-1)(3-1)(5-1)=6・1・2・4=48
とする、「小賢しい」(笑)子供の答案を、採点者が「喜ぶ」かどうか、は知らない。
むろん「包除原理」で導いてよい。
全体集合U={180以下の自然数}、
集合A={x|x∈U、xは2を因数にもつ}、
集合B={x|x∈U、xは3を因数にもつ}、
集合C={x|x∈U、xは5を因数にもつ}、
とすれば、
n(A)=180/2=90・・・2の倍数の個数
n(B)=180/3=60・・・3の倍数の個数
n(C)=180/5=36・・・5の倍数の個数
n(A∩B)=180/6=30・・・2と3の公倍数の個数、すなわち、6の倍数の個数
n(B∩C)=180/15=12・・・3と5の公倍数の個数、すなわち、15の倍数の個数
n(C∩A)=180/10=18・・・5と2の公倍数の個数、すなわち、10の倍数の個数
n(A∩B∩C)=180/30=6・・・2と3と5の公倍数の個数、すなわち、30の倍数の個数
であるから、
180-(90+60+36-30-12-18+6)=48
ここまでくれば、では、
- 自然数nと、互いに素な、n以下の自然数の和、τ(n)、
は、どう計算されるのであろうか?、が、当然疑問になるであろう。次のような定理があるそうなのである。
3以上の自然数nに対して、それと互いに素なn以下の自然数の個数φ(n)は偶数であり、
その和、τ(n)は、

とあらわされる。
この式は、n=2のときも、成立する。
「証明」は、同書には、省略されていたのだが、恐る恐るやってみて、できた、と思われるから、嬉しくなって、こんなものを書いているのである(笑)。
n≧3に対して、nと互いに素な、n以下の自然数の一つをmjとする。
(mj,n)=1ならば、(n-mj,n)=1も成り立つ。
これは、「mjとnが互いに素なら、n-mjとnとも、また、互いに素であろう」ということの表記法である。
1≦mj<nに対して、1≦n-mj<n、であり、これらは、一対一対応をなし、かつ、すべてを尽くしている。よって、その個数φ(n)は偶数でなければならず、また、その和は、次のように書ける。
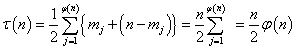
n=2のときは、2と互いに素な2以下の自然数は1しかなく、その和もまた1である。
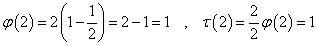
なるほど、成立している。
自然数nと互いに素なn以下の自然数の個数、オイラー関数φ(n)、および、その合計、τ(n)、を算出するプログラムを作ってみた。別に作らなければならない理由があった訳ではない。昼間が珍しく快晴であったが、そんな日に限って陽が落ちると急速に気温が下がる。暖を求めて腹や胸の上で丸くなる猫たちの重みにうなされ、何か「重い!」とか、「ああ、生きてるのがめんどくさい(笑)」とか、以外のことを考えなければならなかったから、仕方ない、「ユークリッド互除法」をBasicで書くにはどうしたらよかろう?、と、天井を睨み付けながら思いめぐらせていたら、何とか起きだす気力がわいてきたのである。何度も繰り返すが、これが、「治療行為」としての「数学」、の効用であろう。

原初の自然数「1」、は、それ自身素数ではないのだが、また、あらゆる自然数に対して、「互いに素」である。
「1」が素数でないのは、素因数分解の「一意性」を保つ「ため」の、技巧だ。
あらゆる整数が「1」と「互いに素」なのは、その定義「1以外の公約数をもたない」からの当然の帰結、と言えよう。
でも、これはちょっと悩ましい事態で、このプログラムでも、そこは誤魔化してある。互除法の演算を繰り返して、あまりが「0」になったら、それは公約数がある、ということだから、ループを出ろ!、と命ずるのだが、除数がほかならぬ「1」ならば、ちゃんと割り切れるから、「1」を「互いに素」なものとしてカウントせよ!、と機械に注文するのには、ちょっと工夫がいることになってしまう。
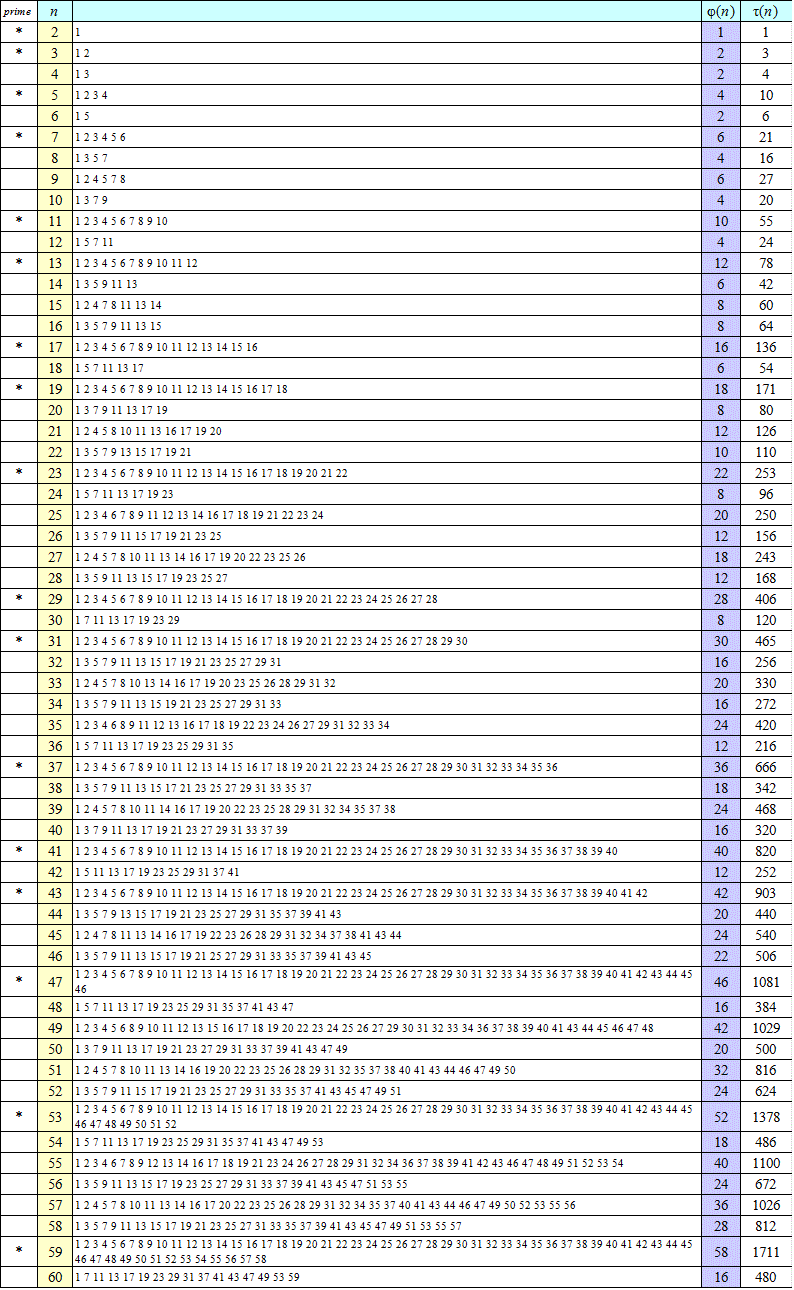
これをちょいと改良して、1から180までの自然数について、φ(n)、と、τ(n)、を計算するだけなら、「公式」があるのだから全然有難味がない(笑)ので、各nと「互いに素」なものを全部列挙してみた。
特に何も「感動」すべきところのない数表であるが(笑)、もし、nが「素数」であるならば、当然、n未満のすべての自然数は、nと「互いに素」である。したがって、そのような場合、オイラー関数φ(n)は、
φ(n)=n-1
となる。下表の最左欄「prime」として「*」をつけたのは、「素数」の意味である。これは、「素数」であるか否か?、を判定したのではなく、ただ、計算されたオイラー関数に対して、上の式が成り立っているものに、チェックを入れよ、とExcelではなくKin●softSpreadSheetに命じただけである。
で、気になった。「気になる」ことがある限り、人は「生きて」いけるのだから、ありがたいことだと言わねばならない。「生きて」いることが、「ありがたい」、限りにおいて、ではあるが(笑)。
「双条件法」と、論理学では言うのだそうだが、AならばB、かつ、BならばA、が成り立つとき、AはBであるための、同時に、BはAであるための、「必要十分条件」である、という。
nが素数であるための必要十分条件は、オイラー関数φ(n)が、以下の式を満たすことである。
φ(n)=n-1
nが素数であるならば、この式が満たされることは、上で示した。では、「逆」はどうか?
φ(n)=n-1を満たす自然数nは、か・な・ら・ず・、素数である、
と言えるのか?
「素数」は、その定義上、「1とそれ自身以外に約数をも・た・な・い・自然数」である。このように、命題の結論部分が「否定文」で書かれているとき、これは、「いかなる○○に対しても、△△となることは、決して、あり得ない」ことを示さなければならなくなるから、いわゆる「悪魔の証明」になる。
あなたの「アリバイ」を立証してください。
あなたが、当該時刻、当該場所に、「いなかった」ことを立証してください。
弁護人:指紋が残っていな・い・でしょ?、検察官:いや、それは被告人が拭き取ったのである、
弁護人:監視カメラに映像が映ってな・い・でしょ?、検察官:いや、それは被告人がカメラの死角にいたのである、
弁護人:目撃証人がい・な・い・でしょ?、検察官:いや、それはたまたま、誰も通りかからなかったのである、
こうして、ことごとく「否定文」である弁論は、ことごとく「肯定文」によって棄却されてしまうのである。「アリバイ」は、したがって、「不在」を証明していない。どこか別の場所に「存在」していた、ことをもって、「否定文」を「肯定文」に転換した「代理」の命題を論証することで、「悪魔の証明」を回避する技法なのである。
何者かが「素数」で「ある」ことの証明は、したがって、その否定文を肯定文に転換する、「背理法」または「対偶」以外の方法が、あ・り・得・な・い・。
「背理法」:φ(n)=n-1を満たす自然数であって、素数でな・い・もの、すなわち合成数nは、存在しえない。
- 単純な場合から考えよう。nがただ一つの素因数の「べき」であったとき、すなわち、
n=pa
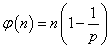
であるから、これが、φ(n)=n-1をみたすのだから、
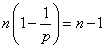
すなわち、
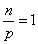
すなわち、
n=p
なるほど、a=1のとき、つまりn自体が素数のときしか、あり得ないことがわかった。
- nが二つの素因数の「べき」であったとき、すなわち、
n=paqb
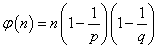
これが、φ(n)=n-1をみたすから、
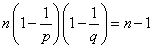
すなわち、
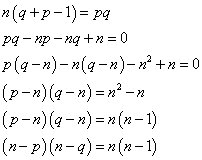
・・・
と、とんとん拍子(笑)、で進んで、ならば、その着想から、数学的帰納法めいたものを用いれば、何とかなるだろう、と踏んでいたのだが、ここで頓挫、またしても、「オチ」のない話、でも、もう十分喋ったので、ここまでにする。



また、猫たちの「重み」に耐えながら微睡んで(まどろんで)いたら、「頓挫」していた証明、思いついた、かもしれない。
「背理法」:φ(n)=n-1を満たす自然数であって、素数でな・い・もの、すなわち合成数nは、存在しえない。
φ(n)=n-1を満たすnが、合成数であると仮定すると、矛盾に導かれる。
- nが二つの素因数の「べき」であったとき、すなわち、
n=paqb
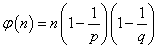
の形式ではなく、そのもとの形、
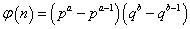
から出発すべきであったかもしれない。これが、n-1に等しいのだから、

自然数、p,q,a,bに対して、この式が満たされる、というのなら、それは、
pa-1=qb-1=p+q-1=1
が同時に成立しなければならない。
- pa-1=1から、p=1または、a=1、pは素数だから、p≠1、したがって、a=1
- qb-1=1から、q=1または、b=1、qは素数だから、q≠1、したがって、b=1
- p+q-1=1すなわち、p+q=2、このような自然数p,qは、p=q=1のみであるが、これは、p,qが素数であることに反する、
と、ちゃんと「矛盾」が帰結した。したがって、
nが二つの素因数の「べき」であったとき、
に関しては、
φ(n)=n-1
をが成立するならば、nは素数である、と断定できる。
- 素因数が三つになると、
n=paqbrc
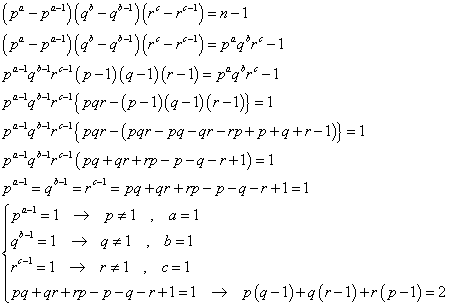
ほとんど同じ議論をして、ここまでたどり着く。一番下の式では、
p,q,rが素数であることから、
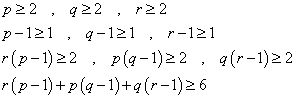
となって、やはり「矛盾」を帰結する。
- 調子に乗って、「一般化」する。nが、m個の素因数をもっている、としたら、
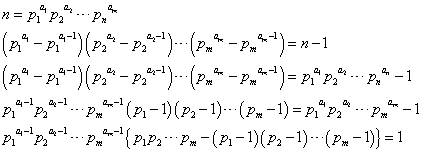
ほぼ同様の議論で、やはり最後の式の、左辺の中カッコの中身が、やはり1でなければならない、というところが「落としどころ」になるのであろう。
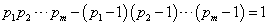
第1項は、ことごとく異なるm個の素数の積であり、第2項は、それらから1ずつ引いたものの積である。第1項の方が大きいに決まっているだろ?、しかも、その差がたった1、なんてありえないだろ?
ということを、もう少し「精緻」に、「エレガント」にかたればよいのだと思う。
もう「飽きた」から(笑)、ここまでにする。