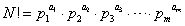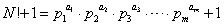もう一つの「宿題」は、何でも「フェルマー予想」というのがあるそうで、
N!+1型の素数は、無数に存在する、
ということで、この「予想」はすでに正しいことが証明されている、ユークリッドが「素数が無限に存在すること」の証明に用いたような「初等的」な方法でも、証明できる、とのことであって、
へぇっ？、そんなの簡単じゃん、
と、ばかりに、「オイラー関数」などで、このところ「素数」づいていた私は、調子に乗って、無謀にも、考えてみることにした。

ユークリッドによる、素数の無数性、の証明は、今日の言葉に書き直せば、こんな感じなのだ、と言われている。
「無限に存在する」、すなわち、「その個数には、限りが、な・い・」、これは「否定文」であるから、やはり「悪魔の証明」であり、「背理法」または「対偶」という、否定文の肯定文への転換、を要する。
背理法：「素数が有限個しか存在しない、と仮定すると、矛盾を帰結する」
素数が、m個しか存在しないとする、すなわち、素数をす・べ・て・、小さいものから順に、列挙すると、
p1,p2,p3,・・・,pm
であった、と仮定する。「列挙」できる、ということが、「有限」であることに対応している。
これらの素数をすべてかけて、そこに1を加えた数を考える、すなわち、
N=p1×p2×p3×・・・×pm+1
この数は、
p1で割ると、あまりが1である、
p2で割ると、あまりが1である、
p3で割ると、あまりが1である、
・・・
pmで割ると、あまりが1である、
から、
p1,p2,p3,・・・,pm
のいずれとも、互いに素、であることになる。
ところでこの数は、明らかに、最・大・の・素数pmより、大きい。
最・大・の・素数pmより、大きく、かつ、すべての素数と互いに素なのだから、これは、新・た・な・素数である、と言わねばならない。
ならばこれを、pm+1と名付け、・・・、としても、同じ操作により、また一つ、新・た・な・素数が、生み出されてしまう。
つ・ね・に・、1を付け加えることができる、ことが、「無限」を生成する。
こうして「有限」から「無限」が生み出された、「最大のもの」より、つねに「それより大きなもの」が存在することがわかった。これは「矛盾」である。Q.E.D.

「証明終わり」、として、Q.E.D.などと書かれることがあって、大方ラテン語の頭文字なのだろ？、いつか調べようと思っていたが、「老い先」が短くなってくると、そんな風に引き延ばしていたら、「知らずに死んでしまうかもしれない」(笑)と「不安」になって、いや、人間の「記憶」は、呼吸と代謝に支えられた「揮発性メモリ」なのだから、「死んだら」、「知っていて」も、同じなんだよ、とは言うものの、時間を持て余したご隠居であることだし、手元には、「Exceed英和／和英辞典」、「広辞苑」、「新字源」が常備されている。
QED:quantum_electrodynamics、「量子論的電子動力学」？、いえいえ、
QED:quod_erat_demonstrandum、前にも「薀蓄（うんちく)」を披露した通り、ラテン系諸語の疑問詞、関係詞はquで始まることが多い。だから、quodは「what」だろう。eratは「be動詞」だろうな。だったら、
(This_is)_what_is_to_be_demonstrated.「これが、示さるべき事柄であった」、
みたいな感じか？

では、「フェルマー予想」。
自然数Nに対して、N以下の素数がm個あり、これを小さいものから順に列挙すると、
p1,p2,p3,・・・,pm
であったとする。すると、N!は、N以下の自然数の積なのだから、その素因数は、これらm個の素数に限られる。すなわち、

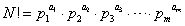
ならば、

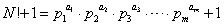
であるから、この数は、p1,p2,p3,・・・,pmのいずれとも互いに素である。

と、ここまで書いて、頓挫したことがわかった。これは、上のユークリッドの素数の無数性、の証明の焼き直しであって、これも同じく、
「もし」、素数がこのm個しか存在しないんだとしたら、N!+1は、
最大の素数pmより大きく、かつ、
p1,p2,p3,・・・,pmのいずれとも互いに素、
であるから新たな素数であり、「矛盾」、と、素数の無数性の証明の「背理法」の結論部分に使えるにすぎなく、
N!+1自体が、素数であるとも、また、その形の素数が無数であるとも、少しも言えそうにない。
N!+1が、pmより大きいいくつかの素数のみによる合成数である可能性を否定できないからだ。
現に、
4!+1=25=52
5!+1=121=112
ではないか！

で、あきらめて(笑)、また機械の力に頼ることにした。
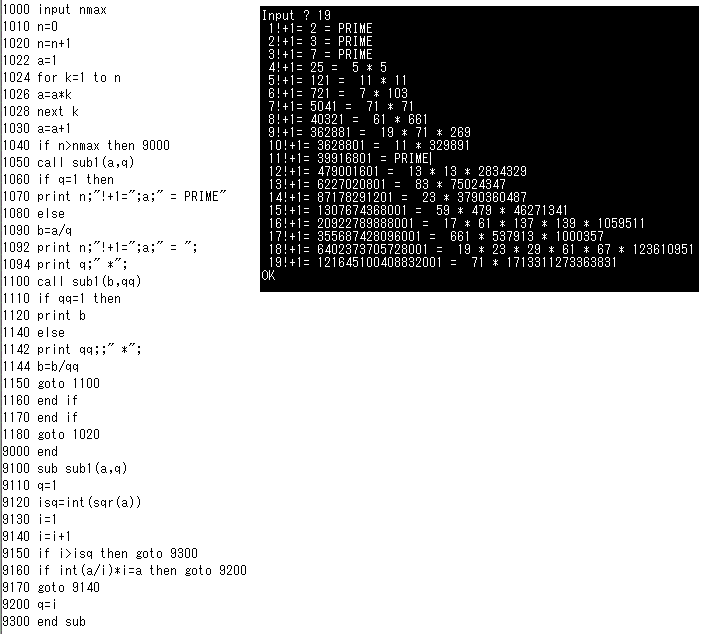
N!+1を、N=1,2,3,・・・、と順次計算して、素数かどうか判定する、素数でなければ素因数分解する。N=19あたりが精度の限界のようで、そこまでのところでは、どうやら、素数よりも、合成数の方が「多数派」らしいのである。やや、意外、の感に打たれる。お手元のパーソナル・コンピュータでは、ここまでしか調べられないのだから、一体フェルマー氏は、紙とペンを使って、どうやってそんな途方もない「予想」ができたのだろうね？
それにしても、例えば、7!+1=712など、ほとんど「魔術的」というべきではないか？、「自然数」、「カーディナル数」の「深淵」を見る思いである。
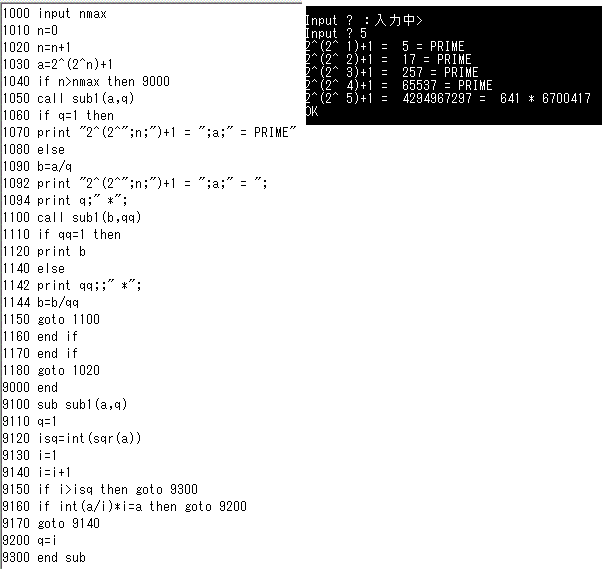
どうも、「フェルマー素数」、というのは、Fn=22nという形のものであるらしい。フェルマーは、これがすべて素数になる、と予想した。 とのことだ。上で用いたプログラムをちょいと改変して、計算すると、早速F5が既に合成数であることがわかる。そして、パーソナルコンピュータの精度では、ここまでしか計算できないことも、同時に、わかった。17世紀に生きたフェルマー氏を、5くらいまで計算してみなかったのか？、と責めるのは不当であると言えるだろう。

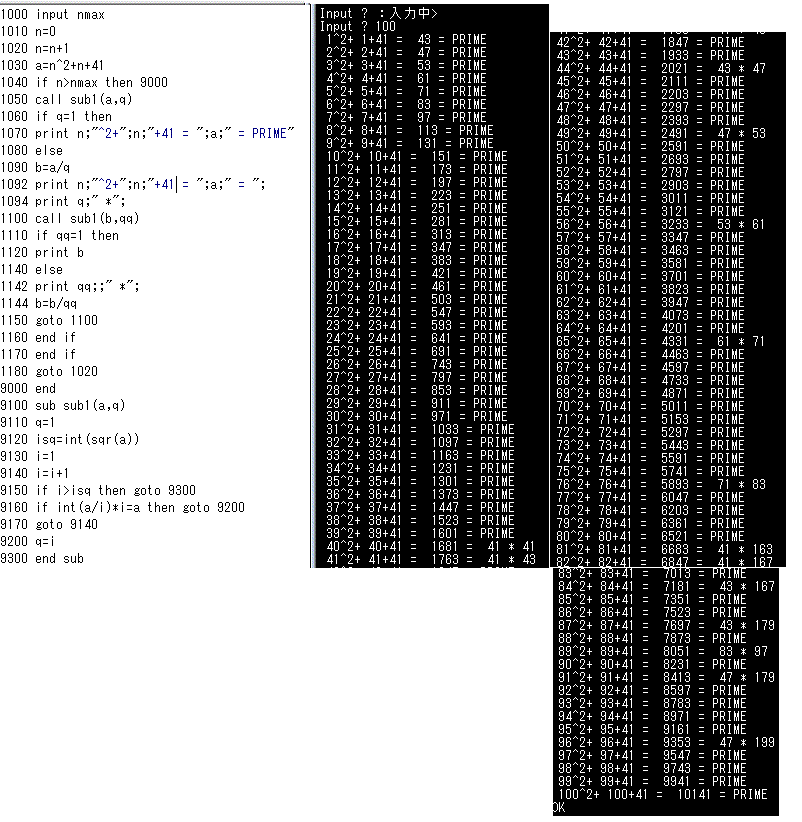
この「フェルマー素数」のF5が素数でないことを初めて示したのが、18世紀のオイラーなのだそうだ。オイラーは、こんな式をも、提案している。「オイラーの、素数生成多項式」と呼ばれる。
x2+x+41
x=41のとき、41を因数にもつ合成数になるべきことは、「容易に」(笑)想像がつくが、そのほぼ直前のx=39までがことごとく素数であるのは、なかなか不気味である。
さらに、x=40のとき、
402+40+41
=402+40+(40+1)
=402+2×40++12
=(40+1)2=412
などというのも、神秘的、というのか、魔術的、というのか、やはり、ちょっと、気持ち悪い。
これもプログラムを改変するのは簡単だから、やってみた。今度は、数はそう大きくならないから、100くらいまでは、問題ない。ただ、徐々に合成数の割合が増えてきて、「神秘性」は、薄れてくるが(笑)。