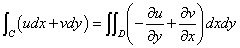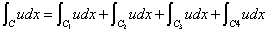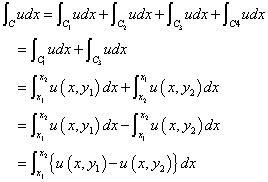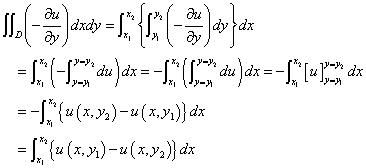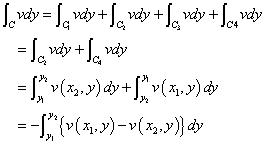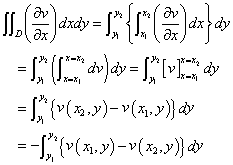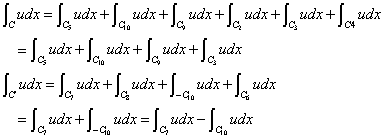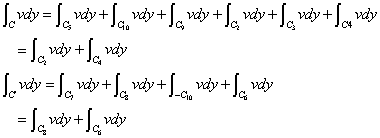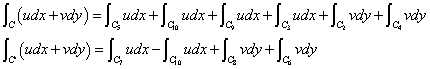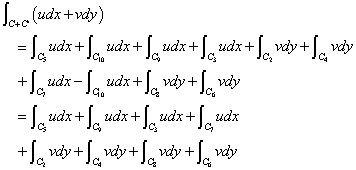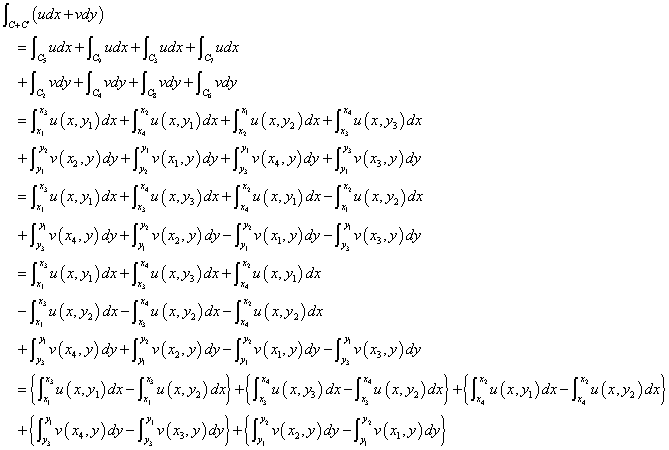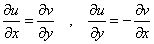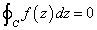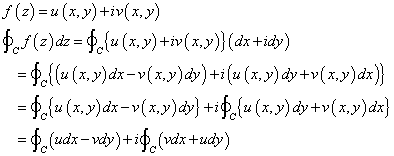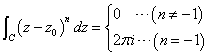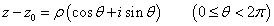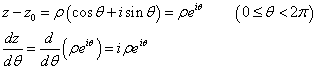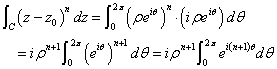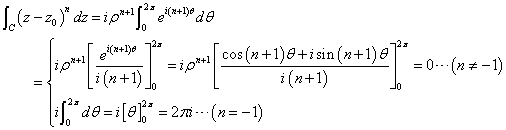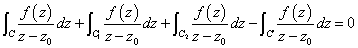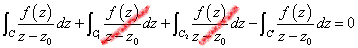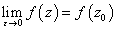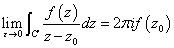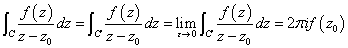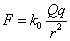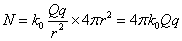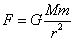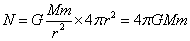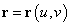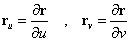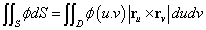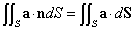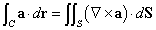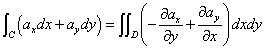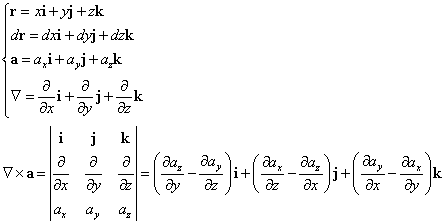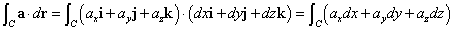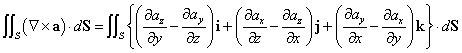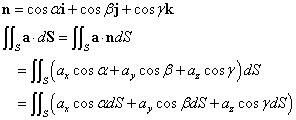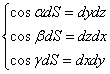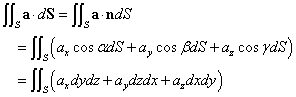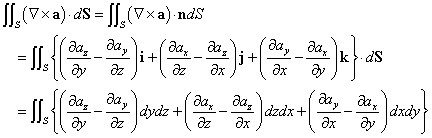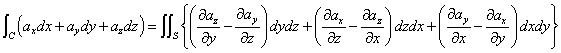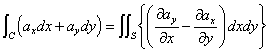空間内の領域D、「ドメインdomain」というのは「定義域」のことだったのだ!、の各点P(x,y,z)において、実数(スカラー)φが定義されるとき、この
φ(x,y,z)
を、「スカラー場φ」と呼ぶ。同様に、
Dの各点P(x,y,z)において、ベクトルaが定義されるとき、この
a(x,y,z)
を、「ベクトル場a」と呼ぶ。
- スカラー場φに対して、
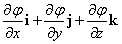
で表されるベクトルを、φの「勾配」と呼び、gradφ、または∇φと書く。すなわち、
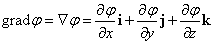
ここに、i,j,kは、それぞれ、x方向、y方向、z方向の、単位ベクトルである。
ここに定義されたような「演算」、「作用」をφに施すことをもって、∇φと、あ・た・か・も・、掛け算であるかのごとき表記をすることの連想から、φを取り去った、空っぽの∇、∇のうしろに「ゼロ記号」が隠されている、と言ってもいい、を、「ハミルトン演算子」、「ハミルトンの作用素」などと呼ぶ。すなわち、
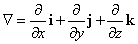
ちなみに、記号∇は、「ナブラnabla」と呼ばれる。その形に似た「竪琴」のギリシャ語名に由来するとのことだ。また、gradは、gradient、勾配、変化率、の略。
- ベクトル場aに対して、この「ハミルトン演算子」を、左から作用させるには、ベクトルとベクトルの「掛け算」に、「内積(スカラー積)」と「外積(ベクトル積)」の二様があることに対応して、以下の二つが定義される。
- ∇・aを、aの「発散」と呼び、divaと書く。
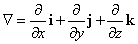
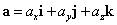
に対して、
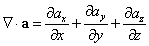
divは、divergence、分岐、発散、の略。
- ∇×aを、aの「回転」と呼び、rotaと書く。
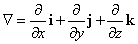
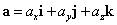
に対して、
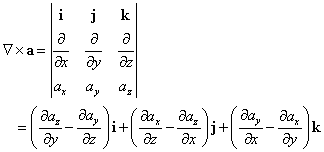
rotは、rotation、回転、交代、の略。curlとする記法もある。
上で用いた「内積」と「外積」の計算方法について、まとめておく。

a、bのなす角θ、に対して、
- 内積a・bは、
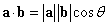
であるから、それぞれ直交する単位ベクトルi,j,kに対しては、
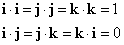
したがって、
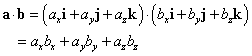
- 外積a×bは、

ここに、nは、ベクトルaをベクトルbに重なるように、最小の角度(π以下の角度)で回転させるとき、それを「右ねじ」の回転に見立て、その進行方向の単位ベクトル、とする。
したがって、「外積」には交換法則が成り立たない。
それぞれ直交する単位ベクトルi,j,kに対しては、
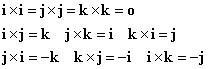
したがって、
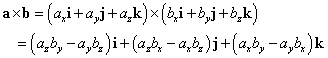
3次の正方行列の行列式の計算方法との類似性から、次のように表記することもある。すなわち、
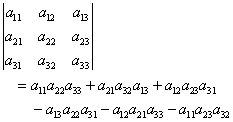
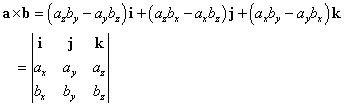
では、まず、「勾配」∇φ、の、意味、の説明を試みる。
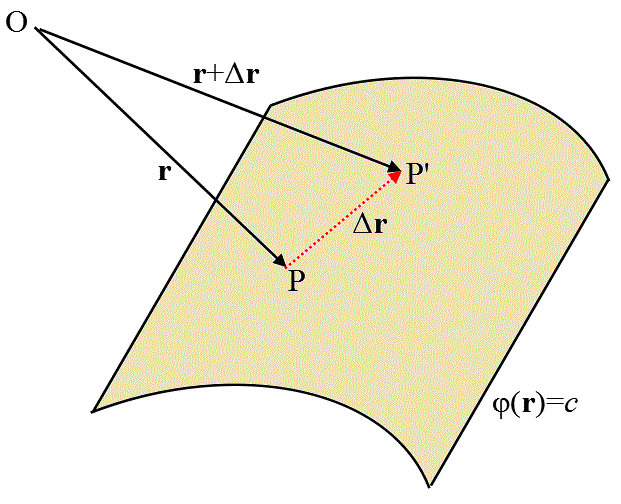
空間内の動点あらわす位置ベクトルr、および、定数cに対して、
φ(r)=c
は、ある曲面を表すであろう。これを、スカラー場φの「等位面」と称す。その曲面上のどの点でも、φは、等しい値cをとるからだ。
cを変数とみれば、この式は、そのそれぞれの値に対して、様々な曲面を表すことになるから、「cを媒介変数とする、曲面族」と呼ぶ。
「等位面上」では、φは同じ値をとるから、dφ=0である。
これを、いわゆる(笑)、「全微分表示」すると、どういう場合にそんなことが許されるのか?、私は説明できないが(笑)、
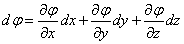
であるから、
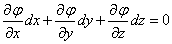 ・・・(1)
・・・(1)
一方、
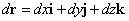 ・・・(2)
・・・(2)
ここで、
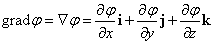 ・・・(3)
・・・(3)
であったことを思い出せば、(1)式は、(2)と(3)の「内積」がゼロだ、と言っていることがわかる。すなわち、
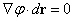
二つのベクトルの「内積」がゼロだ、ということは、そのなす角の余弦(cos)が0、ということだから、この二つのベクトルは、互いに垂直であることになる。
ところで、上の図に見るように、dr、ないし、Δr、というベクトルは、この曲面上の任意の点Pをごくわずか移動させた点をP'とするとき、PP'を結ぶベクトルを表す。その長さが十分小さければ、近似的には、点Pにおけるこの曲面の「接平面」上のベクトルと言える。
また、P'は、Pの近傍ならばどこにとってもよかったはずだから、dr、ないし、Δrは、「接平面」上の任意のベクトル、ということになろう。
一般に、ある平面に含まれる任意の直線と、垂直な直線は、その平面と、垂直である、と言われる。
平面上の任意のベクトルは、ただ2個の「1次独立(線形独立)」なベクトル、これを「基底」という、の「1次結合(線形結合)」で表現できるから、究極的には、たった二つの相互に独立なベクトルと垂直であれば、平面そのものと垂直であると言えるのであるが、・・・。
つまり、ここで分かったことは、「勾配」∇φは、曲面φ(r)=c上の、任意の点rにおけるその接平面と、垂直である。
曲線上のある点での接線と、その接点において直交する直線を「法線」と呼ぶ如く、曲面上のある点での接平面と、その点において直交する直線もまた、「法線」と呼ばれる。
つまり、「勾配」∇φは、曲面φ(r)=c上の各点における、「法ベクトル」を表している!
これが、「勾配」の、一つの「意味」であるようで、他にも諸々のものがあるのであろうが、うまく説明できそうなのは、これくらいだったので、勘弁願おう。
物理学的な具体例として、「万有引力による位置エネルギー(ポテンシャル)」というスカラー量と、「万有引力」そのもの、というベクトル量の関係、についてお話ししたいが、若干の準備がいるので、それは、次回に、・・・。
「場」という言葉は、しかし、少々すわりが悪い、と思う。あるいは、私が単に「バッタもん」の物理講師だ・っ・た・、から慣れていない、に過ぎないのかも知れないが、それも、済んだ話(笑)、だ。
空間内の一点の座標(x,y,z)を指定したとき、これにスカラー量φ(x,y,z)が「対応」するとき、その「関数」φをもって、「スカラー『場』」と称し、
同じく、ベクトル量a(x,y,z)が「対応」するとき、その「関数」aをもって、「ベクトル『場』」と称するのである。
元来、物理学用語であったものが、ベクトル解析、などの数学の分野にも「流用」されたものであるらしい。英語では、「スカラー場scalar_field」、「ベクトル場vector_field」、のようだから、これは、「磁場magnetic_field」などと同じ用法である。遠山啓「現代数学入門」(ちくま学芸文庫)に載っていたが、数学上の「群・環・体」のうちの「体」は、ドイツ語ではKorper、文字通り「身体」であるが、英語では、その語に対応するcorpusが「死体」を連想させるので嫌われ、fieldと呼ぶのだそうであるから、混乱が生ずる余地がある。
ちなみに「スカラー」は「学者scholar」(笑)ではなく、scalar、「スケール」scaleは、動詞なら「大きさを測る、計量する」であるから、「計量できるもの、計量すべきもの」みたいな由来なのであろう。綴り字に忠実であれば、英語なら「すけいらー」と発音すべきなのだろう?、知らないけど(笑)。さらに「薀蓄」としては(笑)、「学者scholar」の方は、ドイツ語由来なんだろう。sch「エス・ツェー・ハー」という綴り字は、3文字セットで一つの子音扱いで、「しゅ」みたいな音になる。英語を習いたての中学一年生は、「学校school」などというものを「基本単語」として覚えなければならず、ところがこれが、英語のつづり字―発音の対応ルールの上では、かなり例外に属するものであるので、まったく支離滅裂なものとしか思えず、挫折する(笑)、という次第である。
高校の物理で取り上げられる「場」の理論は、ただ二つ、「電場」と「磁場」。
「電場」は、次のように定義される。
単位正電荷、+1Cの電気量を帯びた、「大きさのない」もの、を、「そこ」に置きたまえ。すると、その「もの」に「力(静電気力)」が生じたとしたら、その「力」をもって、その「場所」、ほかならぬ「そこ」の「電場」とする。
「力」は、大きさのみならず方向を要素とする「ベクトル量」であるから、これは、「そこ」という「場所」を指定することによって、一つの「ベクトル量」が得られたのだから、まさに「ベクトル場」である。
「磁場」は、もっと悩ましい。磁石というものは、どんなに小さく叩き割っても、決してN極とS極を分離することがかなわず、つねに一つの磁石の中にN極とS極が相補的に存在してしまうから、「単位N磁・荷・」などというものがあり得ないからだ。だから、「電場」とパラレルな形で「磁場」を定義することができず、高校の教科書でも、そこは「言葉を濁している」はずだ。
正確な定義は、これは、山本義隆氏、20代の「若気の至り」かも知れないものを、こんな風に繰り返し引用するのはあるいは失礼だろうが、敬愛の念、ということで寛恕願うことにして、元「東大全共闘」の、「自己否定に自己否定をかさね、最後には単なる一物理学ととなって、・・・」の山本義隆氏、の手になる、極めて優れた、駿台予備学校の物理教科書で知ったのだが、
「磁場」の定義には、もう少し「迂回路」が必要で、さしあたりは、「磁場」なるものが存在するとして議論を進め、「ローレンツ力」を導入したのち、
速度vで運・動・す・る・、電気量qの荷電粒子に、ローレンツ力F=Bqvを生じるような「空間」を、
その大きさが、磁束密度Bで与えられ、
その向きが、「フレミングの左手の法則」によって決定される、
「磁場」としよう、ということであるらしい。
「ベクトル場」としての「万有引力」、「スカラー場」としての「万有引力による位置エネルギー」、に話を進めたかったのだが、余分な話をして、既に飽きてきたので、本日はここまで。
さて、「万有引力」であるが、
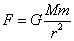
質量がそれぞれMとmである二つの物体が、距離rを隔てて存在しているとき、両者の間には、比例定数をGとして、上の式であらわされる如き「引力」が作用する。
距離の2乗に反比例するわけで、「逆二乗法則」とも呼ばれる。「世界」には「逆二乗法則」に支配される現象が、多々あるので、それはほとんど「神秘的」ともいうべきなのだが、もちろん、きっと「裏」がある。
「シャボン玉」を想像しよう。ストローの先に石鹸水をつけて、息を吹き込むと、「球」は見る見る大きくなる。ちなみに「シャボン」はフランス語の「石鹸(せっけん)」sabon「さぼん」なんだよ、と、得意そうに言おうと思って、念のため広●苑引いたら、ポルトガル語sabaoだって。「せっけん」は高級脂肪酸グリセリンエステルの加水分解生成物(笑)であるから、カルボン酸イオンや、カルボニル基の非共有電子対のあたりに強力な電荷の偏りがあって、強い結合力を発揮するから、なかなか割れないのだな。今、ある瞬間、この「球」の半径が、rであったとする。その表面積πr2に、「せっけん」分子は均等に、えっと、特に「均等であってはならない」理由がない限り、これを「理由欠乏の原理」と呼ぶ、配分される。息を吹き込むことによって、「球」の半径は増大し、あるとき、もとのk倍、krになったとしよう。表面積は、長さの二乗の次元をもっているから、k2倍になる。「せっけん」分子の個数は、変わっていないはずであるから、その「濃度」は、k2分の1に、薄・ま・る・。これが、「逆二乗法則」の、「裏」である。
ストローの先端から個々の「せっけん」分子に向かって、「矢印」を描いてみる。一点から発し、あらゆる方向に延びる矢印は、延びれば延びるほど、その先端同士は、離れていく。この「矢印」を「流束flux」と呼ぶ。
万有引力であるならば、質量の「源」、大きい方の(笑)Mを「湧き出し口source」として、この「矢印・流束」が発し、
静電気力に関するクーロンの法則であるならば、正電荷を「湧き出し口」として、「流束」が、この場合は、高校の物理でも学ぶ「電気力線」または「電力束」が、発している、
と、見ることになるのである。これが、平たく言えば、もちろん、「私」が、「平たく」しか言えないからだが(笑)、「ガウスの法則」、である。
万有引力は、静電気力などに比べると、非常に微弱な力で、私たちが通常目にするようなサイズの物体間に作用するところを、目撃することは、決して、できない。ほら、机の上のボールペンと消しゴムの間にも、万有引力が作用しているんだよ!、などという説明は、あまり意味をなさない(笑)。少なくとも一方が、「天体」という巨大な質量塊でない限り問題にすべきではない。ここでは、大きい方のMを「地球」とする。
私たちは、地球が「球体」であることを「知っている」はずであるが、・・・、たとえば私は、今、沖縄、という小さな「島」に住んでいて、しばしば海岸に立つことがあるから、「水平線」を見ることができる。冷静に考えれば(笑)、それが、少なくとも、地球が「平面で・は・な・い・」証拠になる。比叡山から東山、愛宕山から西山、わずかに南だけが、淀川水系の切り開く平野になっている、「京都盆地」に住んでいた時とは、えらい違いなのだな、・・・、その「球体」の半径は、あまりにも大きすぎて、私たちの想像を絶するから、万有引力が地球の重心、すなわち中心に向う、と言われたって、それは、つねに私たちの足元、「下の方」を向いている訳で、さらに、私たちが住んでいる世界は、高さ方向では、地球表面のごく限られたエリアだから、「ミクロ的」には、
「重力」は、いつも、「下」に向かっていて、
その大きさも、地球の半径をRとすれば、

なる一定値を示すことになる。g=GM/R2を、「重力加速度」と呼ぶ。
その、単純な方の「ミクロ」世界、から始めると、左図であるが、
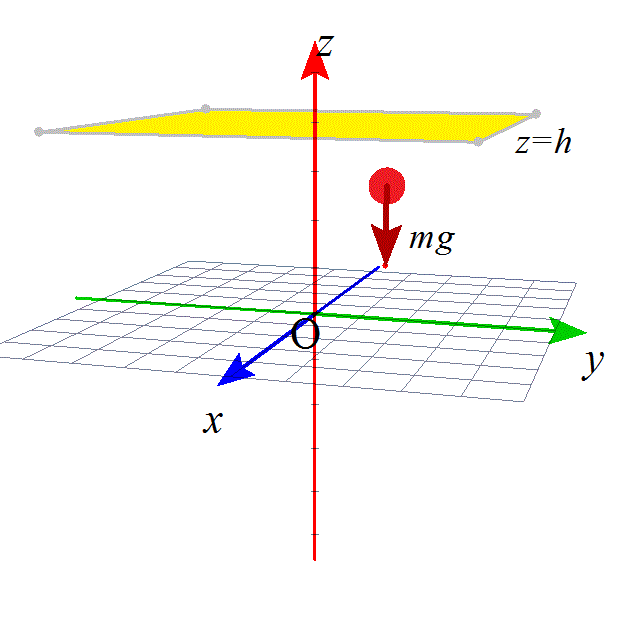
「重力」による「位置エネルギー」は、次のように定義する。
ある基準面を定め、そこから、問題にしたい場所まで、質量mの物体を、「重力」とちょうど釣り合う力によって、運んだとき、要する仕事。
ちょっと待て、「ちょうど釣り合った力」なら、運べないだろう?、という笑い話は、実は物理学上の「難問」で、だから、微小時間内では釣り合いを保ちながら、「じわじわと」、「準静的に」動かす、などと言いぬける。
地表面をxy平面、「上」、「空(そら)」に向かってz軸をとる。質量mの物体には、つねに、z軸負方向に一定の大きさmgなる「重力」、方向も加味して、-mgが作用する。これとちょうど釣り合う力は、「上」向き、z軸正方向のmgであるから、
地表面z=0を「基準面」とし、z=hという「場所」の、「重力」による「位置エネルギー」Uは、
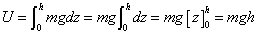
となる。地表面上のどこでもよかったから、x、yを任意として、(x,y,h)なる「場所」を指定すると、mghなる「値」が得られたわけである。「仕事」は、「『力』と、その作用方向への『移動距離』の積」、または、「『移動距離』と、その方向への『力』の成分の積」」、であるから、まさに、ベクトル量「力」と、ベクトル量「移動距離」の「内積」であって、したがって、スカラー量である。
「場所」を指定すると、「スカラー量」Uが得られたのだから、これは「スカラー場」である。
さて、
「勾配」∇φは、曲面φ(r)=c上の各点における、「法ベクトル」を表している!
のであった。スカラー場Uに対して、∇Uを計算する。
一般的な「場所」、(x,y,z)に対して、U=mgzであるから、
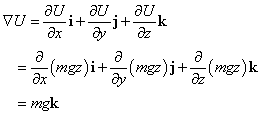
平たく言うと(笑)、積分したものを微分したんだから、当たり前。なのだが、確かに、これは、「重力」、-mgの反対向き、のベクトルで、なるほど、
U=mghなる、スカラー場Uの「等位面」z=hに垂直、つまり「法ベクトル」である。
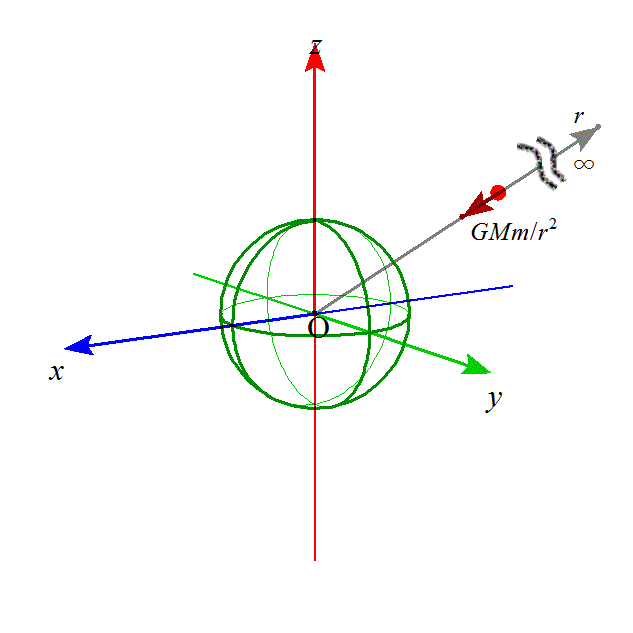
「マクロ」世界、の右図に移る。
「逆二乗法則」では、距離0で「力」が∞、になってしまうから、「第一種の異常積分」を生じ、困ってしまうから、「力」が0になってしまう「無限遠点」を「基準面」に採用する。今度は「第二種の異常積分」なのであるが、今からやってみるように、収束するから、いいのだ(笑)。
上と同様、「定義」に従って計算する。
「基準面」すなわち「無限遠点」から、問題にしたい場所、地球の中心から距離rの地点、まで、地球の中心に向う「万有引力」とちょうど釣り合う力、すなわち、地球の中心から「外向き」の、GMm/R2を、「じわじわ」加え続けて運ぶ時に要する仕事、
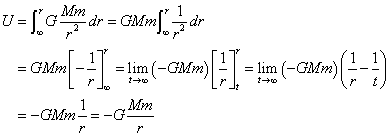
同様に、
「勾配」∇Uが、その「等位面」、これは、半径rの球面である、の「法ベクトル」であることを、確認したい。
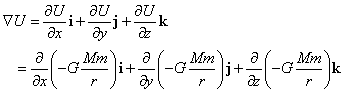
ここで、
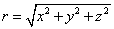
であるから、
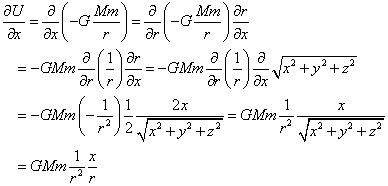
同様に、
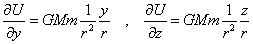
したがって、

ところで、右辺のかっこの中身は、r=(x,y,z)方向の単位ベクトル、r/rに他ならない。すなわち、
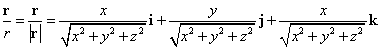
であるから、
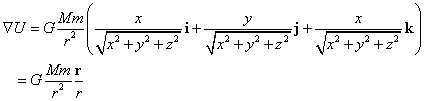
なるほど、これまた、万有引力そのものの、反対向きの力のベクトル、中心から「外」に向かうから、当然、球面たるUの「等位面」とは、垂直、なのであった!
次は、「発散」∇・aの意味について。「流体」の中に、下図のような、仮想的な直方体、各辺の長さが、それぞれΔx、Δy、Δz、であるようなものを考える。
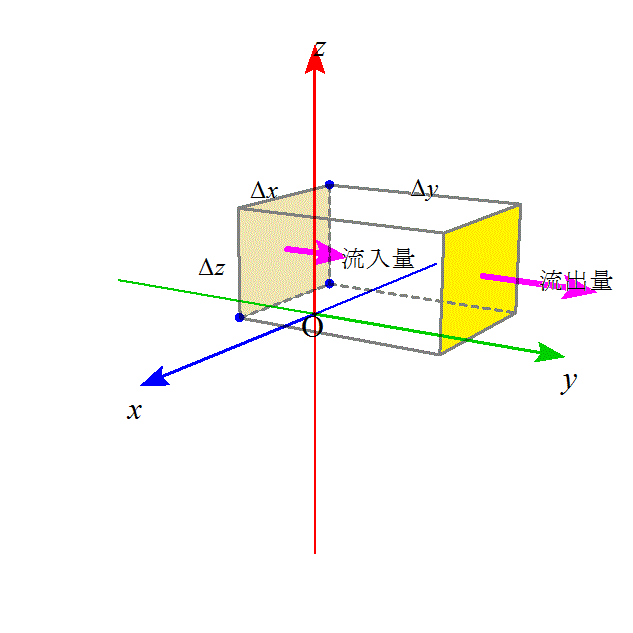
この流体内部のいたるところ、その「密度」も、流れの「速度」も、場所ごとにことごとく異なっている可能性がある。
つまり、「密度」ρは、場所(x,y,z)の関数である。「密度」は大きさのみをもち、方向をもたない「スカラー量」であるから、これは、「スカラー場」ρ(x,y,z)、と言える。
「速度」vは、やはり場所(x,y,z)の関数である。「速度」はベクトル量であるから、「ベクトル場」vであって、
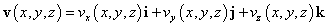
と、書くことができる。
のちに用いることになるので、用意しておくが、「スカラー量」ρと「ベクトル量」vの積ρvは、「ベクトルのスカラー倍」すなわち「ベクトル量」であるから、これまた「ベクトル場」ρvと呼んで差支えないだろう。次元としては、[kg/m3]と[m/s]の積、[kg/(m2・s)]、なる、わかりにくい量なのであるが、・・・。
では今から、図に書き込んだように、例えばy軸方向を例にとって、その座標軸の正の方向に沿って、左側の面から「流入」し、右側の面から「流出」する「もの」の「収支」を明らかにしたい。「流入/流出」する「もの」とは、なんであろうか?、「質量」なのである。密度ρ[kg/m3]に、微小な体積ΔxΔyΔz[m3]をかければ、なるほど、[kg]となるであろう。
この流体は「等方的」と考えている。つまり、例えばy軸に沿って起こった事柄は、そのまま文字をすり替えれば、x軸上でも、z軸上でも、起こっている、と考える。例えば「重力の影響」などというものを加味すると、z軸だけは、別扱い、などということになるが、ここではそうはしない、と言っている。
この直方体は微小なものなので、その一つの側面の上では、ρもvも一定であるとみなすことができる。
では、図の、y軸に垂直な、左側の面から、この直方体の内部に向かって、微小時間Δtの間に、流入する質量は?

と、書けることになろう。Δtという時間の間に、左側の面は、vyΔtという長さだけ、直方体の内部に「押し込め」られた、直方体薄片に含まれる「もの」が、流入量なのである。
では、右側の面から、同じく微小時間Δtに、流出する質量は?、今度は、Δyももちろん微小量なのであるが、今問題にしているy軸方向の流れに沿って、わずかでも距離が隔たれば、密度も速度も、変わってしまう、と考えなければ、そもそも「収支」が出てこない。だから、ρもvyも、変わるのであるが、そこは、やはりΔyは十分小さい量であるから、ということで、「1次近似」を採用する。
「1次近似」というのは、曲線を十分短い区間で眺めれば、線分とみなせるから、当該十分短い区間の中では、左端における変化率のまま1次関数として変化する、と仮定する手法である。つまり、

という訳だ。とすると、右側の面からの流出量は、
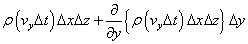
ということになろう。Δx,Δy,Δz,Δtは定数であるから、偏微分記号の外に出して、
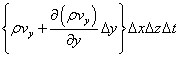
さて、では、その「収支」をとる。「流出量」をプラスとすれば、「流入量」は、負・の・「流出量」と言えるから、「流出量」から「流入量」を引き算することで、「正味の」、「流出量」が得られる。すなわち、
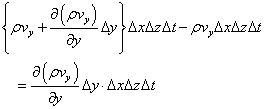
ここで、先ほどものべたように、「空間の等方性」から、他のx軸、z軸においても、同様の事態が生じていると考え、その「合計」を求めたいと思う。
この式で、vyは、速度ベ・ク・ト・ル・のy方向成分であるから、あくまで「スカラー量」であることに注意しなければならない。だから、x軸、y軸、z軸、それぞれの「流出量」を加算するには、単に「スカラー的」に、足し算することで足りる。すなわち、
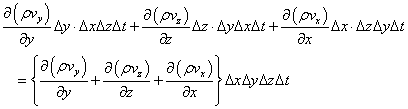
ところで、「ハミルトン演算子」∇は、
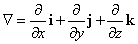
また、先ほど予告したように、ベクトル量ρvなるものを考えれば、
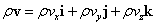
であるから、上の「正味の」流出量は、「内積」を用いて、
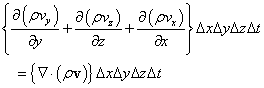
となる。これが、「発散」の意味、微小体積ΔxΔyΔzから、微小時間Δtに、流出する質量は、ベクトル量ρvΔxΔyΔzΔtの、「発散div」である。
単位体積、単位時間当たりに換算すれば、ΔxΔyΔzΔtで割って、ベクトル量ρvの「発散」が。流出量である、と言ってもいい。
ところで、もし、ここで求めた「正味の」流出量が、
- 正の値であるとしたら、それは、入って来た「もの」より、出て行った「もの」の方が多い、ということであるから、「中」にあ・っ・た・「もの」、在庫、ストック、蓄積量、は、「減った」筈であり、
- 負の値であるとしたら、それは、入って来た「もの」の方が、出て行った「もの」より多い、ということであるから、「中」にあ・っ・た・「もの」、在庫、ストック、蓄積量、は、「増えて」いなければならない、
だろう。微小時間Δtの間に、微小体積ΔxΔyΔzの「中」で、質量が「生成」するとすれば、この流体の密度が、時間的に変化することが前提であって、その「生成量」は、これまた「1次近似」として、
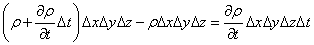
となる。「中」での「生成量」と、「中」から「外」への「正味の、流出量」の合計が、つねにゼロである、一方が正ならば、必ず、他方は負である、これが、「質量保存則」、ということになる。すなわち、
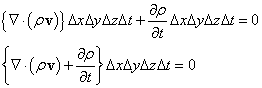
単位体積、単位時間あたりで考えれば、
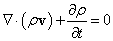
手元の「教科書」では、これらは半ページくらいの分量であっさりと説明されているのであるが、相変わらず「頭の悪い」学生である私は、これだけくどくど(笑)付け加えねば、「読み進む」ことが、できなかったのであるな。これで35年来の「宿題」(笑)の「半分」までは済んだ。残るは「回転rot」である。
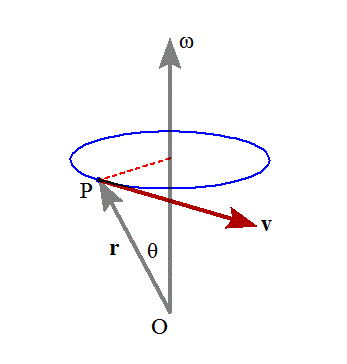
では、「回転」。流体中に「渦」ができているとする。位置ベクトルrであらわされる点Pにおける、この「渦」を構成する媒質の速度ベクトルが、vであったとする。図の上方から覗き込んで、「反時計回り」に渦巻いているのである。
高校の物理では「角速度」 は「スカラー量」として扱う。2次元平面内での等速円運動を問題にしているのに、その平面と垂直な方向に、突然矢印が突き立つのが「奇異」と思ったのだろうか?、でも、別のところでは、例えば「アンペールの法則」、電流がまわりの空間につくる磁場の方向を決めるのに、ちゃんと「右ねじの法則」を使っているのにね。
「右ねじの法則」は、回転方向を特定するのに、とても分かりやすい命名法だと思う。ドライバーをどっちに回せば、ねじが「進む」つまり「締まる」かを、大工仕事を一度でもしたことのある人なら、誰でも知っている。ペットボトルのキャップでも、ボールペンの軸でも、およそ「ねじ」が切られているもののほとんどは、「右ねじ」だ。ドアのノブだって、押して開くドアだったら、右に回して「失礼します」などとと言ってドアを押して入る。手前に引いて開くドアもあるだろうから、困るのだけれど(笑)それにしたって、「シンボリック」な意味で(笑)「開く・前に進むことができる」事態と、右回り(時計回り)に回す、という行為が結びついている。だからきっとこれは「万国共通のルール」で、では、なぜ、そうなっているのか?、と考えるに、人間の身体の「ハードウェア」的な構造からして、右手を、時計回りに回転させる方が、その反対の回転よりも、力を加えやすく、大きなモーメントが発揮できるからなんだろう、と思う。ということは、「ポリティカル・コレクトネス」を信条とする者としては、直ちに反省しなければならない、これは、「左利き」という少数者を除外している。
かつて(笑)、物理の授業をしながら、「右ねじの法則」が出てくる度に、これ、英語でどう言うんだろう?、そのうち、調べようと、そのままになって今日に至った。手元の大学の物理学の教科書などには、記述が見当たらなくて、不本意だけれども(笑)、W某ペディアに問い合わせたところ、「右ねじの法則」はこの国固有の言い方で、英語では「right-hand_rule」、だというのだが、それは「右手の法則」であって、やや意味が異なってきてしまう。
3次元空間を表示する直交座標には、
- 正四面体の四つの面を、例えば「赤、黄、青、緑」の4色を一回ずつ使って塗り分ける場合の数が、2であるように、
- 不斉炭素原子をもった化合物、例えば、乳酸H3C-C*H(OH)-COOH、には2種類の異性体が存在するように、
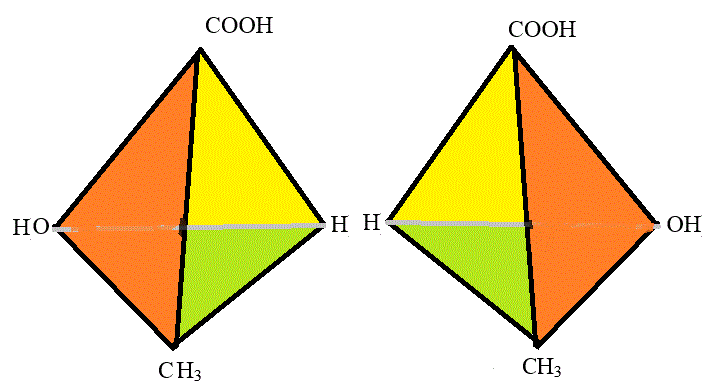
互いに「鏡像関係」に立つ二つの定め方がある。x親指、y人差し指、z中指、になぞらえたとき、それが「右手」であるものを「右手系」、「左手」になるものを「左手系」と称す。
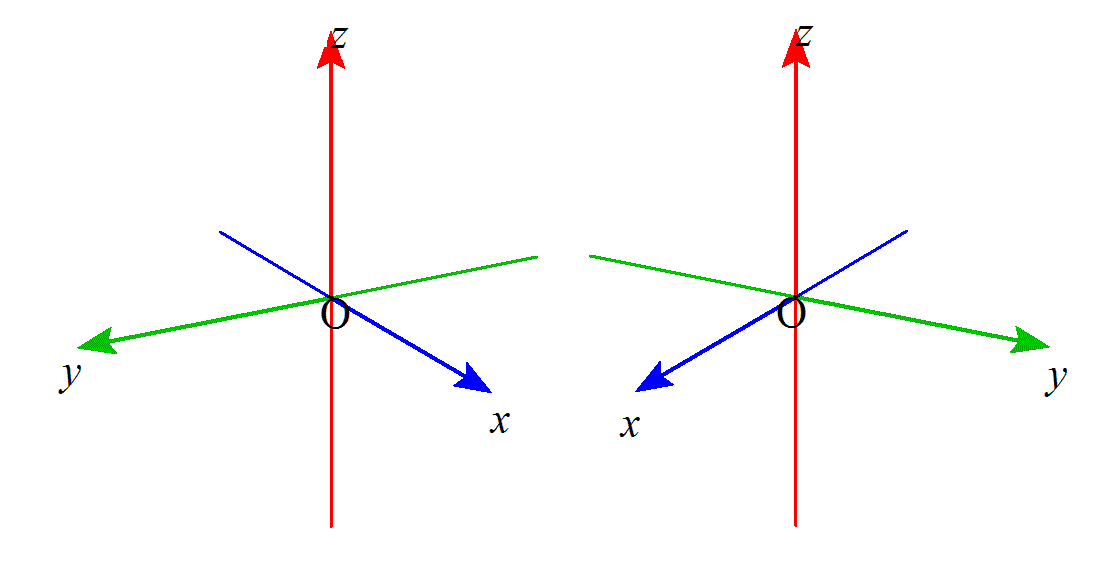
「右手の総則」は、「右手系」座標系において、xy平面上の「偏角」θの点(rcosθ,rsinθ)が、θが増大する方向への「回転」を表すベクトルをz方向にとる、というのだが、これは、そのまんま、「ベクトルの外積」の定義、
i×j=k
であって、いくら「近代ヨーロッパ」人、の考えることと言ったって(笑)、論理的過ぎて、疑わしい。
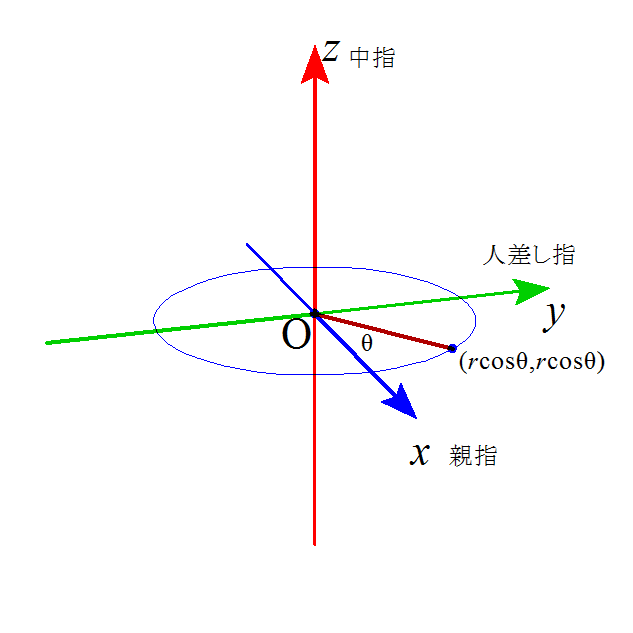
で、よくわからないままに、話を戻すと、スカラー量としての角速度の大きさと、同じくスカラー量としての速度の大きさとの関係は、前者に回転半径をかければ後者が得られる。半径Rで角速度の大きさωなら、単位時間にωRの「弧」の長さ分だけすすむ、これがそのまま速度の大きさであるから。

ならば、上の図のように、ベクトルOPすなわち、rと「右ねじの法則」によって定めた角速度ベクトルωのなす角をθとすれば、
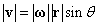
「方向」も加味して考えると、ωをrに重なるように回転させるとき右ねじの進む方向がvとなっているから、「外積」の定義にしたがい、
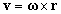
になっているわけである。成分であらわすと、

さて、ところで、おなじみ(笑)「ハミルトン演算子」∇は、
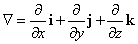
であるから、ここで速度ベクトルvの「回転rot」、すなわち、∇×vをつくってみると、
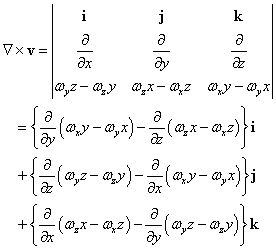
さらに、おっと、忘れていた!、ここで、角速度ωは「定ベクトル」としておく、手元の教科書でもそうなっているのだが、つまり、もしそうでなく、(x,y,z)の関数、つまり「ベクトル場」、であったなら、これからの偏微分計算が「収拾つかなく」(笑)なってしまう、という「能力上」の(笑)制限であるが、で、安心して続けると、

なんと、vの「回転rot」、すなわち、∇×vは、角速度ベクトルω、の2倍、を表していたのである。これが、「回転」の、「意味」、であった。
これで、「『発散』と『回転』の違いについて述べよ」、なる、森毅センセイへの「積年の」(笑)宿題は、完了したわけだが、今しばらく、「ベクトル解析」の勉強を続けて、できれば、「コーシー・リーマンの微分方程式」という、ほんの入り口だけを恐る恐るやってみた「複素解析」の話につなげてみたい、という野望を抱いている、「生きている」時間が、「間に合えば」(笑)、の話であるが、・・・。
「ベクトル場の線積分」に関して「グリーンの公式」というのがあって、それと、正則関数に関する「コーシー・リーマンの微分方程式」とを組み合わせれば、複素平面上での、「コーシーの積分定理」なる、きわめて美しい、いや、右辺がゼロなのだから、「美しい」の要素の一つに「単純さ」があるのなら、まことに美しい、その式を導いてみたいのであるが、その準備として、
- 「曲線」というものの表記の仕方、それに関連して「弧長」、「線素」の定義、
- そして、「スカラー場の線積分」、「ベクトル場の線積分」、の定義、
と、話を進める。
空間内の点P(x,y,z)を表す位置ベクトルrが、tなる媒介変数にともなって変化するとき、その軌跡はある曲線をなすであろう。すなわち、

r(t)が表わす点をP、少し離れたr(t+Δt)が表わす点をQ、とすると、Δt→0の極限において、ベクトルPQは、この曲線の「接ベクトル」を表すであろう。

tで微分することを、のちに「弧長」sを導入した際に混乱しないように、ベクトル記号の頭の上に「・」(ドット)をのっけた記号で表すことにする。
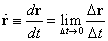
これが、曲線r(t)の「接ベクトル」である。
この曲線上、t=aから、t=bに至る部分の長さは、この区間をきわめて短いΔtに区切り、そのそれぞれの一方の端における「接ベクトル」の長さを足し合わせることになるだろうから、
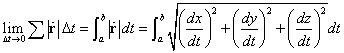
ここでもtによる微分を、頭の上「・」であらわすと、
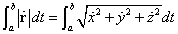
これがt=aから、t=bまでの、曲線の長さだとすれば、aから変数tに至る曲線の長さを、「弧長」なるtの関数として表記することもまた可能なり(笑)。すなわち、
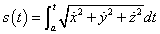
というわけである。両辺をtで微分して、
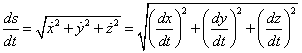
この辺の変形を私は、正確に説明できない(笑)のだが、形式的には、両辺にdtを「かけて」、
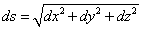
これを「線素」dsと呼ぶのは、高校の数学IIIの教科書にも、出てくる。
上で定義された「弧長」s自体を媒介変数として、曲線の式を書き直すと、やや面白いことが起こって、話がシンプルになる。
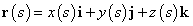
曲線がr(s)と表されることになるから、その「接ベクトル」も、変数sによる微分を、右肩に「´」(ダッシュ)であらわすと、
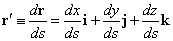
ここで改めて「弧長」を定義し直すと、このsを媒介変数とする「接ベクトル」の長さを、sが、0から、ほかならぬ(笑)s自身に至るまで足し合わせたものの極限であるから、
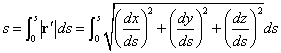
同様に、sによる微分を右肩「´」で表記すれば、
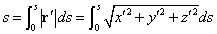
ところで、
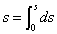
は自明の理(笑)、であるから、両式を見比べると、
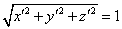
となり、つまり、
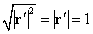
「弧長」sを媒介変数とした「接ベクトル」は、長さ1、すなわち「単位接ベクトル」であることがわかったのである。だから、今後、曲線を表す際には、「弧長」sを変数とするのが便宜、という訳である。
今日は、とりあえず(笑)、ここまで。
では、「スカラー場」の線積分。ほとんど忘れかけているので(笑)、「スカラー場」とは、なんであったか?、点(x,y,z)を指定したときに、それに応じてφなるスカラー量が返ってくる、「指定したこと」に対して、「答が返ってくる」、自動販売機の、どれかのボタンを押すと、「指定」した品物が取り出し口に出てくる、にも似て、「昔の」自動販売機は、今ほど「賢く」なくて、しかるべき大きさのコインが通過すると、通常たった一種類の品物が、機械仕掛けで押し出されて落ちてくる、これを「ペイ・ガムpay_gum」、お金を入れるとガムが出てくる機械、と呼んだから、「刺激」と「応答」、「入力」と「出力」のように、「一対一対応」の、関数関係を「ペイ・ガム理論」と呼んだりした。function「関数」の日本語訳も、当初は「函数」で、これは「函(はこ)」、中で何をやっているのかは実はよくわからない「箱」black_boxに何かを入れると、しかし、何かが出てくる、そんな由来ではないかと想像している。だから、その「函数」φのことを、「スカラー場」、と呼ぶのである。2次元平面でたとえ話をするならば、地図上の各地点に、たとえば昨日の気温が書き込まれている図面があったとしよう。温度は、方向をもたない「スカラー量」であるから、一面にスカラー量が書き込まれていて、「ここ」と指定すれば、「そこ」気温がわかるような「世界」であるから、「場」fieldと呼ぶのであろう。
前回定義したように、「弧長」sを媒介変数として、曲線r(s)を考える。
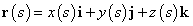
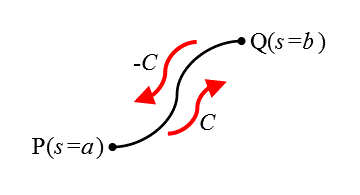
この曲線上のs=aにあたる点をP、s=bにあたる点をQ、と名付け、PからQに向かってこの曲線に沿って移動する「動き」を、Cと呼ぶ。反対に、QからPへの動きを、-Cとする。
このCなり、-Cなりが、「線積分」の「積分路」で、その指定した曲線上を、弧長sの微小変化Δsごとに、与えられた「被積分関数」の値を、加算していくのである。
これを、もう少し「ぶっきらぼう」に言うと、・・・、「ぶっきらぼう」、とは何か?、広●苑によると、「言動に愛嬌がないこと」、それはわかる(笑)、語源、由来、等についての説明は一切、なかった、・・・、
スカラー場φ(r)=φ(x,y,z)に対して、
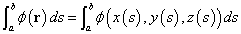
を、スカラー場φの、Cに沿った線積分、と呼び、以下のようにも、書く。
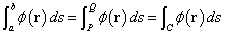
積分区間を逆転させれば、積分値の符号は逆になる道理はここでも通用するから、
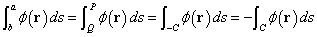
である。
かつて、この教科書で、私は大学院入試の準備の勉強をしたのであるし、記憶にないけど多少の書き込みもあるから、練習問題、なども解いたのであろう。でも、この話の「何」が、「新しい」、のか、多分、ちっとも、わかってなかった。それは今でも同じで、大して「わかった」わけではないものの、不思議なもので年を取れば、そ・れ・な・り・の、「知恵」はつく。
高校の数学IIの教科書を見てみれば、多分、「微分」に関しては、「平均変化率の極限」、「接線の傾き」という、具体的な想像が可能な「実体」と対応付けた「定義」が記されているのに対して、「積分」には、それが、ない。
ax2を微分したら、2axでしょ?、だったら、微分して2axになるような関数の集まりを、ax2+Cって書けばいいじゃない、それを「積分」っていうの!、つまり「微分」の「逆」ってこと!、としか、多分(笑)、言ってない。ようやく数学IIIになって、「区分求積法」なる、命名で、定積分というのは、曲線下の面積を、底辺Δxなる微小量に切り分けた細長い長方形の面積の和の極限、としてあらわす技法なのだ、という「意味」を、本当は、初・め・て・知るはずなのである。
で、高校の教科書に出てくる積分は、数学IIIの教科書の末尾に「こっそり」、曲線の長さ、が登場するものの、すべては、ここでの言い方に対応させるなら、x軸、なる「直線」に沿った「線積分」であった訳だ。
だから、何が「新しい」か?、というと、ここでは、積分路の指定の仕方によって、積分値が異なってしまう、という未曽有の経験をすることになる、それが「新しい」のである。そうして「積分」という言葉が、「面積」という「実体」から、少しだけ離れて、概念の「拡大解釈」、「抽象化」の入り口に立つことになるのであろう。
2次元の複素数の世界の中で、積分は関数の変化を、1次元の曲線に沿って追っていくことになった。コーシーの積分定理の示していることは、正則関数に対しては、C1,C2に沿って変化を追ってみても、積分として総合されて得られた情報は同じものだったということである。積分のはたらきは、実数から複素数へと移り、正則関数の上で適用されることになると、完全に‘量の世界’から脱してしまった。
「数学という学問II」志賀浩二(ちくま学芸文庫)
さらに複素平面に話が進めば、もうひとひねりの「抽象化」を経験することになる「予定」なのだが、それはまだ、先の話だ。
「例題」をやってみる。
ともに、xy平面上の2点、P(-1,0)、Q(1,0)を両端とする曲線なのであるが、一方のC1は、x軸上を、他方のC2は、原点を中心として半径1の円周上を、第II象限から第I象限へと、それぞれたどるものである、と定義する。
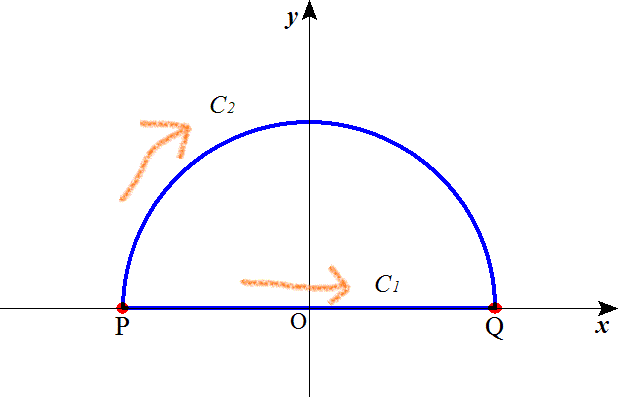
スカラー場φ=x+yに対して、それぞれ、C1に沿った線積分をI1、C2に沿った線積分をI2、と呼ぶことにする。すなわち、
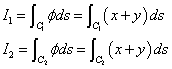
C1に沿って考えると、「弧長」sは、P(-1,0)においてs=0、Q(1,0)においてs=2、だから、
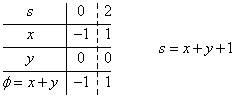
φ=x+y=s-1なる「変数変換」、「置換積分」を行って、
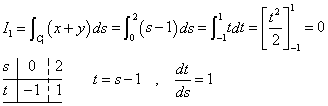
を得る。馬鹿丁寧(笑)過ぎるが、さらにt=s-1なる「置換積分」をほどこした。
C2上の動点を、(cosθ,sinθ)とすると、
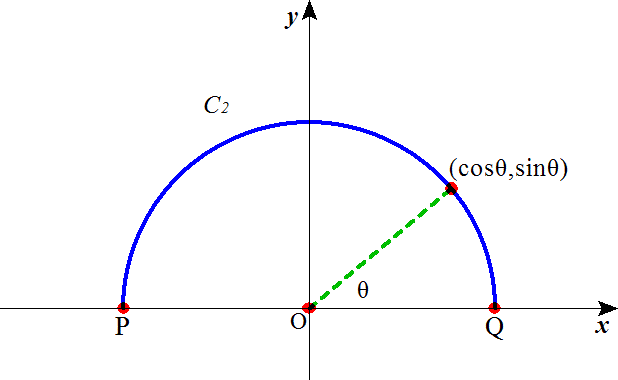
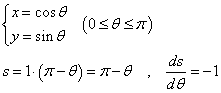
という対応関係が得られるから、
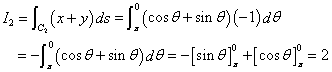
となって、ともあれ、「積分路」によって、積分値が異なる、ことは、「経験」できたわけである。
「ベクトル場の線積分」、に進む。
「弧長」sを媒介変数として、曲線C:r=r(s)が、あったとする。無論、これだけでは、「何のことやら、さっぱり」(笑)、わからない。平たく言うと、なら、最初から「平たく」言え!、ただ一つの変数sを含む等式があって、sを定めると、それに対応する、位置ベクトルr(s)であらわされる点が得られ、それらの点をつないでいくと、ある曲線になるのだ、それをCと呼ぼう。ほら、わかりやすいじゃないか!
次に、「ベクトル場」a(r)=axi+ayj+azkが、あったとする。今度は、別に曲線C上でなくても構わない、ともかく、ある点rを指定すると、それに対応する「ベクトル量」aが得られる、としよう、と言っている。
rを、「弧長」sで微分すると、そのベクトルの長さは自動的に1になってしまうことはすでに確認した、だから、これを「曲線」Cの「単位接ベクトル」、と言うのであった。
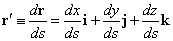
ベクトルaと、ベクトルr´の「内積」を求めると、これは「スカラー量」であるから、ここに、新たに「スカラー場」a・r´が、得られた、ことになる。位置ベクトルrであらわされる点を指定すると、それに対応して、一つの「スカラー量」が得られることを、そう呼ぶのであった。すなわち、
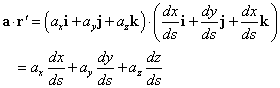
この「スカラー場」a・r´の、曲線Cに沿った線積分をもって、「ベクトル場」aの、曲線Cに沿った線積分、と呼・ぶ・、のである。すなわち、
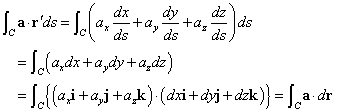
と、これは、様々な表記法がありうる、と言っているだけのこと(笑)である。
これにて「ベクトル場の線積分」の定義は、終わった(笑)。これについて、「グリーンの公式」なる積分公式を、導くのは、次回以降の課題として、今日は、せっかくだから、この「ベクトル場の線積分」の、物理学的な「意味」を、また、同じく、「万有引力」で、説明してみたい。
私たちが「生きている」、と、常日頃「感じている」ミクロ世界では、重力は常に「足もと」、z軸負方向、を向き、大きさは、mgである。これが、左図。
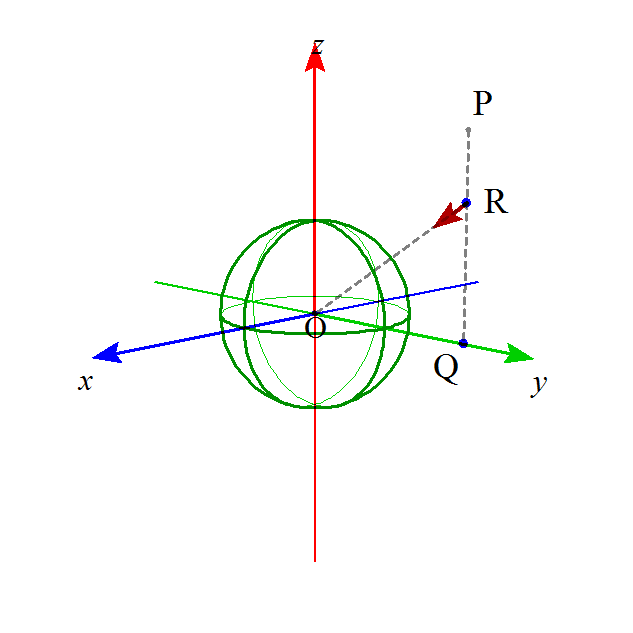
ずうっ〜と、「視点」を下げ、地球の外側のどこか「彼方」にもっていくと、そこから眺めたマクロ世界では、その力は地球の中心に向かい、大きさは、地球の中心からの距離rとして、GMm/r2であって、したがって、場所が移動すれば、その「ベクトル量」としての大きさ、向き、ともに、異なるのであった。これが、右図。
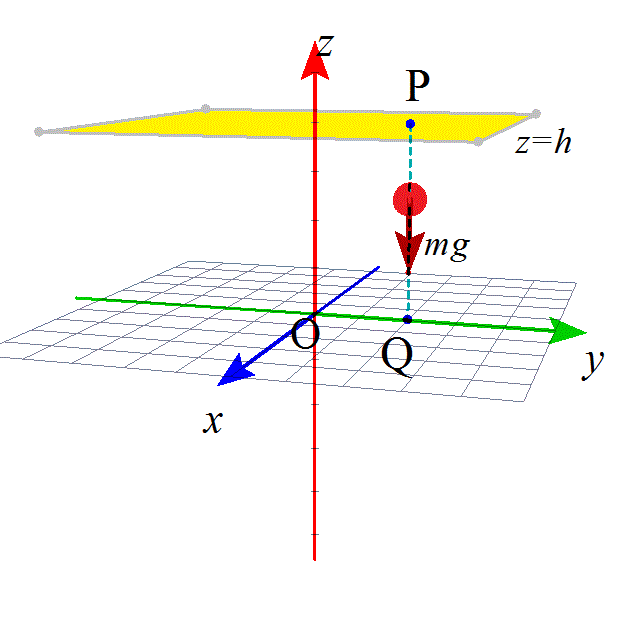
曲線Cを、定める、のであった。yz平面上の「線分」PQが、それ、であることにしよう。P(0,a,h)、Q(0,a,0)として、弧長sは、Pにおいてs=0、Qにおいてs=h、とすれば、この線分上の動点をあらわす位置ベクトルrは、
r=(0,a,h-s)=aj+(h-s)k
と、書けるであろう。ならば、これを弧長sで微分したものが、曲線Cの単位接ベクトルr´、であるから、

ここに「ベクトル場」を導入するのであるが、これが、上の二つの場合「ミクロ世界」と「マクロ世界」とで、異なる形式をもつことになる。点を指定すると、あるベクトル量が得られる、これが、繰り返すが(笑)、繰り返すのは、「話者」が頭が悪いからである(笑)、「ベクトル場」であった。「万有引力・または・重力」は、「力」なるベクトル量であるから、これを記号fで表すとすると、
- 「ミクロ世界」では、どの点を指定しても・、つねに下向き、つまりz軸負方向、大きさmgであるから、
f=-mgk
したがって、
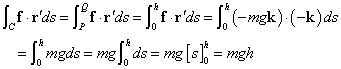
ほら、なんと、これは、P点における「重力による位置エネルギー(ポテンシャル)」そのもの、別の言い方をすると、質量mの物体がPからQまで。「曲線」Cに沿って、移動した際に、重力がした「仕事」を表しているのである。
- 「マクロ世界」では、どうか?、ここでは、指定された点の位置によって、「ベクトル場」fが異なってくる。PQ上の動点、位置ベクトルrが表わす点をRと名付けよう。
∠ROQ=θとすると、

したがって、点Rに存在する質量mの物体に作用する万有引力fは、
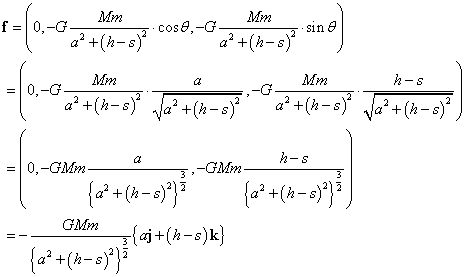
ならば、
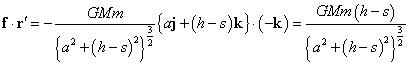
では、積分を行う。
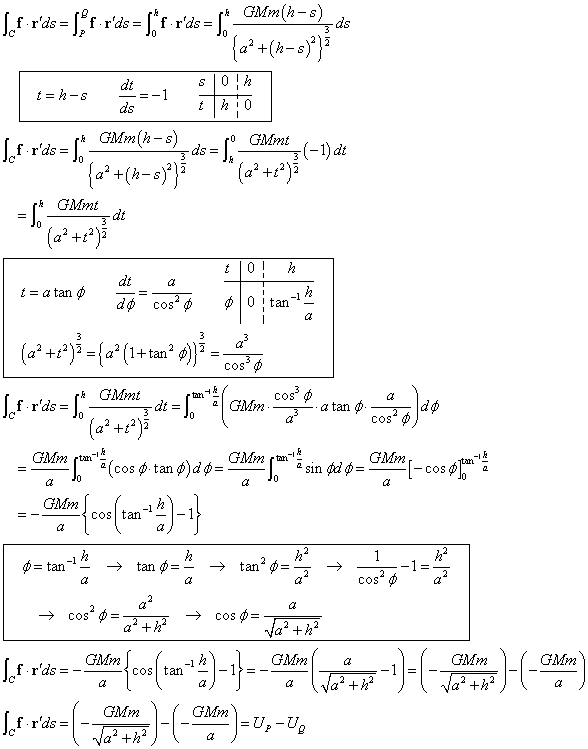
長い話であったが、置換積分を二回ばかりほどこすことで、何とかなったのである。何とかなったからこそ、「偉そうに」書いてみたのであるが、・・・。
何がわかったか?、やはり、P点における「万有引力による位置エネルギー(ポテンシャル)」UPと、点Qにおけるそれ、UQとの「差」にあたるエネルギーが、質量mの物体が曲線Cに沿って移動する間に、「万有引力」のした仕事として、与えられた、それが、この積分の表す「意味」なのであることが、分かった、のである。
では、「グリーンの公式」。
xy平面において、単一閉曲線Cで囲まれた領域をDとする。
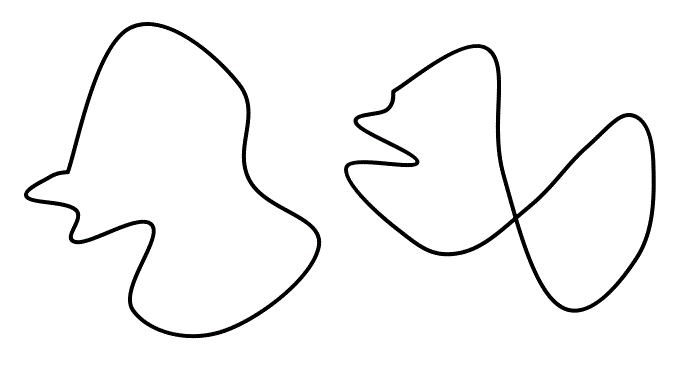
ここに「単一閉曲線」とは、上図の左のようになものであって、右のようなものでな・い・、もののことだ(笑)。ねじれていてはいけない。「裏返す」と言う「位相的変形」を伴わずに、「円」と一対一対応が付けられる図形のこと、である。
その、xy平面において、単一閉曲線Cで囲まれた領域をD、において、
ベクトル場 と、その偏導関数が、CおよびD上で連続であれば、
と、その偏導関数が、CおよびD上で連続であれば、
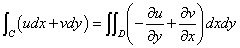
これが、「グリーンの公式」、なのだそうである。
ここでは、簡単のため、と人はよく言うが(笑)、もちろん、ここでは、「簡単なこと」し・か・できないから、そうするのである、・・・、もっとも単純な「単一閉曲線」として、「長方形」を取り上げる。微分積分額の教えるところ、あらゆる曲線は短く切れば直線であるように、あらゆる曲線で囲まれた図形は、長方形の組み合わせで表現できるからである。
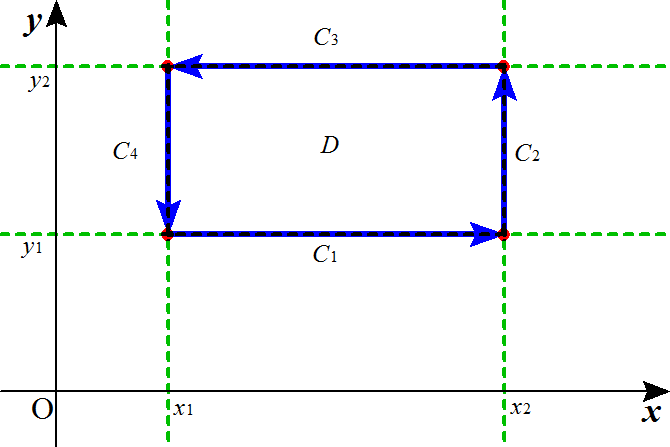
さて、「単一閉曲線」Cを、矢印のように、順次C1、C2、C3、C4、と、「反時計回り」に回り、その曲線に沿った線積分を考えることにする。
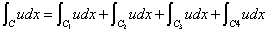
であるが、C2とC4においては、dx=0であるから、その積分値はゼロ、
また、C1では、x1からx2の積分であるのに対して、C3では、積分区間が逆転しているから、
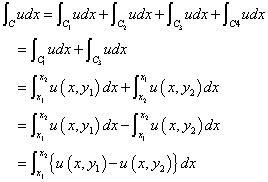
ここで、u(x,y)は、x,yを含む2変数関数なのであるが、C1上では、yは、定数y1に固定され、C3上では、yは、定数y2に固定され、ているのである。
一方、右辺の「多重積分」を、まず、yの、次にxの積分、という風に分解していくと、
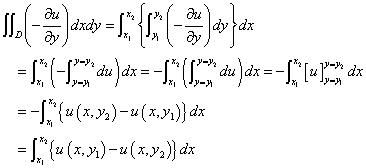
と、なるほど、同じものになった!、同様に、
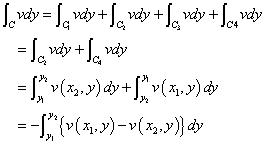
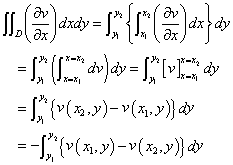
これで、もっとも単純な、長方形という「単一閉曲線」については、「グリーンの公式」、
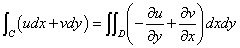
が、証明できたわけである。これを、「拡張」する。
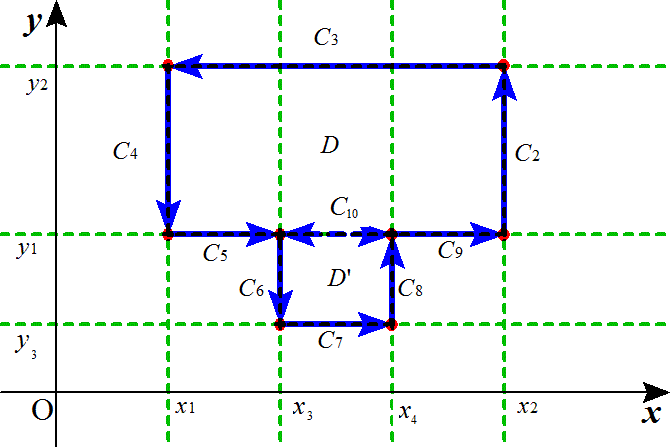
C5,C10,C9,C2,C3,C4なる「単一閉曲線」Cで囲まれる領域をD
C7,C8,C10,C6なる「単一閉曲線」C'で囲まれる領域をD'
として、「反時計回り」の線積分を考えると、
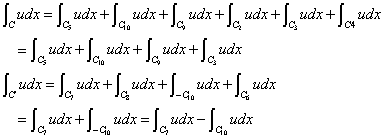
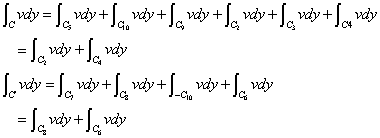
したがって、
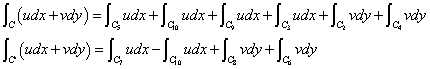
CとC'をつなげた「単一閉曲線」の「反時計回り」の積分を次のように書けば、
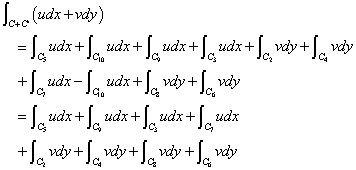
さらに細かく、積分区間を分割してみると(笑)、
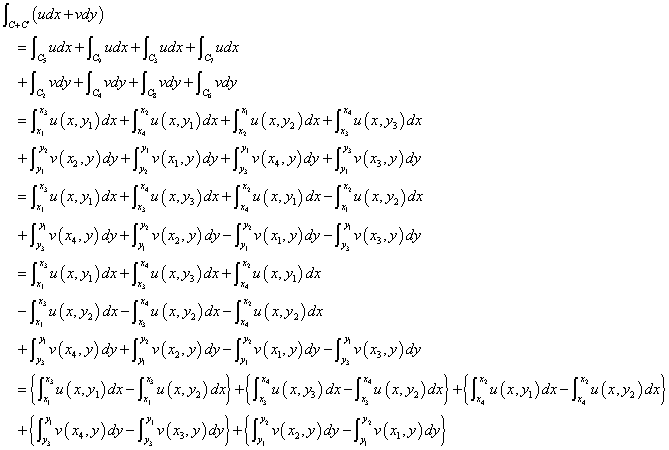
中カッコでくくった2項ずつは、「グリーンの公式」によって、

もう、何やってんだか、だんだん、わからなくなってきたが(笑)、とにかく、なんとか、なったよ。ほら、「グリーンの公式」が、二つの長方形を合体した「単一閉曲線」に、拡張されている。以下、同じことを、繰り返していけば(笑)、一・般・の・「単一閉曲線」についても、同じことが言える筈、なのである。
私は、ちっとも「理系」の出身者として「身を立てた」(笑)、訳でも、「名を成した」(笑)訳でもないのだが、それでも、「理系」特有の感覚、アルチュセール(笑)の言うところの、「自然発生的イデオロギー」であろうか?、「数式」上の結論が出てしまえば、「納得」してしまう、ところがあるようで、前回の、なんじゃこれは?、数式エディタ広げたまま、眠くて眠くて仕方なくなったから、放り出してやめただけなのだが、確かに、あっていなくもない(笑)が、なんの「説明」にもなっていないではないか?、「数式」の方が、「自然言語」より、多くを、しかも、正しく、「語る」ことができる、というのが「イデオロギー」かも知れない。私たちは、「自然言語」によってしか、「理解」することはできないのに。「自然言語」によって付着された「意味」を、ときおり引き剥がすことが、劇的な視野の展開をもたらしてくれ、それが例えば「数学」の、汲めども尽きせぬ「喜び」の源泉ではあるのだけれども、・・・。
もう少し、まともな説明を考えてみる。もっとも単純な「単一閉曲線」、長方形に関しては、「グリーンの公式」は示された。
この長方形に隣接して、一片を共有するように、別のもう一つの長方形を用意する。
長方形の周囲を「回る」際、「上から」、つまり「右手系」座標軸のz軸正方向から眺めて、「反時計回り」になるものを「正」と定めた。そうでなくてもよかったはずである。ここでの「線積分」なるもの、「面積」などという何か「実体」と関連付けられている訳ではないから、その値が正なのか負なのかは不問に付されている。ただ、「約束」は、決めた以上一貫していないと、どこかで正負が逆転し、支離滅裂になることになる。

すると、この長方形、はじめに考えた「上」の方の領域Dの方では、C10なる「曲線」に関して「順方向だったのに、新たな長方形、領域D'については、「逆方向」、ならば、Dに「グリーンの公式」を適用して得られた積分結果と、同じくD'から得られた結果を合算すれば、C10区間に関するものが、正負異なるから相互に打ち消しあってしまって、ということは、二つの領域の「境界線」が、消えてなくなってしまい、文字通り、二つの領域が「つながった」ことになるではないか?、それは、「グリーンの公式」が、二つのバラバラの長方形ではなく、それらが合体した、「凸」という字をひっくり返したみたいな形の図形に関しても、適用してよい、ってことになるのではないか?
で、このような「操作」を、繰り返していくならば、究極的には、どんな複雑な形であっても、「単一閉曲線」で囲まれる領域である限り、「グリーンの公式」が成り立つ、と言えることになるではないか?
これでいいのかな?
次に進む。前に少しさわりだけをやったが、「さわり」しかできなかったからだが、「複素解析」の復習、・・・。
- 「正則関数」の定義
複素平面上の領域Dにおいて、関数f(z)が微分可能で、導関数f'(z)が連続であれば、f(z)は、領域Dで正則である、という。
点z0を含むある開集合でf(z)が正則であれば、f(z)は点z0で正則であるという。
- [定理]:関数f(z)=u(x,y)+iv(x,y)が正則であれば、u,vは連続な偏導関数をもち、次の「コーシー・リーマンの微分方程式」を満たす。逆も成り立つ。
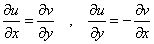
ここで、複素平面上の領域Dで定義された「正則関数」f(z)に対して、次の如き「コーシーの積分定理」が知られているのだが、これが、「グリーンの公式」によって、「難なく」(笑)、証明できるとの運びなのである。
- コーシーの積分定理
f(z)は、領域Dで定義された「正則関数」、Cは、D内の単一閉曲線とすると、
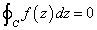
このインテグラルの記号に「○」印が付されたのは、「単一閉曲線」に沿った線積分、の意だそうである。それにしても、「シンプル」である。なにせ、右辺は、「ゼロ」なのだから、・・・。
やってみる。
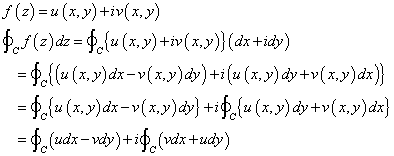
この積分の、実部、虚部、それぞれに対して、以下の「グリーンの公式」を適用する。ベクトル量の「成分」がスカラー量であるように、複素数の、実部、虚部の係数は、それぞれ実数であるから、問題は、ない(笑)。
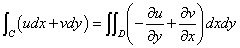

そして、f(z)が、「正則関数」であることから、上の「コーシー・リーマンの微分方程式」、を持ち出すのである。
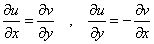
こうして上式の被積分関数は、二項とも、恒等的にゼロになってしまったから、だから、積分値もゼロなのであった。
無論、私には、その「意味」を、述べることはできないが(笑)。この後、もう少し、「複素解析」に、素人なりに(笑)、深入りして、今度は、よく似た名前だが、「コーシーの積分公式」、を証明したい、と思う。
「ベクトル解析」も、頓挫している。この先「面積積分」に入って、「ガウスの法則」まで行きたい、と思う。そうこうするうちに、「Amaz●nマーケットプレイス」から、「ゲーデル・エッシャー・バッハ」が届いてしまった。論理学を少しかじったものだから(笑)、この二十年前の、いかにも「バブリー」な、・・・、定価5,500円もする!、当時、私は、「●●出版社」なる、ほぼ、ありもしない会社の「編集長」なる名刺を持ち歩き、銀座のクラブ(?)とやらで、ブランデーに三杯位か、と、クリームチーズとピーナツが皿に載っていたか、それで多分10万円くらいの支払いを、他人が「アメッ●ス・ゴールド・カード」で済ませるのを「当然」のように「傍観」(笑)し、「無制限タクシーチケット」を奪い取るようにして受け取って、高速道路で帰宅した、りしていた、ものだ、MCエッシャーの展覧会があると聞けば出掛けて高い図録を「ぽぉーっん」と買い、売り出されたばかりの30万円もしたCDプレーヤーと、「素養」がないから、知りもしない(笑)、ピアニストのグレン・グールドと、古生物学者の、スティーブン・J・グールドの区別もついていなかった、そのグールドの、J・S・バッハ、一枚3000円もするCDをこれまたいくつも「ぽぉーん」と買い、・・・、でも、やっぱり「知性」はお金で買えなかったCan't_buy_me_love、みたいで、その書物の大半は理解できなかったから、・・・、こうして「貧しい」老後の暇つぶしに、読み直してみることにしたまでである。「時間」が、「間に合えば」、の話であるが、・・・。
では、次は、「コーシーの積分公式」。繰り返すが(笑)、人は、何か、決して喋ってはならないことがあるときに、まさにそのことを決して喋らないために、何かほかのことについて、饒舌になるのである。つまり、興ざめなことを言えば(笑)、私は、少しも「コーシーの積分公式」などに、興味は(笑)、ない。それでも、数式の変形に没頭してしまえば、しばし時を忘れ、何か「興が乗った」如き錯覚が訪れる。「現実」に、何らの具体的対応物をもたない「数学」の、それが、「治療効果」、なのである。
準備が少し必要で、まず、
複素平面上の、中心z0、半径ρの円をCとするとき、
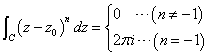
を示そうと思う。
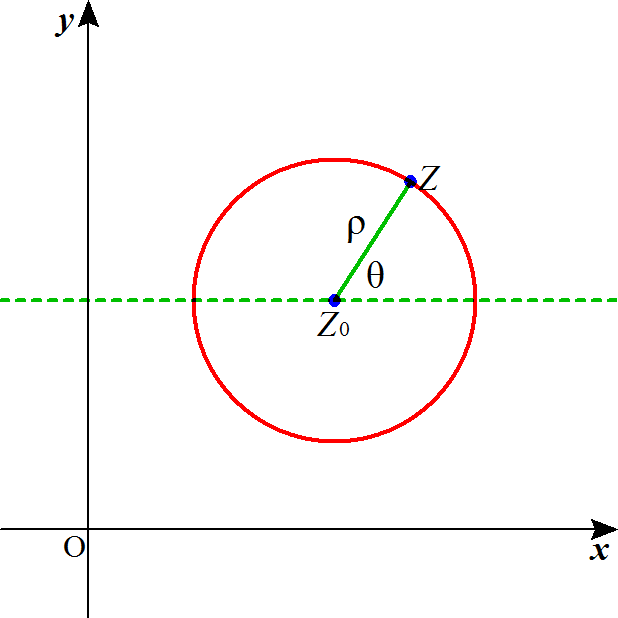
z-z0は、媒介変数θを用いて、
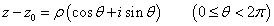
と書けるから、この積分は、置換積分によってθの積分として計算ができるだろう。その前に、複素平面の「世界」では、「オイラーの公式」により、三角関数と指数関数が、不気味な関係でつながりあっていることは、以前、お話をした。吉田武「オイラーの贈り物」(ちくま学芸文庫)は、ただその一行の「公式」を導くために書かれているのだ。すなわち、
eiθ=cosθ+isinθ
これを用いると、
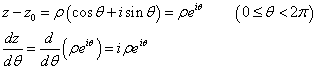
したがって、求める積分は、
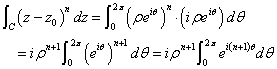
ここで、n=-1のときは、被積分関数は定数となる特別な場合であるから、場合分けをしなければならず、
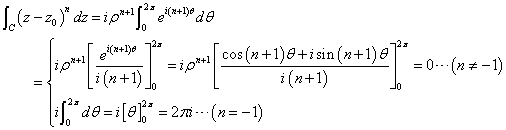
という訳であった。なんだか、「不気味」な結論である、という以外に特に「感想」はなく(笑)、無論、その「意味」を説明したりできるわけが、ない。
で、「コーシーの積分公式」に移る。
複素平面上の領域Dにおいて、正則な関数f(z)がある。D内の「単一閉曲線」Cに沿った線積分を考える。

とのことで、これが「コーシーの積分公式」だそうなのである。
相変わらず「不気味」以外の感想はないが、そう不気味がってばかりいても話が進まないので(笑)、注意を要するのは、左辺の被積分関数が、z=z0では定義されないから、当然にも、領域D内で「正則」などとは言えないことである。だから、もちろん、右辺は0ではない、つまり、このままでは「正則」でない点を含むから、「コーシーの積分定理」は使えない、ということだ。いかにも「頭の悪そうな」(笑)、説明で、申し訳ないが、・・・。
そこで、どうやら、この「切り紙細工」みたいな「トリック」が、「複素解析」の「醍醐味」であるらしいことは飲み込めてきたが、「醍醐」は、今日でいうヨーグルトのようなものであるらしい、古代、この島に遠来の旅をしてきた者たちの中には、北方の遊牧民族もいたであろう、牛や山羊や羊の乳を食用にしていたであろう、腐敗菌が繁殖する以前に、乳酸菌を優占種として繁殖させ、発酵させれば、長期保存に耐えることも知っていたであろう、牧畜を知らないこの島の住民は、その妙なる味を、こう呼んだのであろう。
では、領域D内に、ことさらにz0を含まないような、以下のような「単一閉曲線」を、無理矢理、作ればよろしい。z0を囲むC'は、z0を中心とし、半径εの小さな円だとする。そして、もともとのCにも、C'にも、小さな「隙間」を穿ち(うがち)、そこを往きはC1、帰りはC2、なる線分で、「橋を架ける」わけだ。「隙間」はとても小さいから、C1、C2、は、お互い積分区間が逆転した同じ積分、と見ていいから、プラス・マイナスで、「キャンセル」される!、という訳だ。さらに、C'、に沿った積分に関しては、z0を中心とし半径εの円、なのだから、上で準備したものが使えそうであろう?、ただし、回転方向が「時計回り」だから、符号が逆であることに注意を要する。
始めよう。左辺の被積分関数は、Dからz0を除いた領域、D'、下の図の色をほどこした部分、では「正則」であるから、「コーシーの積分定理」が成立する、すなわち、
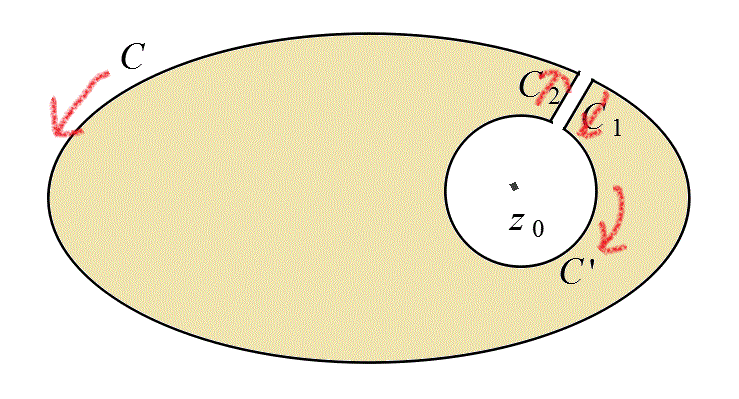
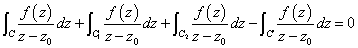
第4項に負号がついているのは、上にのべたようにC'での線積分のまわり方が「時計回り」だからである。さらに、C1とC2の積分が、打ち消しあうことから、
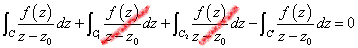
すなわち、

ここで、上で示した式のうち、n=-1のときのものを使う。
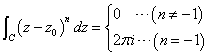
この式は、見ればわかるように(笑)、円Cの半径ρを含んでいない、ということは、いかなるρに対しても成立する、ならば、十分小さいものでもよいではないか?
したがって、z0を中心として半径εの円たる「単一閉曲線」C'に対して、εを無限に小さくした場合にだって、右辺の値は、通用するはずなのである。すなわち、

ところで、εを限りなく小さくしていくと、円C'は、ついにはたった一点z0のみを含むものになってしまうだろうし、その極限においては、zは、z0になってしまうであろう。つまり、
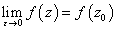
であるからして、先の積分は、
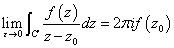
だから、もう一度丁寧に書くと、εがゼロに近づこうがどうだろうが、積分値には関係ないのだから、次の式が成り立つ、から、これで証明できたことに、なっている!
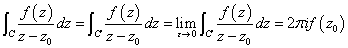
話を「複素関数」から、「ベクトル解析」へ、ちょっと戻して、だいぶ前だが、
- 曲線Cの方程式を定め、ここから、「スカラー場の線積分」、「ベクトル場の線積分」を定義したのだった。ならば、次は、
- 曲面Sの方程式を定め、ここから、「スカラー場の面積分」、「ベクトル場の面積分」に、
進むことになる。おそらくその彼方に(笑)、「ガウスの法則」が見えているような気がする。「世界」は、いたるところで、「逆二乗法則」の支配を受けているらしいのだが、万有引力しかり、電場に関するクーロンの法則、磁場に関するクーロンの法則、しかり。どうしてそんなことが起こるんだろう?
前にも同じ話をした。シャボン玉を想像してみたまえ、ストローの先端に石鹸水をつけて息を吹き込んで膨らます。石鹸水の液滴に、N個のせっけん分子が含まれていたとしよう。ある瞬間、膨らんだ球の半径が、rであったとすれば、その表面積は4πr2、そこに「均等に」せっけん分子が分布するであろうと、当然、いや、そうでない「理由」がないからな、仮定すると、単位面積当たりのせっけん分子数は、N/4πr2、ここでさらに息を吹き込んで、「しゃぼん玉」が膨張し、その半径が、krに拡大したとする。表面積はk2倍に拡大するから、その分、せっけん分子の面積に対する密度は、k2分の1に、減少するではないか?、これが、(笑)、「逆二乗法則」、である。
では、このような「世界」を記述する「モデル」には、何か「源」sourceから、「発する」矢印、例えば、「裸電球」、から発する「光線」、を、海の底で、あらゆる方向からの外敵に対抗すべく伸ばされているウニの針のように、見立てればよい。裸電球で照らされた部屋では、光源からの距離が離れるにしたがって、暗くなるだろう?、その暗くなり方が、おそらく、距離の二乗に反比例するのである。
- 「この世」にたった一つ、大きさQなる電荷があったとする。その場所を原点とし、そこからr離れた場所に、舌の根も乾かぬうちの(笑)嘘であるが、別のqなる電荷を置く。「この世」にただ一つ、なる但し書きは、この、後から付け加えた方の電荷が、もともとあったものに比べて問題にならないほど小さく、「場」に影響を及ぼしはしない、という話にしたいからである。新たに置かれたqには、電場に関するクーロンの法則により、
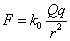
なる力が作用する。距離の二乗に反比例するこの「量」を、上の「裸電球―ウニ」モデルに徴して、単位面積あたりに、これだけの本数の「矢印」がある、と、呼べば、では、そもそもの「源」から、一体何本の「矢印」が出ていたことになるであろうか?、これをN本とすれば、表面積4πr2の球面上の単位面積あたりにこれだけの本数があったのだから、
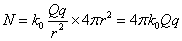
ということになろう?
- 「この世」にたった一つ、大きさMなる質量の物体があったとする。その場所を原点とし、そこからr離れた場所に、舌の根も乾かぬうちの(笑)嘘であるが、別の質量mなる物体を置く。「この世」にただ一つ、なる但し書きは、この、後から付け加えた方の物体の質量が、もともとあったものに比べて問題にならないほど小さく、「場」に影響を及ぼしはしない、という話にしたいからである。新たに置かれたmには、万有引力、
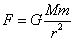
なる力が作用する。距離の二乗に反比例するこの「量」を、上の「裸電球―ウニ」モデルに徴して、単位面積あたりに、これだけの本数の「矢印」がある、と、呼べば、では、そもそもの「源」から、一体何本の「矢印」が出ていたことになるであろうか?、これをN本とすれば、表面積4πr2の球面上の単位面積あたりにこれだけの本数があったのだから、
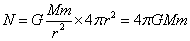
ということになろう?
こうして、例えば「電場」も、「重力場」も、もちろん決して目には見えない、仮想的な「矢印」で、満たされた空間なのだ、という「理解」が可能になった訳である。
では、始める。曲面Sの方程式、二つの媒介変数u,vを定めれば、曲面を特定できるから、
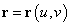
ここで、
- vを固定してuのみを変化させると、それは当然にも「曲線」になるから、これを、S上のu曲線、
- uを固定してvのみを変化させると、それは当然にも「曲線」になるから、これを、S上のv曲線、
と呼ぶ。u曲線、v曲線の「接ベクトル」は、
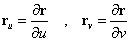
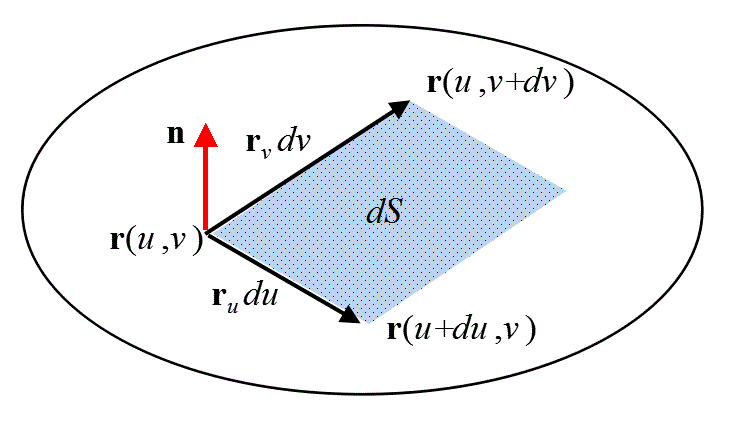
u曲線に沿って、点r(u,v)から、点r(u+du,v)まで、移動した経路は、duが十分小さければ、線分と見ることができ、ベクトルrudu、と書けるだろう。同じく、
v曲線に沿って、点r(u,v)から、点r(u,v+dv)まで、移動した経路は、dvが十分小さければ、線分と見ることができ、ベクトルrvdv、と書けるだろう。
これら二つの線分を隣接する二辺とする平行四辺形の面積を、dSと置けば、面積を「スカラー量」として扱うなら、これは、これら二つのベクトルの「外積」ベクトルの「大きさ」であろうし、
dSなる「ベクトル量」と見るなら、同じくこれら二つのベクトルの「外積」ベクトル、そのもの、となるであろう。前者を「面積素」、後者を「ベクトル面積素」と称す。
面積素:dS=|rudu×rvdv|=|ru×rv|dudv
ベクトル面積素:dS=ru×rvdudv
さて、「スカラー場の面積分」。「場所」rを指定すると、それに対応する「スカラー量」φ(r)が、「返ってくる」、これを「スカラー場」と呼ぶのだった。
(なめらかな)曲面S上の、(連続な)スカラー場φ(r)=φ(u,v)がある。Sに対応する領域をDとすれば、
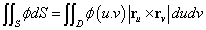
そして、「ベクトル場の面積分」。「場所」rを指定すると、それに対応する「ベクトル量」a(r)が、「返ってくる」、これを「ベクトル場」と呼ぶのだった。
(なめらかな)曲面S上の、(連続な)ベクトル場a(r)=a(u,v)がある。Sの単位法ベクトルををnとすれば、
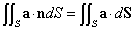
ということである。特に感興は(笑)、ない。「左様か?」、という感じ。な〜んにもわからんからね。こののち、「ストークスの公式」というのがあって、これは、2次元平面における「グリーンの公式」の、3次元化、なのだ、といわれる。その先に「ガウスの発散公式」が、ありそうである。
「ストークスの公式」、なめらかな閉曲線Cと、それを境界とするなめらかな曲面Sにおいて、ベクトル場、
a(x,y,z)=axi+ayj+azk
およびその偏導関数が連続であるとき、
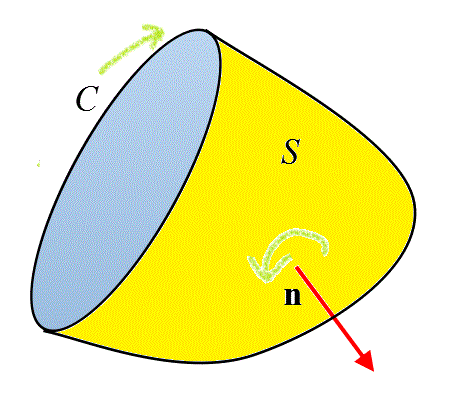
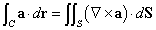
だそうである。参照しているのは、35年以上前、学部学生の3年次配当科目だったが、もちろん私は、卒業間際の4年で受講したはずの、工業数学、だったか、応用数学だったか、そんな感じの授業の教科書なのだが、証明は省略されていて、お莫迦な学生には無理だろう、と思われたからだろうし、だから、今の私にもやはり無理であろうから(笑)、諦めて、・・・、この「ストークスの公式」が、「グリーンの公式」の2次元から3次元への「拡張」であることを、確認することで満足(笑)しよう。
「グリーンの公式」、単一閉曲線Cで囲まれた領域Dにおいて、ベクトル場、
a(x,y)=axi+ayj
およびその偏導関数が連続であるとき、
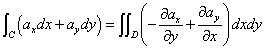
まず、
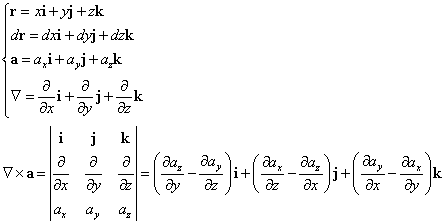
として、「ストークスの公式」を書き下すと、
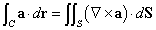
左辺は、
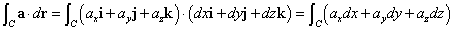
右辺は、
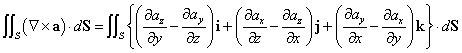
ここで、「ベクトル場の面積分」の定義を思い出すと、
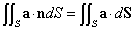
曲面Sの単位法ベクトルnが、x,y,zの各軸となす角をそれぞれ、α,β,γとおくと、
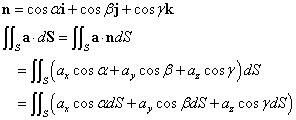
ところで、例えば、cosαdSというのは、dSなる微小な曲面を、その法ベクトルがx軸となす角がαだというのだから、x軸と垂直な面すなわち、yz平面に投影した「正射影」、すなわち、dydzなる、微小な長方形の面積、に他ならないだろう。他の2軸についても同じことが言えて、
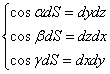
これを用いて、
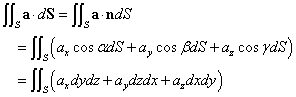
この関係を、「ストークスの公式」の右辺にも用いよう。
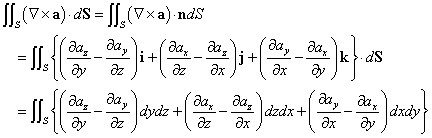
左辺と右辺をつなぐと、
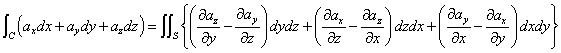
ここで、実は、閉曲線Cも、それを境界とする曲面Sも、みんなxy平面内にあるのだ、・・・、本当は立体なのに、それを「押しつぶして」しまうと、「グリーンの公式」に「なる」、筈だ、ということを言いたい。
xy平面内ならば、z=0だろう?、ならば、dzもゼロだろう?、上式のdzを含む項をすべて消して、
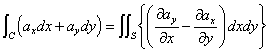
うわぁ!、なるほど、「グリーンの公式」、そのものではないか?
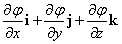
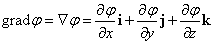
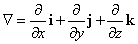
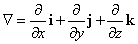
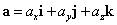
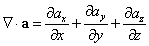
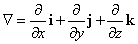
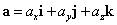
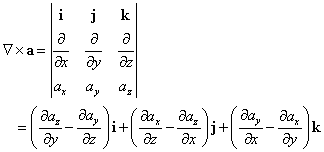

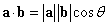
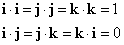
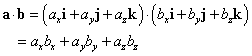

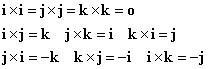
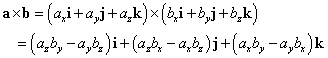
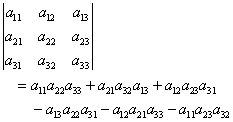
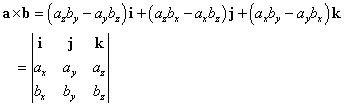

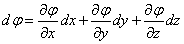
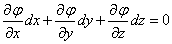 ・・・(1)
・・・(1)
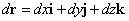 ・・・(2)
・・・(2)
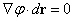
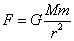



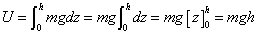
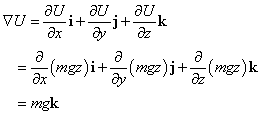
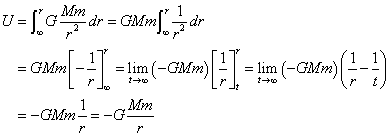
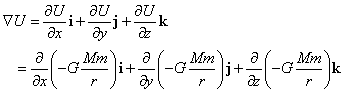
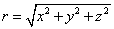
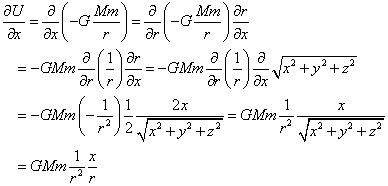
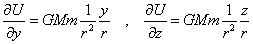

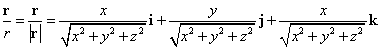
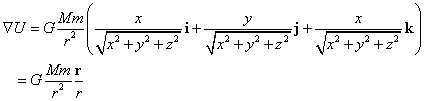

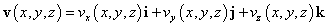


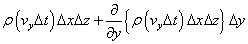
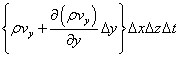
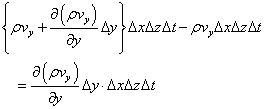
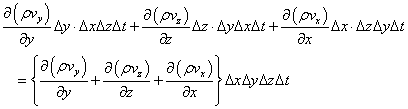
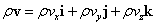
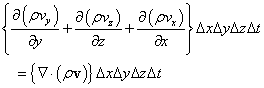
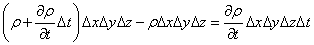
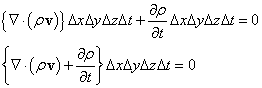
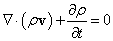




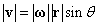
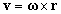

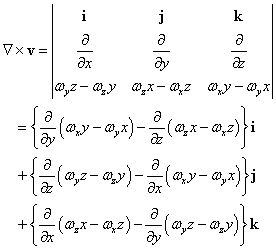



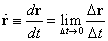
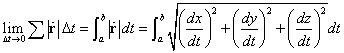
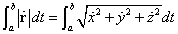
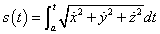
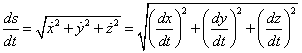
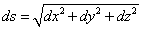
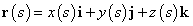
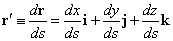
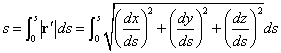
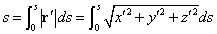
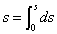
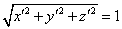
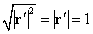

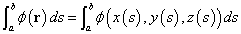
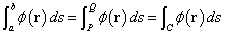
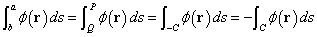

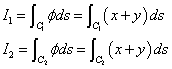
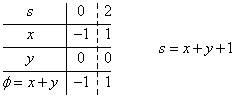
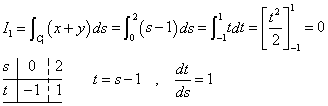

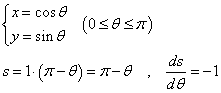
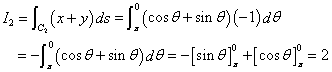
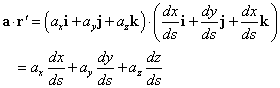
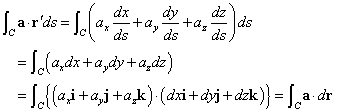



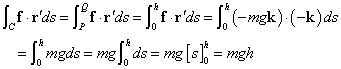

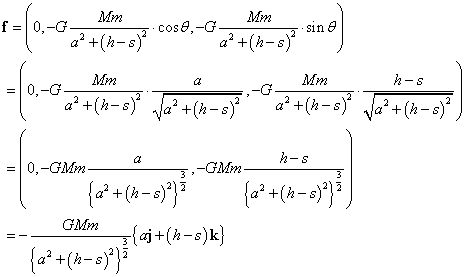
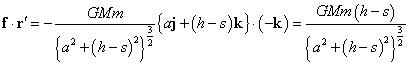
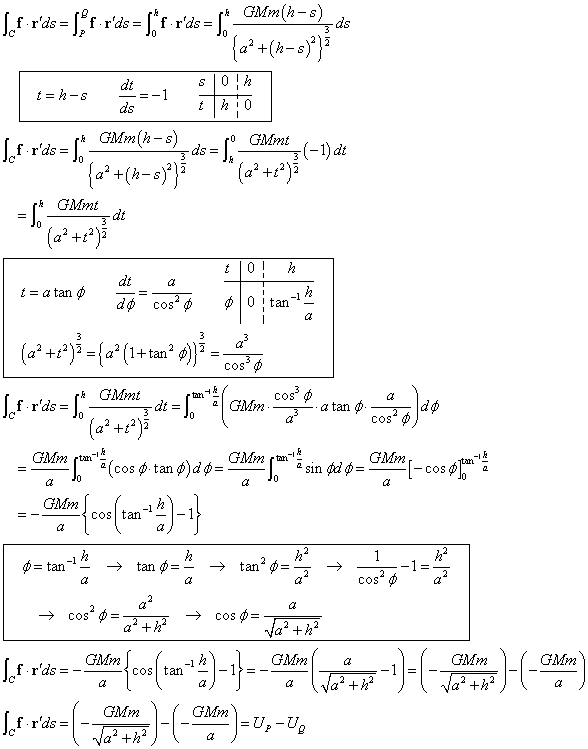
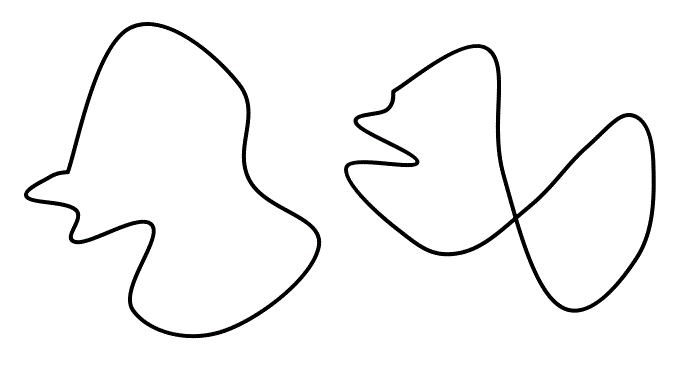
 と、その偏導関数が、CおよびD上で連続であれば、
と、その偏導関数が、CおよびD上で連続であれば、