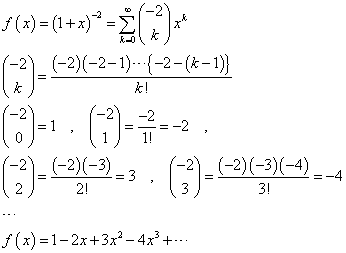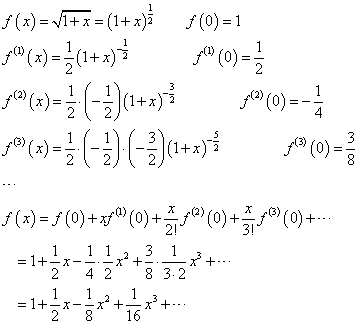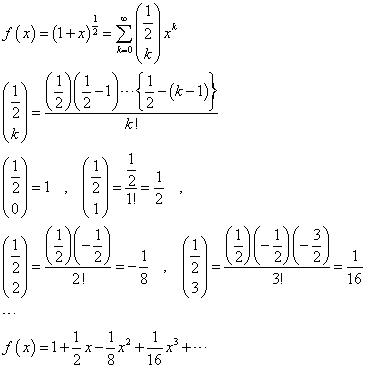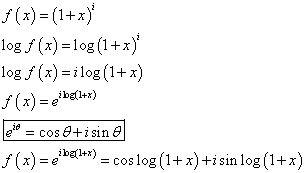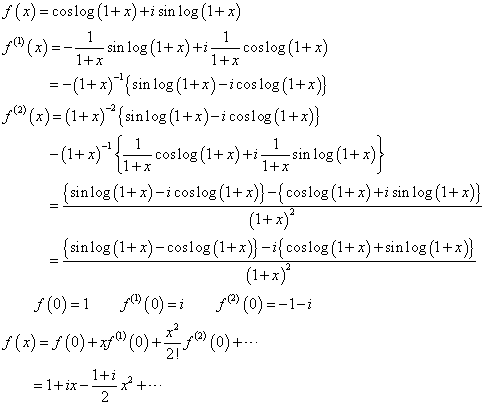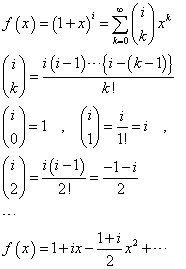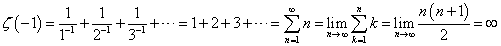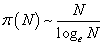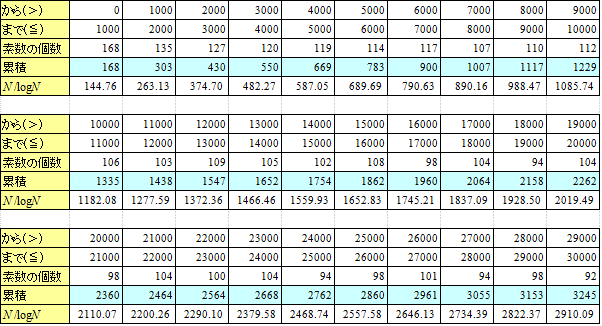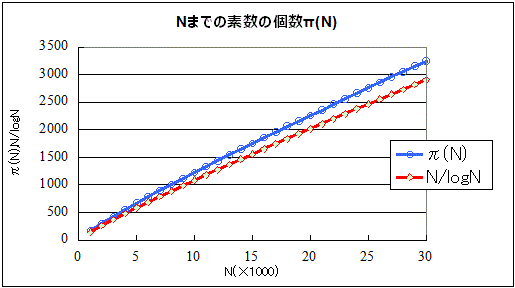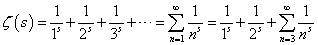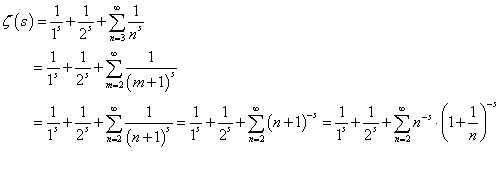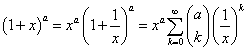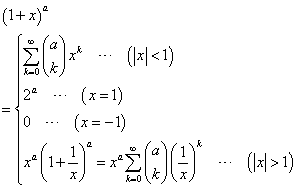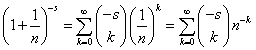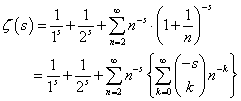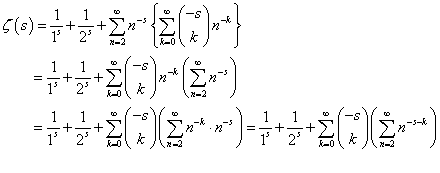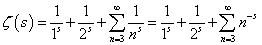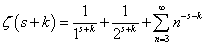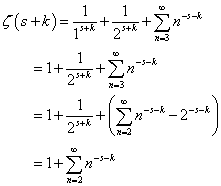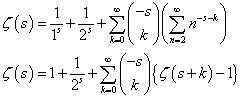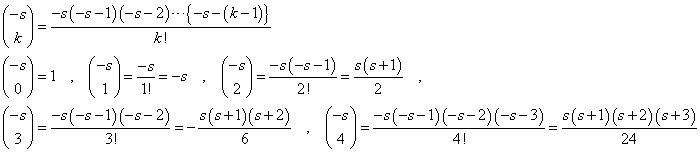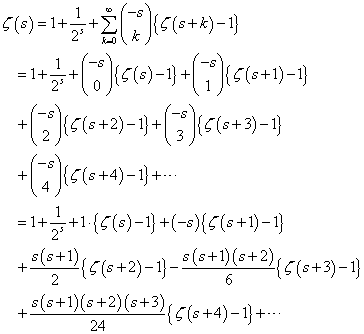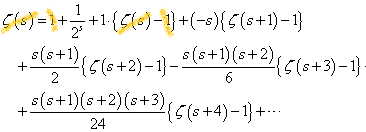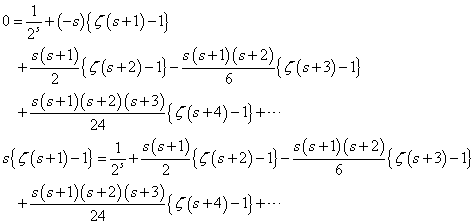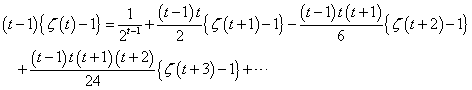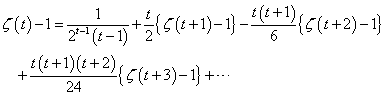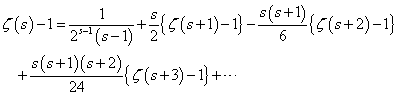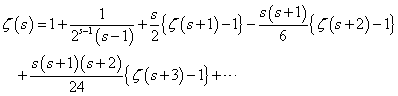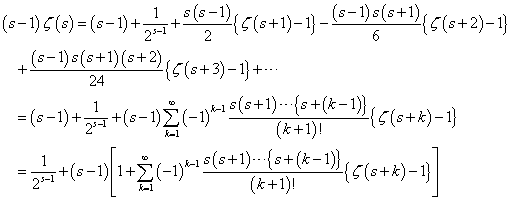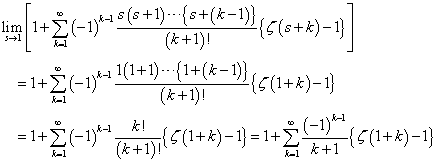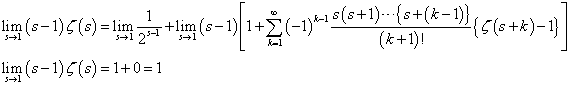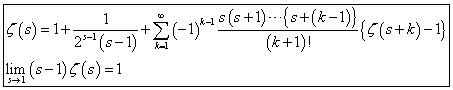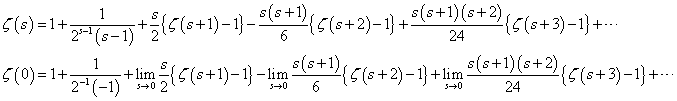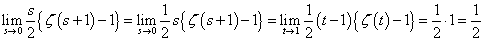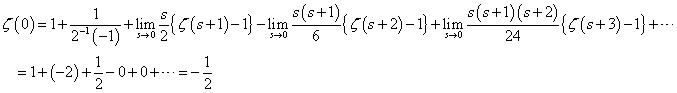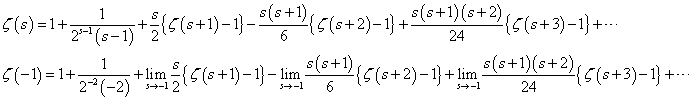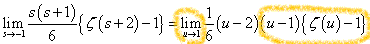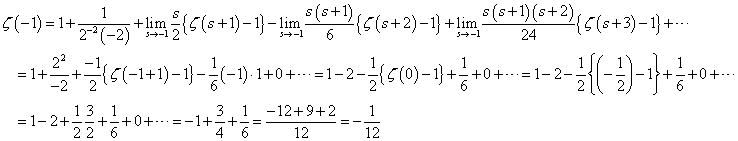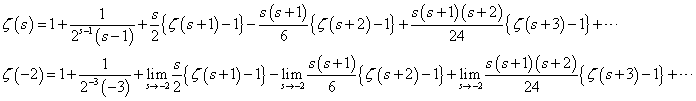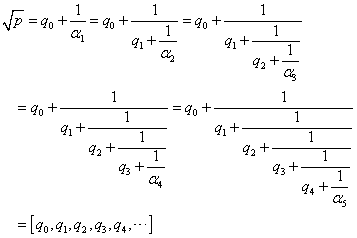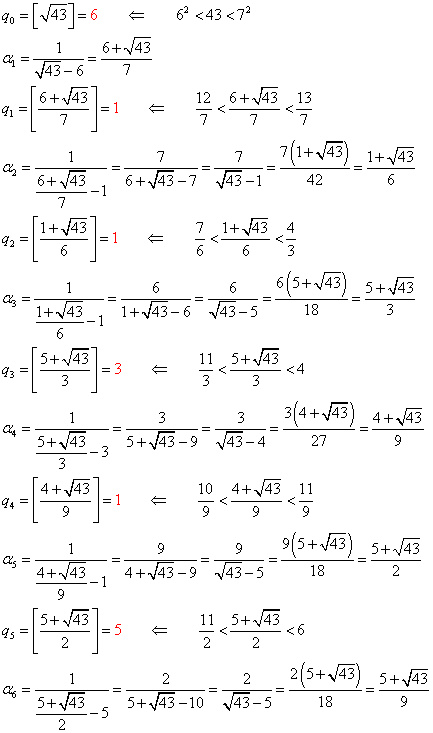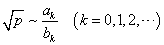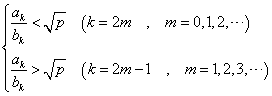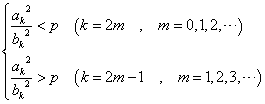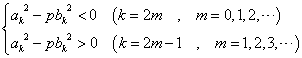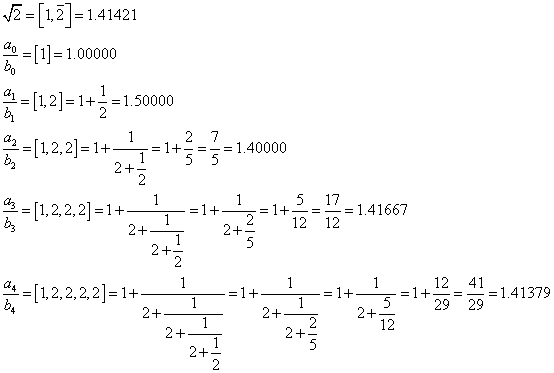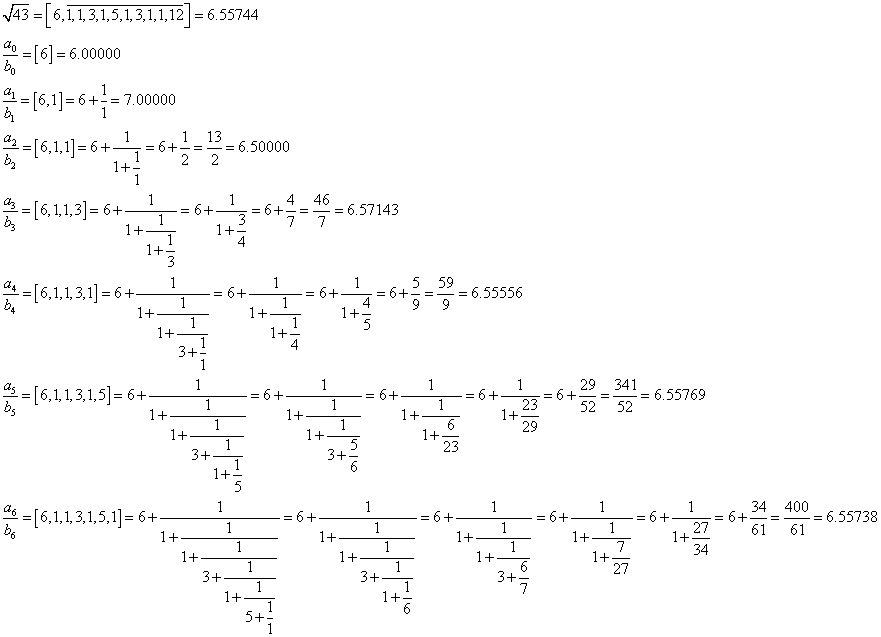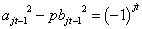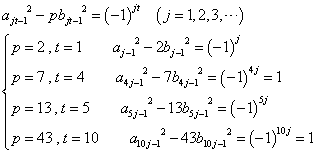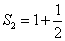
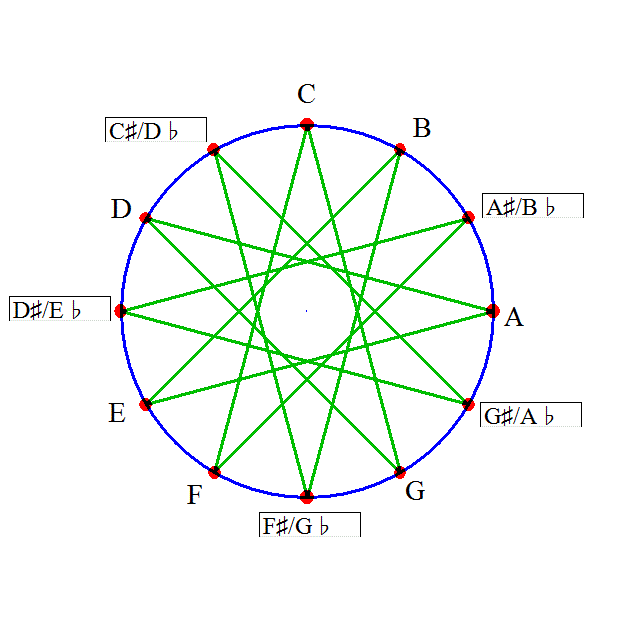
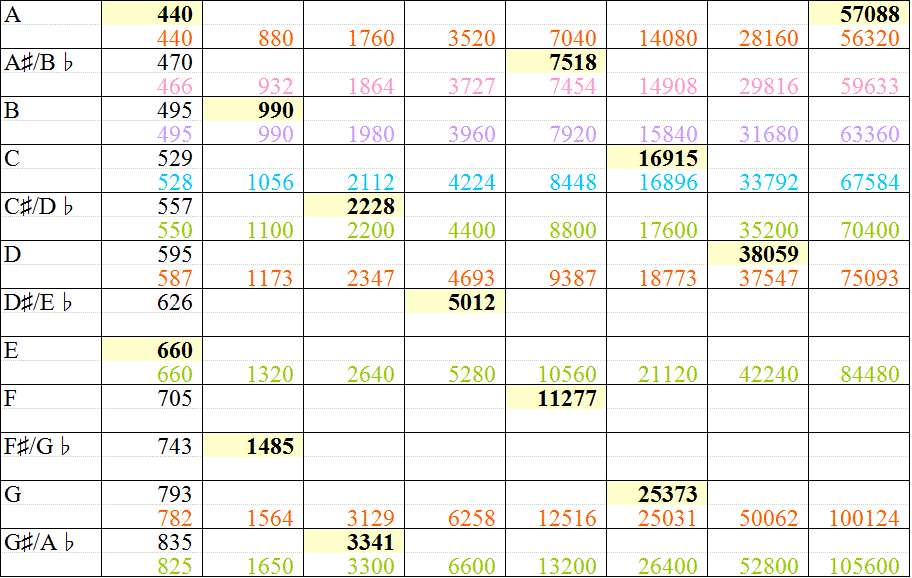
これは、1オクターブ隔たった2音の関係。たとえば、Cと一つ上のC、C0-C1、とでも書こう。
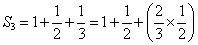
最初の「1」がC0とすると、次の「1/2」は1オクターブ下のC、C-1、その次、「完全5度」下のF-1、そのさらに1オクターブ下だから、C0-C-1-F-2。
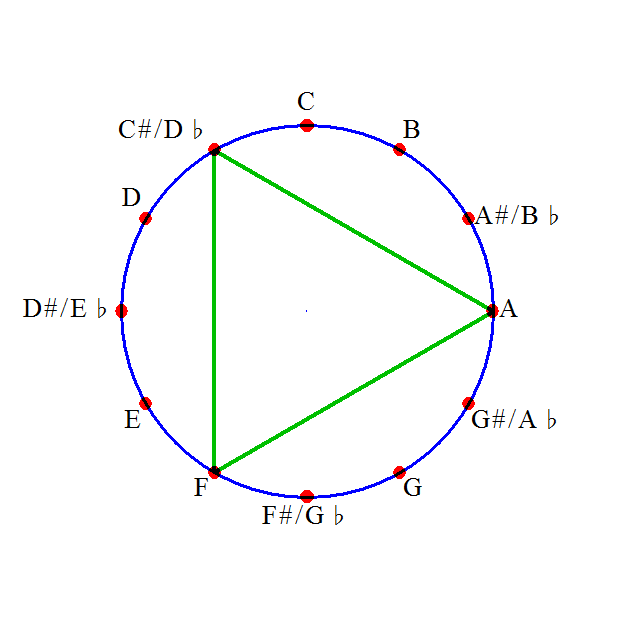
F上に組み立てた「長和音Major_code」F-A-C(ファ・ラ・ド)のラが飛んだと思えばよかろう。
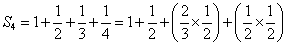
C0-C-1-F-2-C-2、やはり、F-A-C(ファ・ラ・ド)のラが飛んだ。
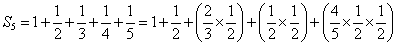
C0-C-1-F-2-C-2、そして最後の項は、C0から「長3度」下がって、G♯-1、その2オクターブ下だから、G♯-3、
「転回形」を作って、F-G♯-Cと並べ直してみると、F-G♯「短3度」、G♯-C「長3度」だから、これは、「短和音minor_code」、F-minorではないか!
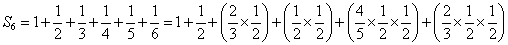
C0-C-1-F-2-C-2-G♯-3、さらに、C0から「完全5度」下がって、F-1、その2オクターブ下だから、F-3、同じく、F-minor。
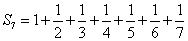
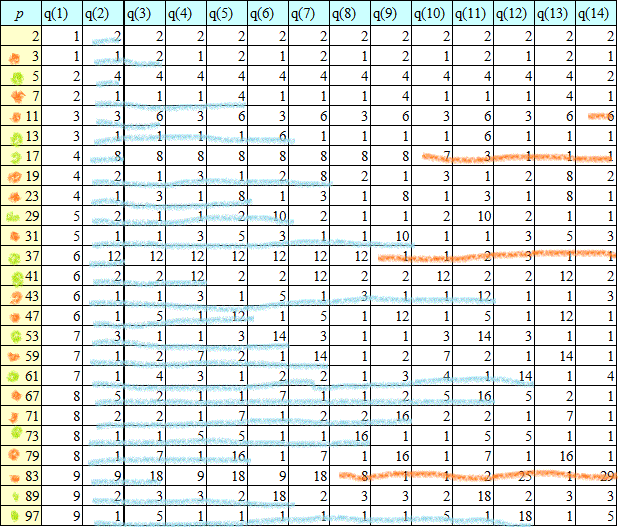
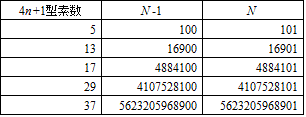
そして、ここで頓挫する。先ほどの「近似値」を見る限り、分子分母に7を素因数として含むものは、見当たらないからな。
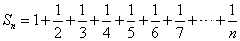
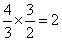
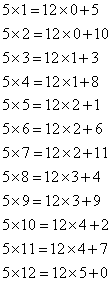
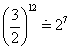
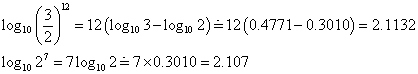
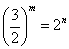
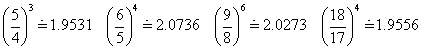
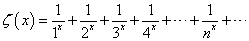

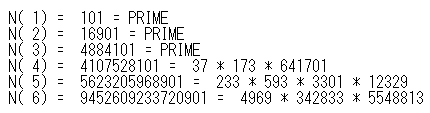
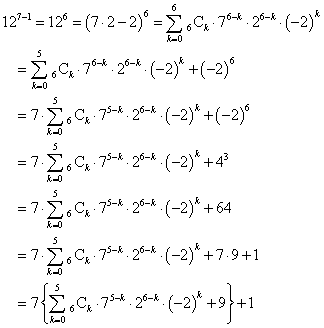
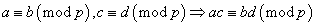
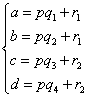

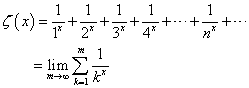
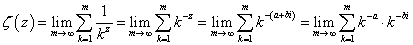
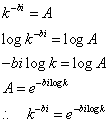
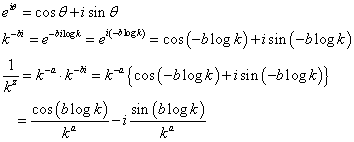
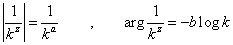
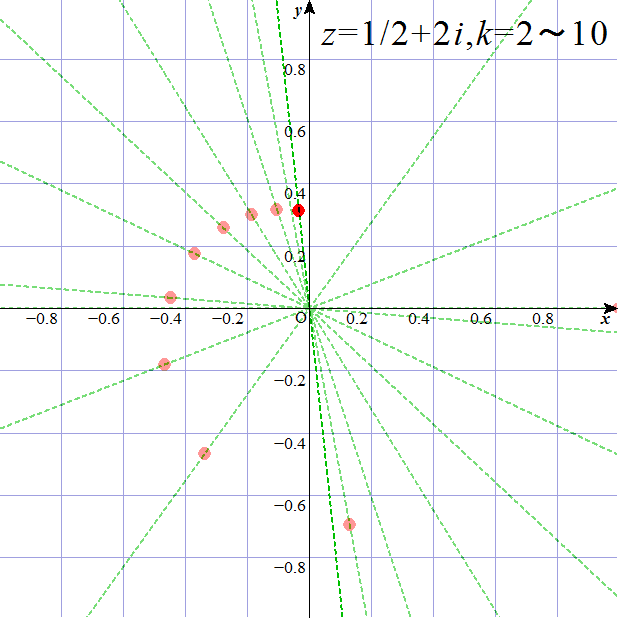
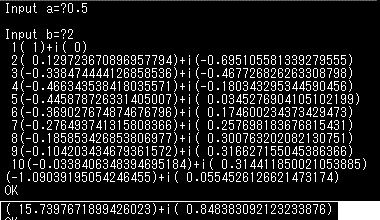
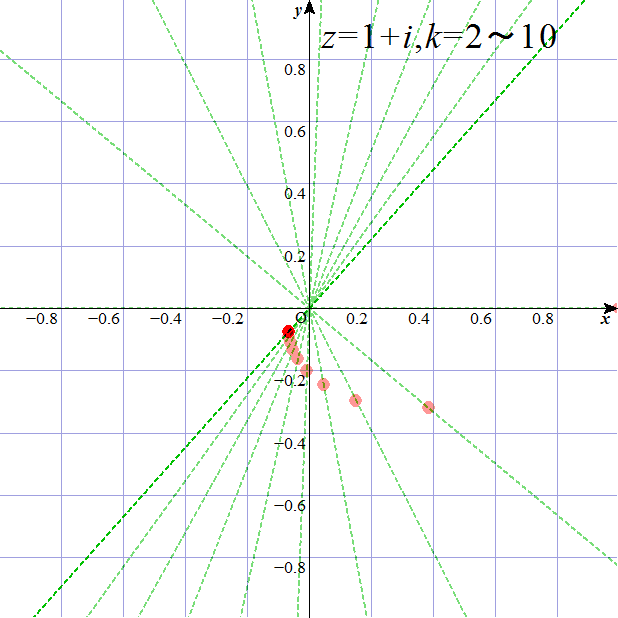

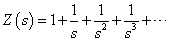
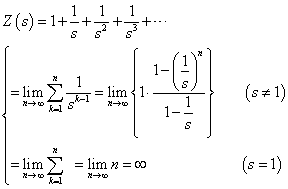
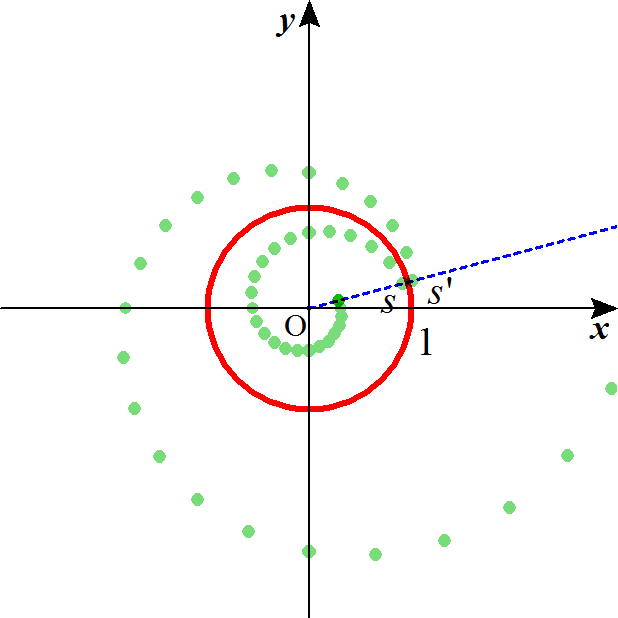
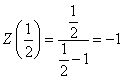


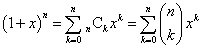
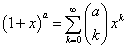
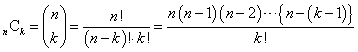

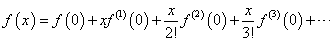
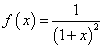 、と、
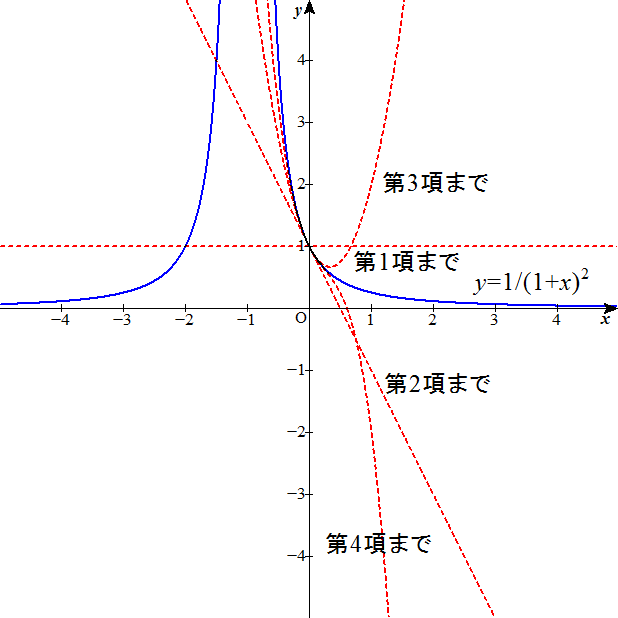
、と、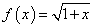 、という二つの関数について、「テイラー展開」と、この「拡張された二項展開」とを、比較してみる。
、という二つの関数について、「テイラー展開」と、この「拡張された二項展開」とを、比較してみる。